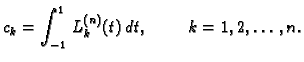



Next: Obične diferencijalne jednadžbe
Up: Numerička matematika
Previous: Rješavanje sustava jednadžbi
Contents
Index
Subsections
Lagrangeov interpolacijski polinom
Neka je dana funkcija
![$ f:[a,b]\rightarrow{}R,$](img2914.gif) i međusobno različite
točke
i međusobno različite
točke
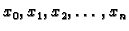 u
u ![$ [a,b].$](img2582.gif) Želimo aproksimirati
funkciju
Želimo aproksimirati
funkciju 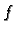 polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija
polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija 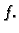 Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše
Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše 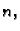 onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
Teorem 27
Neka je dana
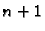
vrijednost
funkcije
![$ f:[a,b]\rightarrow{}R.$](img2918.gif)
Tada
postoji jedan i samo jedan polinom
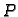
stupnja najviše
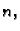
takav
da je
Dokaz. Neka su polinomi
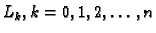 stupnja najviše
stupnja najviše 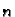 takvi da je
takvi da je
gdje je
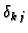 Kroneckerov simbol 1.1. Tada
je
traženi polinom. Doista,
Konstruirajmo sada polinome
Kroneckerov simbol 1.1. Tada
je
traženi polinom. Doista,
Konstruirajmo sada polinome 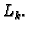 Polinom
Polinom 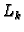 ima nultočke
ima nultočke
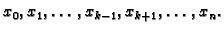 Polinom minimalnog
stupnja s tim svojstvom ima oblik
Broj
Polinom minimalnog
stupnja s tim svojstvom ima oblik
Broj 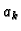 je neodređen. Njega određujemo iz uvjeta
je neodređen. Njega određujemo iz uvjeta
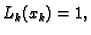 tj.
Tako je
pa je
Dakle
Jedinstvenost ovog polinoma slijedi ovako. Pretpostavimo da je
tj.
Tako je
pa je
Dakle
Jedinstvenost ovog polinoma slijedi ovako. Pretpostavimo da je
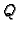 također polinom stupnja najviše
također polinom stupnja najviše 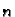 takav da je
takav da je
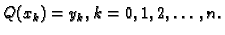 Tada je
Tada je 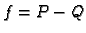 polinom stupnja
najviše
polinom stupnja
najviše 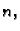 i ima
i ima 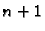 nultočku. Jedna od posljedica Osnovnog
teorema algebre tvrdi da je tada
nultočku. Jedna od posljedica Osnovnog
teorema algebre tvrdi da je tada 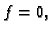 tj.
tj. 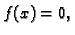 za svaki
za svaki 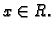 Dakle
Dakle
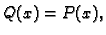 za svaki
za svaki 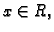 tj.
tj. 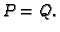
Polinom
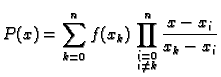 |
(3.13) |
se zove Lagrangeov interpolacijski polinom funkcije 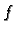 za
točke
za
točke
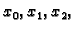
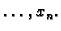
Ocjena greške
Radi jednostavnosti pretpostavimo da je
Iz ovog teorema proizlazi sljedeća ocjena greške. Neka je
Tada za svaki
![$ x\in
[a,b]$](img2669.gif) vrijedi
vrijedi
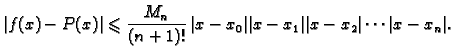 |
(3.16) |
Primjer 3.14
Naći Lagrangeov interpolacioni polinom za funkciju
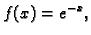
uzimajući da je
zatim pomoću njega naći približnu vrijednost
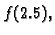
i ocijeniti grešku.
Rješenje. Po formuli (3.13) imamo
Odatle
Ocijenimo sada grešku.
Dakle, prema formuli (
3.16),
greška koju pri tom činimo nije veća od
Metoda najmanjih kvadrata
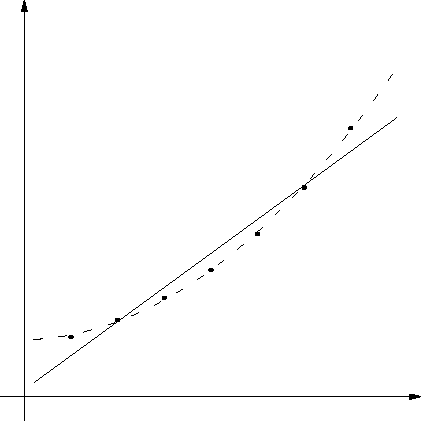
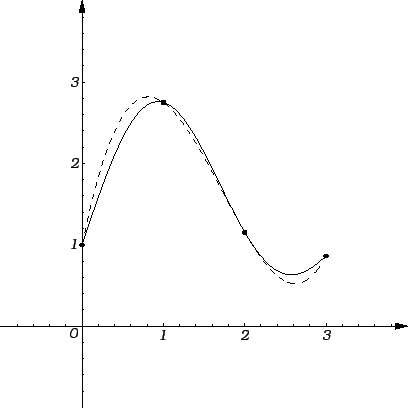
Na sljedećoj slici je funkcija, zadana svojim vrijednostima u
nekoliko točaka, interpolirana polinomom prvog stupnja (pravac) i
polinomom drugog stupnja (crtkana linija) u smislu metode najmanjih
kvadrata.
Lagrangeov polinom veoma dobro aproksimira funkciju lokalno, u
izabranim točkama, dok izvan tih točaka aproksimacija može biti
vrlo loša. Sada ćemo upoznati metodu najmanjih
kvadrata,
metodu pomoću koje možemo zadanu funkciju aproksimirati drugom
funkcijom određenog tipa globalno, tako da u izvjesnom smislu njihova
međusobna udaljenost bude što manja, bez obzira na to što se
funkcije možda neće poklapati niti u jednoj točki.
Pretpostavimo najprije da su vrijednosti funkcije poznate samo u nekim
točkama. Neka su
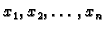 dane točke i neka su
dane točke i neka su
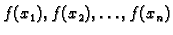 pripadne vrijednosti funkcije
pripadne vrijednosti funkcije 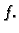 Želimo naći onu funkciju
Želimo naći onu funkciju 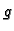 određenog tipa s neodređenim
parametrima
određenog tipa s neodređenim
parametrima
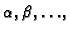 koja najbolje aproksimira
funkciju
koja najbolje aproksimira
funkciju 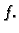 To možemo učiniti na sljedeći način.
To možemo učiniti na sljedeći način.
Izračunamo sumu kvadrata razlika funkcija 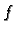 i
i 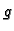
i zatim tražimo neodređene parametre
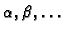 iz
uvjeta da
iz
uvjeta da 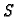 kao funkcija tih parametara ima minimalnu vrijednost.
kao funkcija tih parametara ima minimalnu vrijednost.
Ako je funkcija 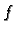 zadana u svim točkama nekog segmenta
zadana u svim točkama nekog segmenta ![$ [a,b],$](img2367.gif) onda se funkcija
onda se funkcija 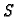 definira pomoću integrala
definira pomoću integrala
Klase funkcija iz kojih biramo funkciju 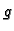 su obično polinomi prvog
stupnja
su obično polinomi prvog
stupnja
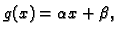 polinomi drugog stupnja
polinomi drugog stupnja
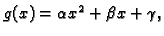 eksponencijalne funkcije
eksponencijalne funkcije
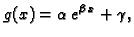 itd.
itd.
Na pr. ako želimo naći polinom prvog stupnja najbliži funkciji
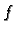 čije su nam vrijednosti poznate u točkama
čije su nam vrijednosti poznate u točkama
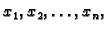 onda je
onda je
![$\displaystyle S(\alpha{},\beta{}) = \sum_{k=1}^n \left[f(x_k) - \alpha{}\,x_k - \beta{}\right]^2.$](img2991.gif) |
(3.17) |
Nužan uvjet za ekstrem funkcije 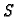 je
dakle
Kad sredimo ovaj sustav jednadžbi, dobijemo
Iz njega izračunamo
je
dakle
Kad sredimo ovaj sustav jednadžbi, dobijemo
Iz njega izračunamo 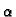 i
i 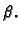 Iz prirode problema jasno
je da funkcija
Iz prirode problema jasno
je da funkcija 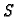 ima samo minimum, pa tako određeni parametri
doista daju najbolju aproksimaciju funkcioje
ima samo minimum, pa tako određeni parametri
doista daju najbolju aproksimaciju funkcioje 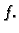
Kad se funkcija 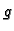 traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
Primjer 3.15
Neka su funkcija i točke kao u primjeru
3.14. Interpolirati funkciju polinomom drugog stupnja, ali metodom najmanjih kvadrata, i pomoću njega približno naći
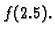
Rješenje. Neka je
polinom koji u smislu metode najmanjih kvadrata interpolira podatke
Sada formulu (
3.17) treba napisati u obliku
Ova funkcija ovisi o tri varijable, pa je nužan uvjet za ekstrem
Kad uvrstimo poznate veličine i sredimo, dobivamo sustav jednadžbi
Rješenje je
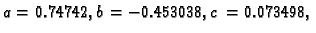
pa je traženi polinom
Tražena vrijednost funkcije je
Numerička integracija
Zadatak je izračunati integral
Umjesto da integriramo podintegralnu funkciju, što često nije
moguće, ili zahtijeva puno posla, integriramo polinom,
koji interpolira funkciju u odgovarajućim točkama.
Numerički to radimo na sljedeći način. Segment ![$ [a,b]$](img2505.gif) podijelimo
na podsegmente točkama
Radi jednostavnosti i
određenosti postupka podjela se uzme ekvidistantnom. U tim točkama
interpoliramo funkciju Lagrangeovim polinomom, i zatim integriramo
polinom. Tako dobiven broj predstavlja približnu vrijednost zadanog
integrala. Dakle
Ako uvrstimo Lagrangeov polinom (3.13), imamo
podijelimo
na podsegmente točkama
Radi jednostavnosti i
određenosti postupka podjela se uzme ekvidistantnom. U tim točkama
interpoliramo funkciju Lagrangeovim polinomom, i zatim integriramo
polinom. Tako dobiven broj predstavlja približnu vrijednost zadanog
integrala. Dakle
Ako uvrstimo Lagrangeov polinom (3.13), imamo
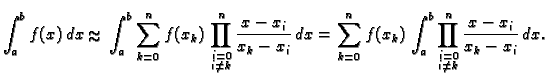 |
(3.18) |
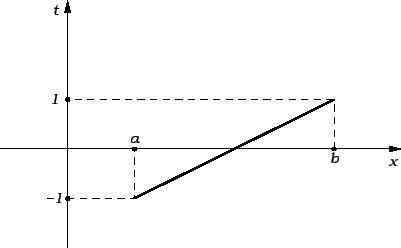
Da bismo razmatranje učinili neovisnim o segmentu ![$ [a,b],$](img2367.gif) svedimo ga
supstitucijom na fiksni segment
svedimo ga
supstitucijom na fiksni segment ![$ [-1,1].$](img3023.gif) To možemo učiniti
afinom funkcijom (polinomom prvog stupnja) čiji je graf pravac kroz
točke
To možemo učiniti
afinom funkcijom (polinomom prvog stupnja) čiji je graf pravac kroz
točke 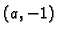 i
i 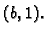 Jednadžba tog pravca je
odnosno
Supstitucija čuva ekvidistantnost, pa je
ekvidistantna podjela segmenta
Jednadžba tog pravca je
odnosno
Supstitucija čuva ekvidistantnost, pa je
ekvidistantna podjela segmenta ![$ [-1,1]$](img3030.gif) na
na 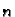 podsegmenata. Tom
supstitucijom formula (3.18) prelazi u
gdje je
podsegmenata. Tom
supstitucijom formula (3.18) prelazi u
gdje je
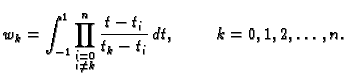 |
(3.19) |
Vidimo da ponderi 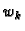 ne
ovise o segmentu, niti o funkciji, već samo o broju
ne
ovise o segmentu, niti o funkciji, već samo o broju 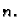
Iz formule (3.14) slijedi da je greška koju pri tom činimo
gdje je
Točka 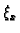 nam nije poznata, pa za ocjenu greške moramo uzeti
maksimum ove derivacije na segmentu
nam nije poznata, pa za ocjenu greške moramo uzeti
maksimum ove derivacije na segmentu ![$ [a,b]$](img2505.gif) gdje je
gdje je
Specijalno za 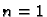 imamo
imamo
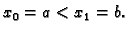 Zatim,
Zatim,
pa je
gdje je
Za 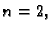 imamo tri točke podjele
imamo tri točke podjele
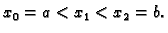 Pretpostavimo da
je podjela ekvidistantna, tj. da je
Pretpostavimo da
je podjela ekvidistantna, tj. da je
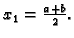 Tada je
Tada je
Kad bismo ponovili
postupak kao gore, dobili bismo ocjenu reda veličine 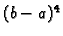 No, ta
se ocjena može poboljšati. Zbog činjenice da je funkcija
No, ta
se ocjena može poboljšati. Zbog činjenice da je funkcija 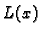 simetrična u odnosu na točku
simetrična u odnosu na točku
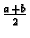 njezin integral po
segmentu
njezin integral po
segmentu ![$ [a,b]$](img2505.gif) iščezava. U tom slučaju se funkcija može
interpolirati s polinomom 4. stupnja, tako da se točka
iščezava. U tom slučaju se funkcija može
interpolirati s polinomom 4. stupnja, tako da se točka
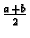 uzme kao dvostruka. O tome kako se to radi ovdje
nećemo govoriti. Primijetimo samo da zbog integriranja polinoma 4.
stupnja ocjena postaje reda veličine
uzme kao dvostruka. O tome kako se to radi ovdje
nećemo govoriti. Primijetimo samo da zbog integriranja polinoma 4.
stupnja ocjena postaje reda veličine 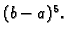 Može se pokazati de
je ona
gdje je
Može se pokazati de
je ona
gdje je
Trapezna formula
U slučaju 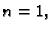 iz formule (3.19) imamo
iz formule (3.19) imamo
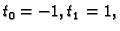 pa su ponderi
pa su ponderi
Prema tome formula glasi
![% latex2html id marker 39864
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{2}\,\left[f(a)+f(b)\right],$](img3053.gif) |
(3.20) |
uz ocjenu greške
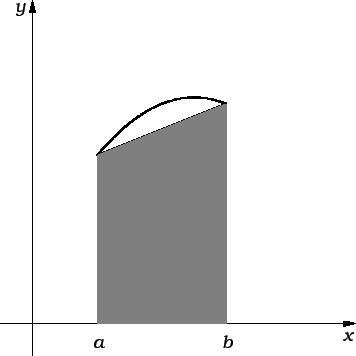
Općenito je greška ove aproksimacije velika. Zato dijelimo segment
![$ [a,b]$](img2505.gif) na podsegmente, i na svakom od njih posebno koristimo ovu
formulu. Radi jednostavnosti uzimamo ekvidistantnu podjelu. Neka je
dakle
na podsegmente, i na svakom od njih posebno koristimo ovu
formulu. Radi jednostavnosti uzimamo ekvidistantnu podjelu. Neka je
dakle
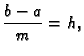
i
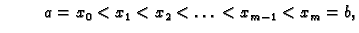
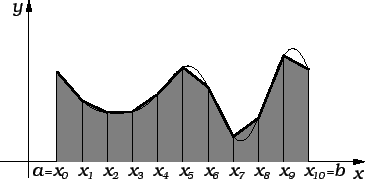
gdje je 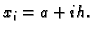 Ako na svaki od podsegmenata, čija je duljina
Ako na svaki od podsegmenata, čija je duljina
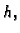 primijenimo formulu (3.20), dobivamo
odnosno
primijenimo formulu (3.20), dobivamo
odnosno
![% latex2html id marker 39880
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{h}...
...eft\{f(a)+2\,\left[f(x_1) + f(x_2) + \cdots{} + f(x_{m-1})\right]+f(b)\right\}.$](img3060.gif) |
(3.21) |
Formula (3.21) se zove trapezna formula.
Ocjena greške se dobije zbrajanjem grešaka na pojedinim
podsegmentima. Tako imamo
gdje je
Za ovu ocjenu trebalo bi mnogo puta (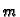 puta) ocjenjivati drugu
derivaciju i to na raznim podsegmentima, što nije jednostavno. Zato
radije ocjenu napravimo jednom za cijeli segment
puta) ocjenjivati drugu
derivaciju i to na raznim podsegmentima, što nije jednostavno. Zato
radije ocjenu napravimo jednom za cijeli segment ![$ [a,b],$](img2367.gif) i uzmemo u
obzir da je za svaki
i uzmemo u
obzir da je za svaki 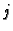 Tako imamo ocjenu
Tako imamo ocjenu
Simpsonova formula
U slučaju 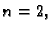 iz formule (3.19) imamo
iz formule (3.19) imamo
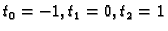 pa su ponderi
pa su ponderi
Prema tome formula glasi
uz ocjenu greške
gdje je
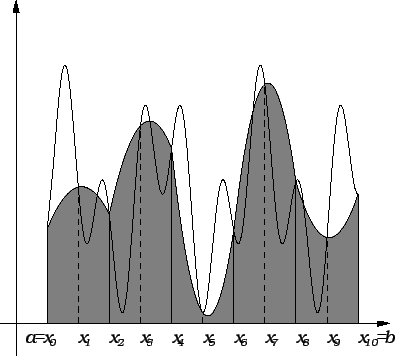
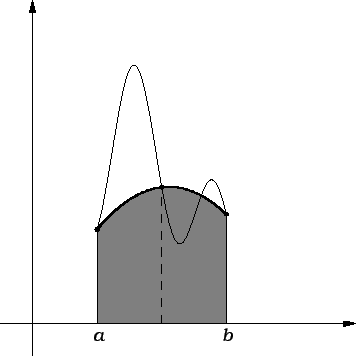
Kao i kod trapezne formule, točniji rezultat ćemo dobiti, ako
segment ![$ [a,b]$](img2505.gif) podijelimo na podsegmente, i na svakom od njih posebno
koristimo ovu formulu. Radi jednostavnosti uzimamo ekvidistantnu
podjelu. Budući da na svakom podsegmentu uzimamo još srednju točku,
podsegmenata imamo zapravo
podijelimo na podsegmente, i na svakom od njih posebno
koristimo ovu formulu. Radi jednostavnosti uzimamo ekvidistantnu
podjelu. Budući da na svakom podsegmentu uzimamo još srednju točku,
podsegmenata imamo zapravo 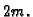 Neka je dakle
Neka je dakle
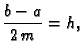
i
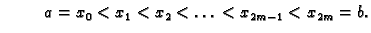
Sada primjenjujemo približnu formulu na parovima susjednih
podsegmenata i to tako da srednja točka bude točka s neparnim
indeksom. Tako dobivamo formulu
odnosno
koja se zove Simpsonova formula.
Diskusija kao kod trapezne formule nas dovodi do ocjene greške
![$\displaystyle \vert R_S\vert \leqslant{} \max_{x\in [a,b]} \left\vert f^{(iv)}(...
...x_{x\in [a,b]} \left\vert f^{(iv)}(x)\right\vert
\,\frac{(b-a)^5}{180\,(2m)^4}.$](img3081.gif)
Primjer 3.16
Pomoću numeričke integracije izračunati približno broj
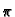
na šest decimala točno.
Rješenje. Najprije sjetimo se da je
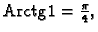 i
i 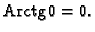 Odatle
Odatle
Dakle
pa treba izračunati ovaj
integral na šest decimala točno. Račun ćemo provesti na dva
načina, pomoću trapezne i pomoću Simpsonove formule.
1. Podintegralna funkcija je
njezina druga derivacija je
a treća
Kako treća derivacija nema nula u
intervalu
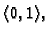
druga derivacija je na tom intervalu
monotona. Računanjem vrijednosti na rubovima lako se vidi da ona raste
i to od
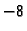
do
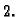
To znači da je
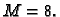
Dakle imamo ocjenu greške
za trapeznu formulu
Budući da tražimo točnost prvih šest decimala, mora biti
tj.
Prema tome treba segment
![$ [0,1]$](img3096.gif)
podijeliti na
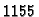
podsegmenata.
2. Pomoću Simpsonove formule račun ide ovako. Četvrta derivacija je
a peta
Peta derivacija se
poništava u
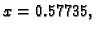
ali je
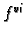
u toj točki pozitivna, pa
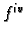
ima u
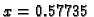
minimum. Tako četvrta derivacija pada na intervalu od 0 do
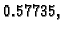
i zatim raste na intervalu od
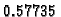
do
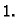
Imamo
Dakle
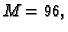
i prema tome treba biti
odakle
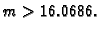
Budući da je broj segmenata potreban za Simpsonovu formulu paran, minimalni
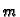
koji treba uzeti je
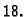
Kad se provede potreban račun dobije se
Trapezna i Simpsonova formula su koristile ekvidistantnu podjelu.
Točke podjele su bile jednoliko razmještene na segmentu. Te formule
u pravilu računaju točno integrale polinoma najviše onog stupnja kojeg je
bio interpolacioni polinom. Tako trapezna formula računa
točno integrale polinoma do uključivo prvog stupnja.
Postavlja se pitanje da li postoje formule koje računaju točno
integrale polinoma stupnja višeg nego što je interpolacioni
polinom. Takve formule postoje i zovu se Gaussove kvadraturne
formule. U tim formulama
točke podjele nisu više ekvidistantno raspoređene. Točke
podjele ćemo u daljnjem zvati čvorovima.
Kvadraturna formula općenito je oblika
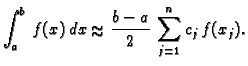 |
(3.22) |
Zbog svojstva linearnosti integrala, kvadraturna formula koja računa
točno potencije do uključivo stupnja 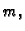 računat će točno i
njihove linearne kombinacije, tj. polinome do uključivo
računat će točno i
njihove linearne kombinacije, tj. polinome do uključivo 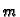 -tog
stupnja. Dakle, pretpostavimo da greška prilikom računanja
potencija do uključivo stupnja
-tog
stupnja. Dakle, pretpostavimo da greška prilikom računanja
potencija do uključivo stupnja 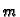 iščezava
Tako imamo
iščezava
Tako imamo 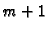 jednadžbu za
jednadžbu za
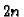 nepoznanica
nepoznanica
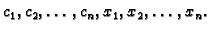 Općenito
sustav treba imati onoliko jednadžbi koliko ima nepoznanica, da bismo
imali jedinstveno rješenje. Ne ulazeći dublje u tu problematiku,
primijetimo da u ovom slučaju to znači da treba biti
Općenito
sustav treba imati onoliko jednadžbi koliko ima nepoznanica, da bismo
imali jedinstveno rješenje. Ne ulazeći dublje u tu problematiku,
primijetimo da u ovom slučaju to znači da treba biti
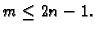 Dakle, u principu, s
Dakle, u principu, s 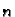 kvadraturnih točaka
kvadraturnih točaka
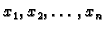 se
mogu rješavati točno integrali polinoma stupnja najviše
se
mogu rješavati točno integrali polinoma stupnja najviše 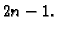
Umjesto rješavanja gornjeg sustava, za određivanje čvorova
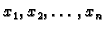 i težina
i težina
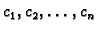 koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
Neprekidne funkcije na ![$ [a,b]$](img2505.gif) čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru
čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru 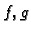 takvih funkcija možemo pridružiti broj
takvih funkcija možemo pridružiti broj
Funkcija, koja uređenom paru 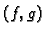 pridružuje
pridružuje
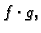 ima
svojstva
ima
svojstva
- 1.
-
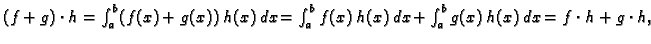
- 2.
-
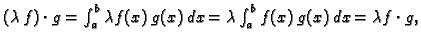
- 3.
-
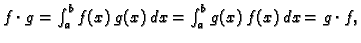
- 4.
-
![$ f\cdot f=\int_a^b [f(x)]^2\,dx \geqslant{} 0,$](img3126.gif)
- 5.
-
![$ f\cdot f=\int_a^b [f(x)]^2\,dx = 0\hspace{1cm}\Leftrightarrow \hspace{1cm}f=0.$](img3127.gif)
pa se zato zove skalarni produkt. To nam omogućava da
govorimo o međusobno ortogonalnim funkcijama, njihovoj duljini itd.
Vratimo se sada na naš problem. Da diskusija ne bi ovisila o
području integracije, prijeđimo na segment ![$ [-1,1]$](img3030.gif) supstitucijom
supstitucijom
Tada je
gdje je
Iz formule (3.22) slijedi
Neka su
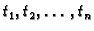 tražene kvadraturne točke. Po
pretpostavci, kvadraturna formula je točna za polinome do uključivo
tražene kvadraturne točke. Po
pretpostavci, kvadraturna formula je točna za polinome do uključivo
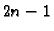 -og stupnja. Prema tome
za
-og stupnja. Prema tome
za
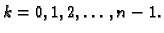 S druge strane suma iščezava, jer se za svaki
S druge strane suma iščezava, jer se za svaki
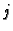 jedan faktor poništava. To znači, da je polinom
okomit na polinome
jedan faktor poništava. To znači, da je polinom
okomit na polinome
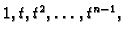 a prema tome i na njihove
linearne kombinacije, tj. na sve polinome stupnja najviše
a prema tome i na njihove
linearne kombinacije, tj. na sve polinome stupnja najviše 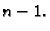 Takvi polinomi se
zovu Legendreovi polinomi. Točke Gaussove kvadrature su upravo
korijeni (nule) tih polinoma. Nađimo Legendreove polinome. U tu svrhu
ortogonalizirajmo polinome
Takvi polinomi se
zovu Legendreovi polinomi. Točke Gaussove kvadrature su upravo
korijeni (nule) tih polinoma. Nađimo Legendreove polinome. U tu svrhu
ortogonalizirajmo polinome
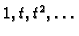 Gram-Schmidtovim postupkom
Gram-Schmidtovim postupkom
Tako na segmentu ![$ [-1,1]$](img3030.gif) imamo točke kvadrature
imamo točke kvadrature
Težine 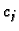 jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
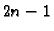 -og stupnja. Neka su
-og stupnja. Neka su
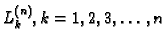 polinomi sa
svojstvom
polinomi sa
svojstvom
To su
polinomi koji su se pojavili prilikom Lagrangeove interpolacije.
Njihov stupanj je 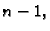 pa Gaussova kvadratura računa njihove
integrale točno. To znači
tj.
pa Gaussova kvadratura računa njihove
integrale točno. To znači
tj.
Nultočke Legendreovihovih polinoma uglavnom su iracionalni
brojevi, pa uzimajući vrijednosti iz gornje tablice, činimo grešku
zamjenjujući iracionalan broj decimalnim. Tako ipak ne dobivamo
apsolutnu točnost. No, barem smo uklonili grešku koja se odnosi na
zamjenu integrala kvadraturnom formulom.




Next: Obične diferencijalne jednadžbe
Up: Numerička matematika
Previous: Rješavanje sustava jednadžbi
Contents
Index
Salih Suljagic
1999-12-17
![]() i međusobno različite
točke
i međusobno različite
točke
![]() u
u ![]() Želimo aproksimirati
funkciju
Želimo aproksimirati
funkciju ![]() polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija
polinomom koji u izabranim točkama ima iste vrijednosti
kao funkcija ![]() Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše
Ovako postavljen problem ima mnogo rješenja.
Međutim, ako zahtijevamo da stupanj polinoma bude najviše ![]() onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
onda
imamo samo jedno rješenje, što upravo tvrdi sljedeći teorem.
![]() stupnja najviše
stupnja najviše ![]() takvi da je
takvi da je
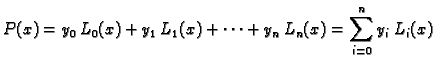
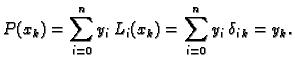
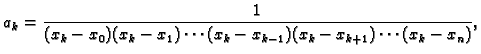
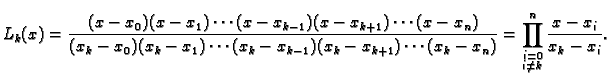
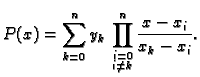
![]() za neki
za neki ![]() onda nemamo što dokazivati, jer su tada obje strane u
(3.14) jednake nuli. Zato pretpostavimo da je
onda nemamo što dokazivati, jer su tada obje strane u
(3.14) jednake nuli. Zato pretpostavimo da je
![]() i
i
![]() za svaki
za svaki ![]() Stavimo, radi kraćeg
zapisa
Stavimo, radi kraćeg
zapisa
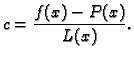
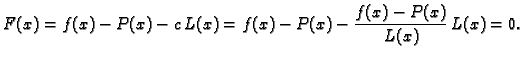
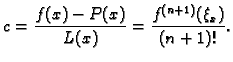
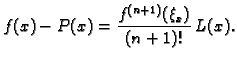
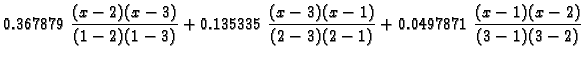
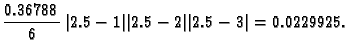
![]() dane točke i neka su
dane točke i neka su
![]() pripadne vrijednosti funkcije
pripadne vrijednosti funkcije ![]() Želimo naći onu funkciju
Želimo naći onu funkciju ![]() određenog tipa s neodređenim
parametrima
određenog tipa s neodređenim
parametrima
![]() koja najbolje aproksimira
funkciju
koja najbolje aproksimira
funkciju ![]() To možemo učiniti na sljedeći način.
To možemo učiniti na sljedeći način.
![]() i
i ![]()
![$\displaystyle S = \sum_{k=1}^n \left[f(x_k) - g(x_k)\right]^2,$](img2984.gif)
![]() zadana u svim točkama nekog segmenta
zadana u svim točkama nekog segmenta ![]() onda se funkcija
onda se funkcija ![]() definira pomoću integrala
definira pomoću integrala
![$\displaystyle S = \int_{a}^b \left[f(x) - g(x)\right]^2\,dx.$](img2986.gif)
![]() su obično polinomi prvog
stupnja
su obično polinomi prvog
stupnja
![]() polinomi drugog stupnja
polinomi drugog stupnja
![]() eksponencijalne funkcije
eksponencijalne funkcije
![]() itd.
itd.
![]() čije su nam vrijednosti poznate u točkama
čije su nam vrijednosti poznate u točkama
![]() onda je
onda je
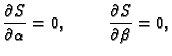
![$\displaystyle \sum_{k=1}^n \left[f(x_k) - \alpha{}\,x_k - \beta{}\right]\,x_k =
0,$](img2993.gif)
![$\displaystyle \sum_{k=1}^n \left[f(x_k) - \alpha{}\,x_k - \beta{}\right] = 0.$](img2994.gif)
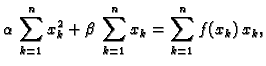
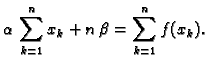
![]() traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
traži u obliku eksponencijalne, logaritamske i
slično, onda se na ovaj način u pravilu dobije sustav nelinearnih
jednadžbi. Takve sustave je teže rješavati nego linearne. Obično
se nekim operacijama nad funkcijama (na pr. logaritmiranjem)
pojednostavni klasa funkcija u kojoj tražimo aproksimaciju. No,
parametri koje tako dobijemo nisu najbolji mogući u smislu metode
najmanjih kvadrata.
![$\displaystyle S(a,b,c) = \sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]^2.$](img3003.gif)
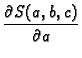
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right] = 0$](img3005.gif)
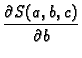
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]\,x_k = 0$](img3007.gif)
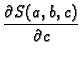
![$\displaystyle -2\,\sum_{k=1}^3 \left[f(x_k) -
c\,x^2 - b\,x_k - a\right]\,x_k^2 = 0.$](img3009.gif)
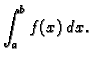
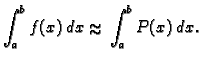
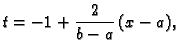
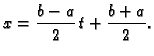
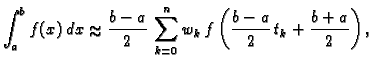
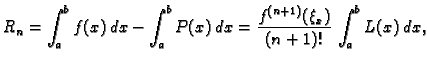
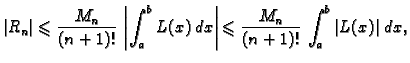
![]() imamo
imamo
![]() Zatim,
Zatim,
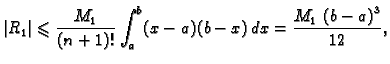
![]() imamo tri točke podjele
imamo tri točke podjele
![]() Pretpostavimo da
je podjela ekvidistantna, tj. da je
Pretpostavimo da
je podjela ekvidistantna, tj. da je
![]() Tada je
Tada je
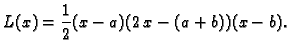
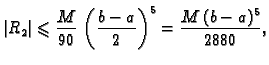
![]() iz formule (3.19) imamo
iz formule (3.19) imamo
![]() pa su ponderi
pa su ponderi
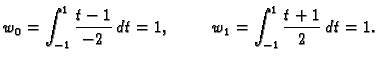
![$\displaystyle \vert R_1\vert \leqslant{} \max_{x\in [a,b]}
\left\vert f''(x)\right\vert\frac{(b-a)^3}{12}.$](img3054.gif)
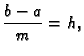 i
i ![% latex2html id marker 39878
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{h}...
...ft[f(x_1)+f(x_2)\right] + \cdots{} +
\frac{h}{2}\,\left[f(x_{m-1})+f(b)\right],$](img3059.gif)
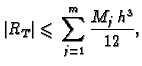
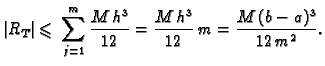
![]() iz formule (3.19) imamo
iz formule (3.19) imamo
![]() pa su ponderi
pa su ponderi
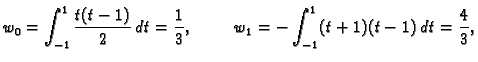
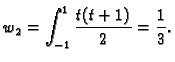
![% latex2html id marker 39906
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{6}\,\left[f(a) +
4\, f\left(\frac{a+b}{2}\right) + f(b)\right],$](img3069.gif)
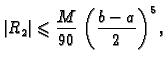
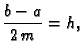 i
i ![% latex2html id marker 39920
$\displaystyle \int_a^b f(x)\,dx \approx{} \frac{b-a}{6\,m}\,\left[f(a) +
4\, f(x_1) + f(x_2)\right]+$](img3075.gif)
![$\displaystyle + \frac{b-a}{6\,m}\,\left[f(x_2) +
4\, f(x_3) + f(x_4)\right] + \cdots{}+$](img3076.gif)
![$\displaystyle +
\frac{b-a}{6\,m}\,\left[f(x_{2m-2}) +
4\, f(x_{2m-1}) + f(x_{b})\right],$](img3077.gif)
![% latex2html id marker 39926
$\displaystyle \int_a^b f(x)\,dx\approx\frac{h}{3}\{f(a)+2\,[f(x_2)+f(x_4)+\cdots
+f(x_{2m-2})]$](img3078.gif)

![$\displaystyle \vert R_S\vert \leqslant{} \max_{x\in [a,b]} \left\vert f^{(iv)}(...
...x_{x\in [a,b]} \left\vert f^{(iv)}(x)\right\vert
\,\frac{(b-a)^5}{180\,(2m)^4}.$](img3081.gif)
![]() i
i ![]() Odatle
Odatle
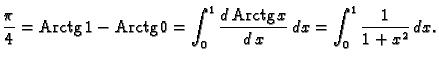
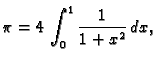
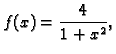
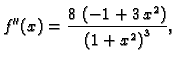
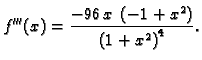
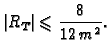
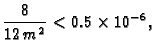
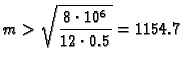
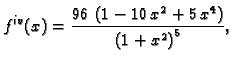
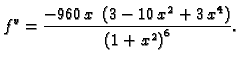
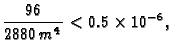
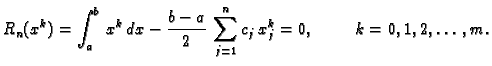
![]() i težina
i težina
![]() koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
koristimo ideju
koja potječe od C. F. Gaussa, a osniva se na sljedećem
razmatranju.
![]() čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru
čine vektorski prostor obzirom na
uobičajene operacije zbrajanja funkcija i množenja funkcije
brojem. Svakom paru ![]() takvih funkcija možemo pridružiti broj
takvih funkcija možemo pridružiti broj
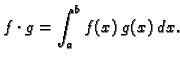
![]() supstitucijom
supstitucijom
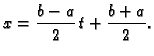
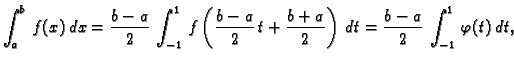
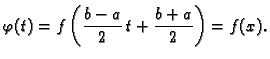
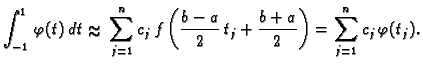
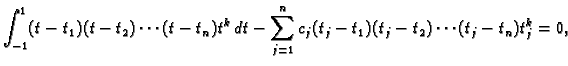
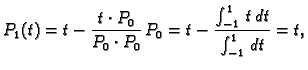
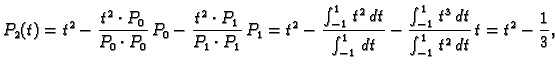
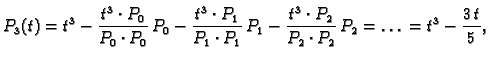
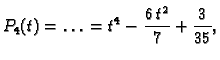
![]() imamo točke kvadrature
imamo točke kvadrature
![]() jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
jednostavno možemo izračunati na sljedeći
način. Gaussova kvadratura računa točno polinome do uključivo
![]() -og stupnja. Neka su
-og stupnja. Neka su
![]() polinomi sa
svojstvom
polinomi sa
svojstvom