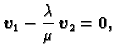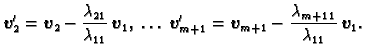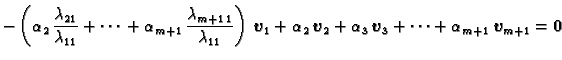



Next: Sustavi linearnih algebarskih jednadžbi
Up: Matrice i sustavi jednadžbi
Previous: Matrice i sustavi jednadžbi
Contents
Index
Subsections
Matricu ćemo kraće zapisivati ovako
Operacije s matricama
Za dvije matrice
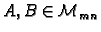
kažemo da su jednake ako je
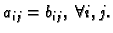
Zbrajati možemo samo matrice istog tipa.
Neka su
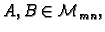
Zbroj 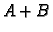 je matrica tipa
je matrica tipa 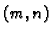
Umnožak matrice
![$ A=[a_{ij}]$](img62.gif) i broja
i broja 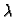 je matrica
je matrica 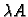 istog tipa kao i
istog tipa kao i 
Zbog svojstava zbrajanja i množenja brojeva, operacije zbrajanja
matrica i množenja matrice brojem očito
imaju sljedeća svojstva.
- 1.
-
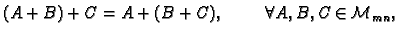
- 2.
-
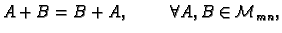
- 3.
- Postoji
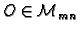 takav da je
takav da je
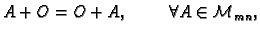
(To je matrica ![$ O=[0],$](img70.gif) tj.
tj. 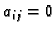 za svaki
za svaki 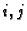 ),
),
- 4.
-
 postoji
postoji
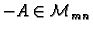 takav da je
takav da je
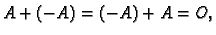
(To je matrica
![$ -A=[-a_{ij}]$](img76.gif) ),
),
- 5.
-
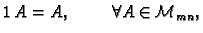
- 6.
-

- 7.
-

- 8.
-
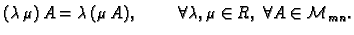
S obzirom na to da su u skupu
 dane dvije operacije, zbrajanje i
množenje brojem, i da te operacije imaju navedenih osam svojstva,
skup
dane dvije operacije, zbrajanje i
množenje brojem, i da te operacije imaju navedenih osam svojstva,
skup
 zovemo vektorskim
prostorom.
zovemo vektorskim
prostorom.
Matrica
![$ A=[a_{ij}]$](img62.gif) tipa
tipa 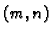 i matrica
i matrica
![$ B=[b_{lk}]$](img81.gif) tipa
tipa 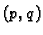 se mogu pomnožiti tim redom samo ako je
se mogu pomnožiti tim redom samo ako je
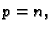 tj. ako je broj stupaca prve matrice jednak broju redaka druge
matrice. U tom slučaju možemo indeks
tj. ako je broj stupaca prve matrice jednak broju redaka druge
matrice. U tom slučaju možemo indeks 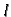 zamijeniti s
zamijeniti s 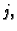 pa je
pa je
Produkt 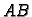 je matrica tipa
je matrica tipa 
Množenje matrica ima ova svojstva.
- 1.
-
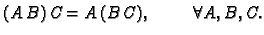
- 2.
-
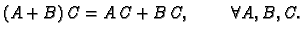
- 3.
-
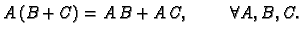
- 4.
- Postoji kvadratna matrica odgovarajućeg reda
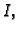 takva da je
takva da je
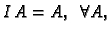 i također kvadratna matrica odgovarajućeg
reda
i također kvadratna matrica odgovarajućeg
reda 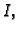 takva da je
takva da je
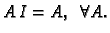
Matrica 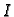 se zove
jedinična matrica. Njezini elementi su
se zove
jedinična matrica. Njezini elementi su 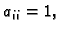 za svaki
za svaki 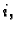 te
te 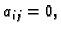 za
za 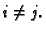 Pomoću Kroneckerovog
simbola
Pomoću Kroneckerovog
simbola
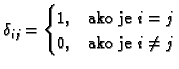 |
(1.1) |
možemo kratko zapisati jediničnu matricu kao
Produkt nije komutativan, tj. ne vrijedi općenito
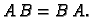 Naime, kod produkta
Naime, kod produkta 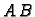 je nužno da broj stupaca matrice
je nužno da broj stupaca matrice  bude
jednak broju redaka matrice
bude
jednak broju redaka matrice 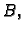 dok je u produktu
dok je u produktu 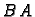 nužno da
broj redaka matrice
nužno da
broj redaka matrice  bude jednak broju stupaca matrice
bude jednak broju stupaca matrice 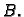 Tako se
može dogoditi da jedan produkt postoji, a drugi ne.
Tako se
može dogoditi da jedan produkt postoji, a drugi ne.
Neka je dana matrica  tipa
tipa 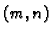
Matrica, koja se iz  dobije kad reci postanu stupci,
označava se sa
dobije kad reci postanu stupci,
označava se sa 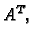 ona je tipa
ona je tipa 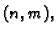 i zove se
transponirana matrica matrice
i zove se
transponirana matrica matrice 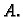 Dakle,
Transponiranje se prema operacijama s matricama odnosi kako slijedi.
Dakle,
Transponiranje se prema operacijama s matricama odnosi kako slijedi.
- 1.
-
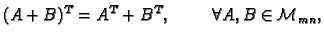
- 2.
-
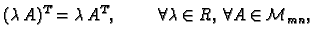
- 3.
-
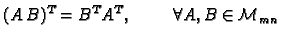
- 4.
-

Operacije, koje su dane u
 omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
omogućavaju da pravimo linearne
kombinacije matrica. Neka su dane matrice
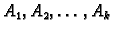 istog
tipa, i brojevi
istog
tipa, i brojevi
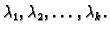 Linearnom kombinacijom matrica
Linearnom kombinacijom matrica
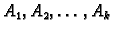 zovemo matricu
zovemo matricu
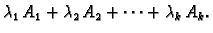 |
(1.2) |
Brojeve
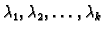 zovemo
koeficijentima linearne kombinacije
(1.2).
zovemo
koeficijentima linearne kombinacije
(1.2).
Definicija 2
Za matrice
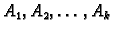
kažemo da su
linearno nezavisne, ako
U protivnom kažemo da su
linearno zavisne.
Definicija 3
U kvadratnoj matrici
![$ A=[a_{ij}]$](img62.gif)
reda

elementi
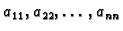
čine
glavnu
dijagonalu.
Zbroj elemenata na glavnoj dijagonali kvadratne matrice zovemo
trag
matrice i pišemo
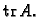
Dakle,
Kvadratne matrice imaju redaka koliko i stupaca, pa
se mogu množiti u bilo kojem poretku, no i u tom slučaju produkt nije
komutativan kao što pokazuje sljedeći primjer.
Definicija 4
Neka je

kvadratna matrica. Matrica

se zove
- -
- dijagonalna
matrica, ako je
![$ A=[a_{ij}\,\delta_{ij}],$](img130.gif) tj. ako su joj
elementi izvan glavne dijagonale jednaki nuli,
tj. ako su joj
elementi izvan glavne dijagonale jednaki nuli,
- -
- skalarna
matrica, ako je
![$ A=[a\,\delta_{ij}],$](img131.gif) tj. ako je dijagonalna i
ako su joj elementi na glavnoj dijagonali međusobno jednaki,
tj. ako je dijagonalna i
ako su joj elementi na glavnoj dijagonali međusobno jednaki,
- -
- gornja trokutasta, ako su joj
elementi ispod glavne dijagonale jednaki nuli,
- -
- donja trokutasta, ako su joj elementi iznad glavne
dijagonale jednaki nuli.
Skalarna matrica je dijagonalna, dok obrat naravno ne
vrijedi. Nulmatrica 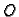 i jedinična matrica
i jedinična matrica 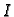 su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
su skalarne
matrice. Dapače, svaka skalarna matrica ima oblik
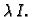
Budući da je 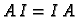 za svaku kvadratnu matricu
za svaku kvadratnu matricu 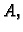 bilo koja
skalarna matrica komutira sa svakom matricom
bilo koja
skalarna matrica komutira sa svakom matricom
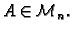
Elementi na glavnoj dijagonali
antisimetrične matrice su nule. Svaka kvadratna matrica se može na
jedinstven način razložiti na zbroj simetrične i antisimetrične
marice:
Da je 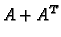 simetrična, a
simetrična, a 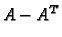 antisimetrična matrica, lako se
vidi upotrebom gornjih svojstava.1.1.1
antisimetrična matrica, lako se
vidi upotrebom gornjih svojstava.1.1.1
Determinanta
Definicija 6
Neka je dana kvadratna matrica
![$ A=\left[a_{ij}\right]$](img143.gif)
reda
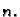 Determinantom
Determinantom matrice

zovemo broj
gdje je
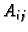
determinanta one matrice
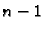
-og reda koja se dobije
kad se u matrici

prekriže
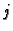
-ti redak i
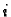
-ti stupac,
pomnožena s
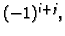
tj.
Broj
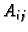
se zove
algebarski
komplement matričnog elementa
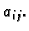
Determinantu matrice reda

ćemo kraće zvati
determinantom  -tog reda.
-tog reda.
Ova definicija svodi računanje determinanti  -tog reda na
računanje determinanti
-tog reda na
računanje determinanti 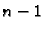 -og reda, ovih opet po istoj formuli na
računanje determinanti
-og reda, ovih opet po istoj formuli na
računanje determinanti 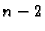 -og reda, itd. Tako dolazimo na kraju do
determinanti trećeg ili drugog reda koje znamo izračunati
-og reda, itd. Tako dolazimo na kraju do
determinanti trećeg ili drugog reda koje znamo izračunati
Računanje determinante po ovoj formuli je nepraktično, jer se s
povećanjem reda jako povećava broj determinanti drugog ili trećeg
reda koje treba izračunati. Zato ćemo navesti neka svojstva
determinanti koja mogu bitno pojednostavniti njihovo računanje.
- 1.
- Ako su svi elementi nekog retka ili stupca nule, onda je determinanta
jednaka nuli.
- 2.
- Ako su ispod ili iznad glavne dijagonale nule, onda je determinanta
jednaka produktu brojeva na glavnoj dijagonali.
- 3.
- Ako dva stupca ili dva retka zamijene mjesta, onda determinanta mijenja
znak.
- 4.
- Ako su dva stupca ili dva retka jednaka, onda je determinanta
jednaka nuli.
- 5.
- Ako nekom stupcu ili retku dodamo linearnu kombinaciju preostalih
stupaca ili redaka, onda se determinanta ne mijenja.
- 6.
- Determinanta se množi brojem tako da se neki redak ili stupac
pomnoži tim brojem.
- 7.
- (Binet-Cauchyjev
teorem) Determinanta produkta dvije matrice jednaka je produktu
determinanti, tj.
- 8.
- Ako je neki stupac ili redak linearna kombinacija preostalih
stupaca ili redaka, onda je determinanta jednaka nuli.
- 9.
-
Primjer 1.2
Riješite jednadžbu
Rješenje. Da se vidi o kojoj algebarskoj jednadžbi se radi, treba
izračunati determinantu. Umjesto računanja determinante po
definiciji, jednostavnije je koristiti svojstva
determinante. Množenjem prvog retka s 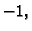 i dodavanjem drugom,
trećem i četvrtom retku, dobivamo
i dodavanjem drugom,
trećem i četvrtom retku, dobivamo
Da izbjegnemo minuse pomnožimo drugi, treći i četvrti redak s
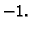
Time se promijeni predznak determinante, ali kako se radi o jednadžbi
u kojoj je na desnoj strani
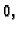
to nema utjecaja na rezultat. Zatim
nastavimo slično s drugim, trećim i četvrtim retkom sa svrhom da
ispod glavne dijagonale dobijemo nule, kako bismo je po svojstvu
2 lako izračunali . Na kraju dobivamo
Prema tome jednadžba je
i rješenje je
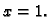
Definicija 7
Neka je dana matrica
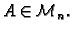
Matrica
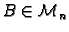
sa svojstvom
se zove
inverzna matrica
matrice
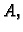
i piše se
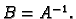
Kvadratna matrica, koja ima inverznu, se zove
regularna.
Kvadratna matrica, koja nema inverznu, se zove
singularna.
Teorem 1
Inverzna matrica, ukoliko postoji, jedinstvena je.
Dokaz. Neka je
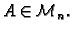 Pretpostavimo da su
Pretpostavimo da su 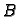 i
i 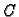 njoj inverzne matrice. Tada je
njoj inverzne matrice. Tada je
Pomnožimo ovu jednakost s desne strane s 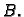 Dobivamo
Dakle,
Dobivamo
Dakle, 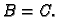
Svojstva skupa regularnih matrica.
- 1.
- Produkt regularnih matrica je regularna matrica i vrijedi
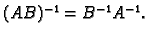
- 2.
- Jedinična matrica
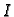 je regularna, i
je regularna, i 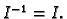
- 3.
-
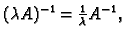 za svaki
za svaki
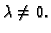
- 4.
-
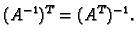
- 5.
-
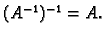
- 6.
- Ako je
 regularna matrica, onda je
regularna matrica, onda je
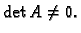
Nulmatrica množena s bilo kojom matricom daje nulmatricu,
pa tako ne postoji njezin inverz. Dakle, nulmatrica je singularna. No
to nije jedina singularna matrica kao što pokazuje sljedeći primjer.
Primjer 1.3
Matrica
nema inverznu.
Rješenje. Iz primjera 1.1 se vidi da je
Pretpostavimo da postoji inverz
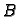
matrice
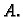
Tada je
tj.
što je u kontradikciji s definicijom jednakosti
matrica.
Može se dokazati da vrijedi
za svaki 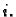 No, ako algebarske komplemente
elemenata jednog retka množimo s elementima drugog retka i zbrojimo,
dobivamo nulu
No, ako algebarske komplemente
elemenata jednog retka množimo s elementima drugog retka i zbrojimo,
dobivamo nulu
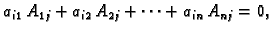
za
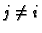
To slijedi odatle što je lijeva
strana jednaka determinanti u kojoj je umjesto 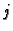 -tog retka napisan
-tog retka napisan
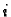 -ti. Tako u determinanti imamo dva retka jednaka, pa je ona jednaka
nuli. Dakle za svaki
-ti. Tako u determinanti imamo dva retka jednaka, pa je ona jednaka
nuli. Dakle za svaki 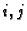 vrijedi
Na lijevoj strani ove jednakosti se nalazi
vrijedi
Na lijevoj strani ove jednakosti se nalazi 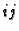 -ti element
produkta matrice
-ti element
produkta matrice
![$ A=[a_{ij}]$](img62.gif) i matrice
i matrice
![$ B=[A_{ij}].$](img193.gif) Vidimo da je
tj.
Odgovarajuće formule vrijede ako se uzmu stupci matrice
Vidimo da je
tj.
Odgovarajuće formule vrijede ako se uzmu stupci matrice  umjesto redaka, pa se može slično dobiti formula
Odavde je jasno da je
Matrica
umjesto redaka, pa se može slično dobiti formula
Odavde je jasno da je
Matrica
![$ B = [A_{ij}]$](img198.gif) se zove adjunkta matrice
se zove adjunkta matrice
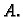
Na temelju ove diskusije može se zaključiti da vrijedi i obrat 6. svojstva skupa regularnih matrica 1.1.2. Tako vrijedi
6'. Matrica  je regularna ako i samo ako je
je regularna ako i samo ako je
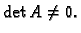
Definicija 8

-torku realnih brojeva
zovemo
vektorstupcem, a
vektorretkom. Uglavnom
ćemo raditi s vektorstupcima, pa ćemo njih jednostavno zvati
vektorima. Kraće ćemo ih
zapisivati
Skup svih vektorstupaca ćemo označavati s
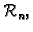 a svih
vektorredaka s
a svih
vektorredaka s
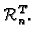
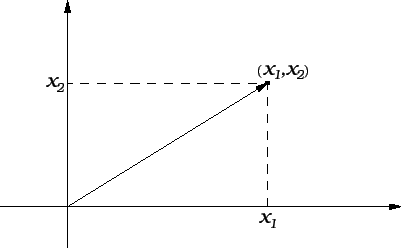
Kako je vektor
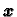 u
u
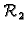 zadan s dva realna broja, od
kojih se zna koji je prvi, a koji drugi, možemo
zadan s dva realna broja, od
kojih se zna koji je prvi, a koji drugi, možemo
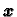 identificirati s uređenim parom realnih brojeva, dakle točkom u
ravnini, a prema tome i s radijvektorom u ravnini.
identificirati s uređenim parom realnih brojeva, dakle točkom u
ravnini, a prema tome i s radijvektorom u ravnini.
Slika 1.1:
Vektorstupac u
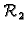 kao vektor u ravnini
kao vektor u ravnini
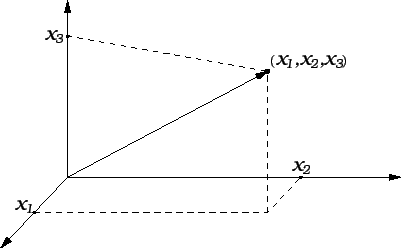
Vektor
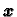 u
u
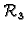 je zadan s tri realna broja, od
kojih se zna koji je prvi, koji je drugi, a koji je treći. Tako
možemo
je zadan s tri realna broja, od
kojih se zna koji je prvi, koji je drugi, a koji je treći. Tako
možemo
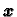 identificirati s uređenom trojkom realnih
brojeva, dakle točkom u prostoru, a prema tome i s radijvektorom u
prostoru.
identificirati s uređenom trojkom realnih
brojeva, dakle točkom u prostoru, a prema tome i s radijvektorom u
prostoru.
Slika 1.2:
Vektorstupac u
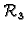 kao vektor u prostoru
kao vektor u prostoru
Kao što smo vidjeli
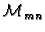 je vektorski prostor. Tako su i
je vektorski prostor. Tako su i
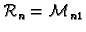 i
i
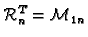 vektorski
prostori.
vektorski
prostori.
Budući da su vektori ustvari jednostupčaste matrice, znamo ih
zbrajati i množiti brojem. Također znamo što je vektor 0 i
taj vektor zovemo nulvektorom.
Operacije, koje su dane u
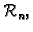 omogućavaju da pravimo linearne
kombinacije vektora. Neka su dani vektori
omogućavaju da pravimo linearne
kombinacije vektora. Neka su dani vektori
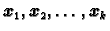 istog tipa, i brojevi
istog tipa, i brojevi
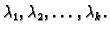 Linearnom kombinacijom vektora
Linearnom kombinacijom vektora
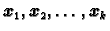 zovemo vektor
zovemo vektor
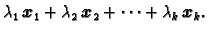 |
(1.3) |
Brojeve
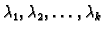 zovemo
koeficijentima linearne kombinacije
(1.3).
zovemo
koeficijentima linearne kombinacije
(1.3).
Definicija 9
Za vektore
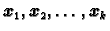
kažemo da su
linearno nezavisni, ako
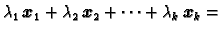 0
0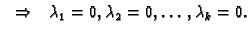
U protivnom kažemo da
su
linearno zavisni.
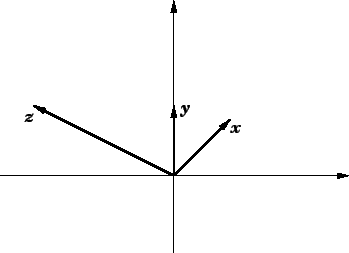
Primjer 1.4
Neka su dana tri vektora
Tada je
Kako su koeficijenti u linearnoj kombinaciji različiti od
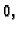
ti
vektori su linearno zavisni.
Na slici 1.3 su vektori u ravnini reprezentirani
radijvektorima, i pokazano je kako linearna kombinacija iščezava.
Slika 1.3:
Linearna zavisnost vektora
Pokušajte se uvjeriti crtežom da linearna kombinacija dva od njih,
na pr.
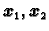 daje
daje
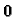 samo
u slučaju da su koeficijenti linearne kombinacije jednaki
samo
u slučaju da su koeficijenti linearne kombinacije jednaki 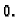
Primjer 1.5
Ispitati linearnu nezavisnost sljedećih vektora u odnosu na parametre
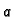
i
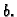
Rješenje. Jednakost
vodi na sustav jednadžbi
Slijedi
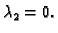
Ostaju tri jednadžbe s tri
nepoznanice. Eliminiramo nepoznanicu
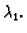
Ostaju dvije
jednadžbe s nepoznanicama
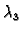
i
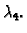
Odatle dobivamo jednu jednadžbu
Ako je
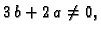
onda je
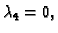
i zatim
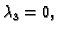
i kad se s tim vratimo u početni sustav dobivamo i
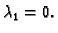
Dakle, za
vektori su linearno nezavisni.
U protivnom, ako je
onda
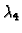
može biti proizvoljan broj, prema tome i različit
od
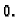
Tako su, u tom slučaju, vektori linearno zavisni.
Skalarni produkt.
U
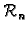 možemo definirati skalarni produkt na sljedeći
način.
možemo definirati skalarni produkt na sljedeći
način.
Definicija 10
Neka su
![$ \boldsymbol{x}=\left[x_{i}\right]$](img244.gif)
i
![$ \boldsymbol{y}=\left[y_{i}\right]$](img245.gif)
proizvoljni vektori u
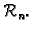 Skalarni
produkt
Skalarni
produkt vektora
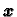
i
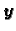
je broj (skalar)
Vektore možemo shvatiti kao jednostupčaste matrice. U tom slučaju
se skalarni produkt može zapisati kao
Skalarni produkt ima sljedeća svojstva.
- 1.
-
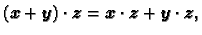
- 2.
-
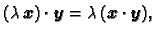
- 3.
-
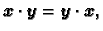
- 4.
-
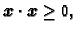
- 5.
-
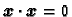 ako i samo ako je
ako i samo ako je
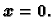
U vektorskom prostoru radijvektora (usmjerenih dužina) smo pomoću
skalarnog produkta računali duljine vektora, kuteve između njih, i
prema tome rješavali određene geometrijske probleme. Koristeći
skalarni produkt to možemo sada i u
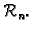 Tako kažemo da je
duljina
vektora
Tako kažemo da je
duljina
vektora
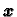
a kut 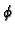 između
vektora
između
vektora
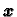 i
i
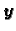 se računa iz formule
se računa iz formule
Pomoću skalarnog produkta vektora možemo kraće zapisati umnožak
dvije matrice. Označimo s
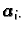
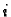 -ti redak matrice
-ti redak matrice
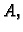 a s
a s
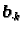
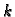 -ti stupac matrice
-ti stupac matrice 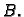 Iz uvjeta za
postojanje produkta matrica slijedi da ti vektori imaju jednak broj
elemenata, tj. oni pripadaju istom vektorskom prostoru, pa se mogu
skalarno množiti. Prema definiciji umnoška matrica možemo pisati
Iz uvjeta za
postojanje produkta matrica slijedi da ti vektori imaju jednak broj
elemenata, tj. oni pripadaju istom vektorskom prostoru, pa se mogu
skalarno množiti. Prema definiciji umnoška matrica možemo pisati
Produkt matrice i vektora.
Neka je
![$ A=[a_{ij}]$](img62.gif) matrica tipa
matrica tipa 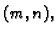 i
i
![$ \boldsymbol{x}=[x_j]\in {\cal R}_{n}$](img263.gif) proizvoljan vektor. Vektor možemo shvatiti kao jednostupčastu
matricu, te možemo pomnožiti
proizvoljan vektor. Vektor možemo shvatiti kao jednostupčastu
matricu, te možemo pomnožiti  i
i
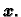 Dobivamo
Dobivamo
ili raspisano
Dakle
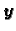 je vektor u
je vektor u
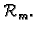 Tako množenje matricom
Tako množenje matricom  tipa
tipa
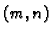 možemo shvatiti kao funkciju koja preslikava vektore iz
možemo shvatiti kao funkciju koja preslikava vektore iz
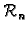 u
vektore iz
u
vektore iz
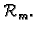
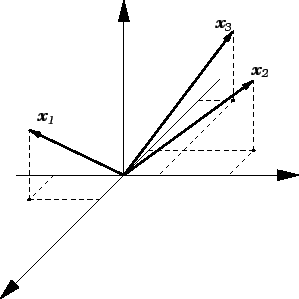
Primjer 1.6
Na pr. matrica
djeluje kao preslikavanje iz
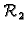
u
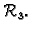
Na slici
1.4 su prikazani vektorstupci
kad radijvektori. Slika
1.5 predstavlja njihove slike
nakon djelovanja matrice (nakon množenja s matricom).
Slika 1.4:
Vektori u
Slika 1.5:
Slike vektora iz
To preslikavanje je linearno,
jer vrijedi
za bilo koje brojeve
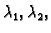 i bilo koje vektore
i bilo koje vektore
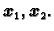
Definicija 11
Neka su
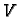
i
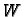
dva vektorska prostora, i neka je

funkcija sa svojstvom
za svaki par vektora
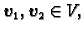
i
za svaki par brojeva
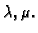
Takvu funkciju zovemo
linearnim
operatorom.
U skladu s ovom definicijom, matricu  tipa
tipa 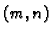 možemo smatrati
linearnim operatorom s prostora
možemo smatrati
linearnim operatorom s prostora
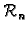 u prostor
u prostor
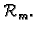
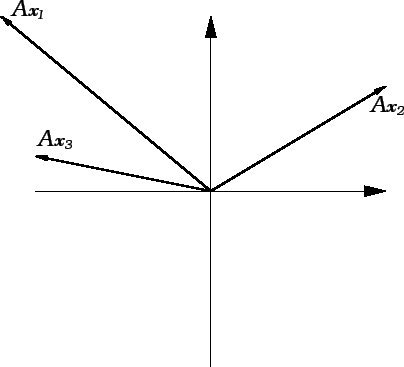
Slike 1.6 i 1.7 pokazuju kako djeluje matrica
kao preslikavanje iz
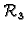 u
u
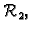 kad vektorstupce
identificiramo s radijvektorima.
kad vektorstupce
identificiramo s radijvektorima.
Slika 1.6:
Vektori u
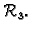
Slika 1.7:
Slike vektora iz
Baza
Definicija 12
Neka je
vektorski prostor.
Bazom u
vektorskom prostoru
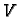
zovemo uređenu
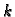
-torku vektora
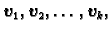
ako su ti vektori
- 1.
- linearno nezavisni,
- 2.
- razapinju vektorski prostor
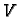 , tj. ako se svaki vektor iz
, tj. ako se svaki vektor iz 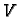 može napisati kao linearna kombinacija vektora
može napisati kao linearna kombinacija vektora
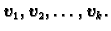
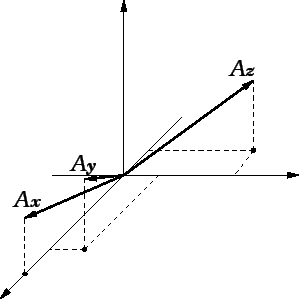
Vidjeli smo da se vektorstupci u
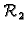 i
i
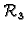 mogu identificirati
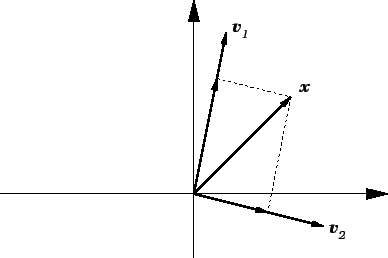
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kao
se vektor
mogu identificirati
s radijvektorima, i prema tome crtati u ravnini i prostoru. U ravnini,
preciznije u vektorskom prostoru radijvektora u ravnini, bilo koja dva
nekolinearna vektora čine bazu. Na slici 1.8 se vidi kao
se vektor
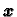 može prikazati kao linearna kombinacija dva
nekolinearna vektora
može prikazati kao linearna kombinacija dva
nekolinearna vektora
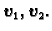
Slika 1.8:
Baza u
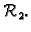
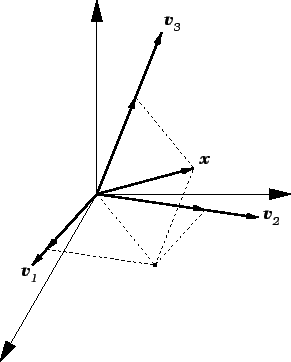
Također, u vektorskom prostoru radijvektora u prostoru bilo koja tri
nekomplanarna vektora čine bazu. Na slici 1.9 se vidi kao
se vektor
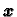 može prikazati kao linearna kombinacija tri
nekomplanarna vektora
može prikazati kao linearna kombinacija tri
nekomplanarna vektora
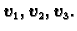
Slika 1.9:
Baza u
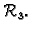
Primjer 1.7
Neka su zadani vektori u
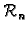
Ovi vektori čine bazu u
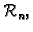
i ta baza se
zove
kanonska baza u
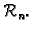
Rješenje. Zaista,
i također
povlači
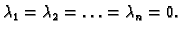
Prema tome ovi
vektori razapinju
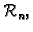
i linearno su nezavisni.
Primjer 1.8
Neka su zadane matrice u
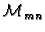
One čine bazu u
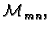
i ta baza se
zove
kanonska baza u
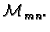
Rješenje. Zaista,
i također
povlači
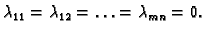
Prema tome ovi
vektori razapinju
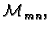
i linearno su nezavisni.
Teorem 2
Svaki vektor se na jedinstven način prikazuje kao linearna
kombinacija vektora baze.
Dokaz. Neka je 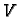 vektorski
prostor, neka je
vektorski
prostor, neka je
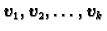 baza u
baza u 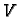 i neka je
i neka je
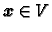 proizvoljan. Zbog drugog svojstva baze
imamo
proizvoljan. Zbog drugog svojstva baze
imamo
Pretpostavimo da je također
Tada je
Zbog linearne nezavisnosti
baze, slijedi
Dakle, nije moguće da
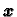 ima dva
različita prikaza u
ima dva
različita prikaza u 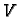 u odnosu na izabranu bazu.
u odnosu na izabranu bazu.
Teorem 3
[
1, str. 141]
Neka je u vektorskom prostoru
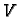
dano
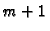
međusobno različitih
vektora
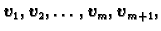
i neka se
svaki od njih može napisati kao linearna kombinacija od
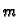
vektora
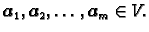
Tada su vektori
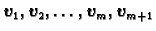
linearno zavisni.
Dokaz. Teorem ćemo dokazati
matematičkom indukcijom. Za 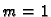 tvrdnja vrijedi, jer iz
tvrdnja vrijedi, jer iz
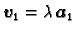 i
i
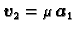 slijedi
slijedi
odakle
pa su vektori
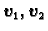 linearno zavisni. Ako je
linearno zavisni. Ako je
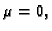 onda se ne može dijeliti s
onda se ne može dijeliti s 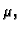 no u tom slučaju je
no u tom slučaju je
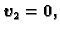 pa su vektori
pa su vektori
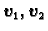 linearno zavisni, jer vrijedi
Pretpostavimo da tvrdnja vrijedi za svaki prirodni broj
linearno zavisni, jer vrijedi
Pretpostavimo da tvrdnja vrijedi za svaki prirodni broj 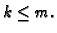 Dokažimo da tvrdnja vrijedi i za
Dokažimo da tvrdnja vrijedi i za 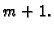 Po pretpostavci imamo
Kad bi svaki koeficijent uz
Po pretpostavci imamo
Kad bi svaki koeficijent uz
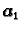 bio jednak
nuli, onda bismo imali situaciju da su vektori
bio jednak
nuli, onda bismo imali situaciju da su vektori
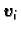 linearne kombinacije od
linearne kombinacije od 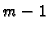 vektora, pa bi po pretpostavci indukcije
bili linearno zavisni. Stoga možemo pretpostaviti da je na primjer
vektora, pa bi po pretpostavci indukcije
bili linearno zavisni. Stoga možemo pretpostaviti da je na primjer
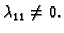 Pomnožimo prvu jednadžbu s
Pomnožimo prvu jednadžbu s
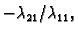 i dodajmo je drugoj. Time vektor
i dodajmo je drugoj. Time vektor
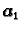 iščezne iz druge jednadžbe. Zatim, pomnožimo
prvu jednadžbu s
iščezne iz druge jednadžbe. Zatim, pomnožimo
prvu jednadžbu s
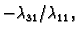 i dodajmo je
trećoj. Time vektor
i dodajmo je
trećoj. Time vektor
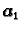 iščezne iz treće
jednadžbe, itd. Nakon tog postupka druga, treća i ostale jednadžbe
izgledaju ovako
Po pretpostavci indukcije slijedi da su vektori
iščezne iz treće
jednadžbe, itd. Nakon tog postupka druga, treća i ostale jednadžbe
izgledaju ovako
Po pretpostavci indukcije slijedi da su vektori
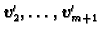 linearno zavisni. Pri
tom je
To
znači da postoje brojevi
linearno zavisni. Pri
tom je
To
znači da postoje brojevi
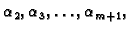 od kojih je barem
jedan različit od nule, takvi da je
odnosno vrijedi
za barem jedan
od kojih je barem
jedan različit od nule, takvi da je
odnosno vrijedi
za barem jedan
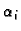 različit od nule, pa su prema
tome vektori
različit od nule, pa su prema
tome vektori
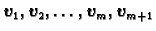 linearno zavisni. Kako su time ispunjene pretpostavke aksioma
matematičke indukcije, tvrdnja vrijedi za svaki prirodni broj
linearno zavisni. Kako su time ispunjene pretpostavke aksioma
matematičke indukcije, tvrdnja vrijedi za svaki prirodni broj 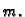
Posljedice.
- 1.
- Svaka četiri vektora u
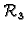 su linearno zavisna.
su linearno zavisna.
- 2.
- Ako su vektori
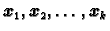 iz
iz
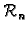 linearno
nezavisni, onda je
linearno
nezavisni, onda je 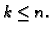
- 3.
- Ako je svaki vektor iz
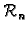 linearna kombinacija vektora
linearna kombinacija vektora
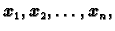 onda su vektori
onda su vektori
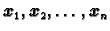 linearno
nezavisni, i prema tome čine bazu.
linearno
nezavisni, i prema tome čine bazu.
- 4.
- Svaka baza u vektorskom prostoru
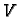 ima jednaki broj elemenata.
(Broj vektora u bazi se zove dimenzija prostora
ima jednaki broj elemenata.
(Broj vektora u bazi se zove dimenzija prostora 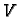 i
označava s
i
označava s 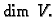 )
)
- 5.
-
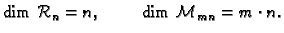

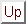



Next: Sustavi linearnih algebarskih jednadžbi
Up: Matrice i sustavi jednadžbi
Previous: Matrice i sustavi jednadžbi
Contents
Index
Salih Suljagic
1999-12-17
![\begin{displaymath}
% latex2html id marker 29810
A=\left[
\begin{array}{cccc}
a...
...dots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{array}\right]\end{displaymath}](img41.gif)
![]() onda kažemo da je
onda kažemo da je ![]() kvadratna
matrica reda
kvadratna
matrica reda ![]() .
.
![]() čine i-ti redak
čine i-ti redak
![]() čine j-ti stupac; dakle
čine j-ti stupac; dakle
![]() je element matrice, koji se nalazi u
je element matrice, koji se nalazi u ![]() -tom retku i
-tom retku i ![]() -tom
stupcu.
-tom
stupcu.
![]() označavamo skup svih matrica tipa
označavamo skup svih matrica tipa ![]() Ako je
Ako je
![]() onda se piše
onda se piše
![]() umjesto
umjesto
![]()
![$\displaystyle A\,B=\left[c_{ik}\right]= \left[\sum_{j=1}^{n}
a_{ij}\,b_{jk}\right].$](img89.gif)
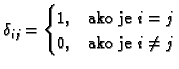
![\begin{displaymath}
% latex2html id marker 29997
A=[a_{ij}]=\left[
\begin{array}...
...ots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{array}\right].\end{displaymath}](img108.gif)
![\begin{displaymath}
% latex2html id marker 30007
A^T=[a^T_{ij}]=[a_{ji}]=\left[
...
...ts \\
a_{1n} & a_{2n} & \cdots & a_{mn}
\end{array}\right].
\end{displaymath}](img112.gif)
![% latex2html id marker 30054
$\displaystyle A=\left[\begin{array}{cc}
1 & 0 \\ ...
...ght],\hspace{1cm}B=\left[\begin{array}{cc}
a & b \\
c & d
\end{array}\right].$](img127.gif)
![% latex2html id marker 30056
$\displaystyle A\,B=\left[\begin{array}{cc}
a & b \...
...],\hspace{1cm}B\,A=\left[\begin{array}{cc}
a & 0 \\
c & 0
\end{array}\right],$](img128.gif)
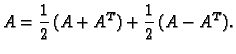
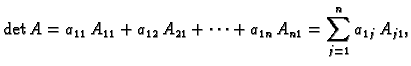

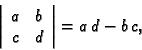
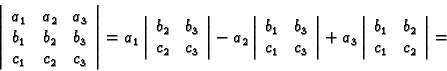
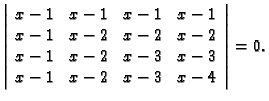


![% latex2html id marker 30247
$\displaystyle A=\left[\begin{array}{cc}
1 & 0 \\
0 & 0
\end{array}\right]$](img183.gif)
![% latex2html id marker 30249
$\displaystyle A\,\left[\begin{array}{cc}
0 & 0 \\ ...
...\end{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right].$](img184.gif)
![% latex2html id marker 30255
$\displaystyle BA\,\left[\begin{array}{cc}
0 & 0 \\...
...d{array}\right]=B\,\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right],$](img185.gif)
![% latex2html id marker 30257
$\displaystyle \left[\begin{array}{cc}
0 & 0 \\
0...
...\end{array}\right]=\left[\begin{array}{cc}
0 & 0 \\
0 & 0
\end{array}\right],$](img186.gif)
![$\displaystyle A^{-1} = \frac{1}{\det
A}\,[A_{ij}].$](img197.gif)
![% latex2html id marker 30302
$\displaystyle \boldsymbol{x}=\left[ \begin{array}{c}
x_{1} \\ x_{2} \\ \vdots \\ x_{n}
\end{array} \right]$](img199.gif)
![% latex2html id marker 30365
$\displaystyle \boldsymbol{x}_1=\left[
\begin{array...
...t],\quad \boldsymbol{x}_3=\left[
\begin{array}{r}
-1 \\ -2
\end{array}\right].$](img213.gif)
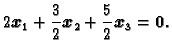
![% latex2html id marker 30386
$\displaystyle \boldsymbol{x}_1 = \left[\begin{arra...
...ldsymbol{x}_4 = \left[\begin{array}{c} a \\
1 \\ 0 \\ 5 \end{array}\right].$](img221.gif)
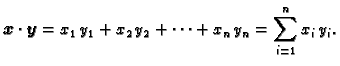
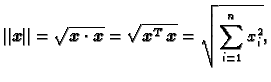
![% latex2html id marker 30560
$\displaystyle \left[\begin{array}[center]{cc}
2 & 3 \\ -1 & 1 \\ 0 & 2
\end{array}\right]$](img274.gif)
![% latex2html id marker 30566
$\displaystyle \boldsymbol{x}= \left[ \begin{array}...
...ght],\quad
\boldsymbol{z}= \left[ \begin{array}{c}
-2 \\ 1
\end{array}\right]$](img275.gif)
![% latex2html id marker 30611
$\displaystyle \left[\begin{array}[center]{ccc}
2 & 3 & -1 \\ 1 & 0 & 2
\end{array}\right]$](img287.gif)
![% latex2html id marker 30617
$\displaystyle \boldsymbol{x}_1 = \left[\begin{arra...
...dsymbol{x}_3 = \left[\begin{array}[center]{c}
-3 \\ 1 \\ 2
\end{array}\right]$](img289.gif)
![% latex2html id marker 30684
$\displaystyle \boldsymbol{e}_1=\left[\begin{array}...
...ymbol{e}_n=\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 1
\end{array} \right].$](img298.gif)
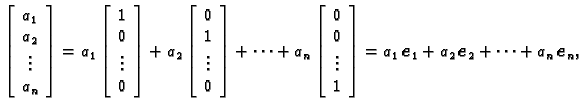
![% latex2html id marker 30692
$\displaystyle \lambda_1\left[\begin{array}{c}
1 \...
...y} \right]=\left[\begin{array}{c}
0 \\ 0 \\ \vdots \\ 0
\end{array} \right]$](img300.gif)
![% latex2html id marker 30701
$\displaystyle E_{11}=\left[\begin{array}{cccc}
1 &...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{array} \right].$](img302.gif)
![% latex2html id marker 30707
$\displaystyle \left[\begin{array}{cccc}
a_{11} & a...
...\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0
\end{array} \right] +$](img304.gif)
![% latex2html id marker 30709
$\displaystyle \cdots+a_{mn}\left[\begin{array}{ccc...
...ts & 1
\end{array} \right]=a_{11}\,E_{11}+a_{12}\,E_{12}+\cdots+a_{mn}\,E_{mn},$](img305.gif)
![% latex2html id marker 30711
$\displaystyle \lambda_{11}\left[\begin{array}{cccc...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{array} \right]$](img306.gif)
![% latex2html id marker 30713
$\displaystyle =\left[\begin{array}{cccc}
\lambda_{...
...
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 0
\end{array} \right]$](img307.gif)