



Next: Problem vlastitih ...
Up: Matrice i sustavi jednadžbi
Previous: Vektori i matrice
Contents
Index
Subsections
Sustav linearnih algebarskih jednadžbi
Za 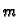 jednadžbi s
jednadžbi s  nepoznanica oblika
nepoznanica oblika
kažemo da čine sustav linearnih algebarskih jednadžbi.
Brojeve
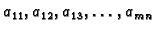 zovemo koeficijentima sustava,
zovemo koeficijentima sustava,
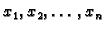 se zovu nepoznanice, a brojeve
se zovu nepoznanice, a brojeve
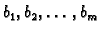 zovemo desnom
stranom ili slobodnim članovima.
Koeficijenti i slobodni članovi su zadani, a nepoznanice treba
odrediti. Ako je
zovemo desnom
stranom ili slobodnim članovima.
Koeficijenti i slobodni članovi su zadani, a nepoznanice treba
odrediti. Ako je 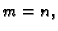 onda sustav zovemo kvadratnim. Ako je
desna strana sastavljena od samih nula, onda sustav zovemo
homogenim, u protivnom,
ako je
onda sustav zovemo kvadratnim. Ako je
desna strana sastavljena od samih nula, onda sustav zovemo
homogenim, u protivnom,
ako je 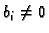 za bar jedan
za bar jedan 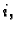 zovemo ga nehomogenim.
zovemo ga nehomogenim.
U vezi sa sustavom možemo uočiti dvije matrice
Matricu  zovemo matricom sustava, a matricu
zovemo matricom sustava, a matricu 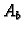 zovemo
proširenom matricom
sustava.
zovemo
proširenom matricom
sustava.
Pojam rješenja
Rješenje sustava
1.4 je uređena  -torka brojeva
-torka brojeva
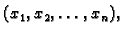 koja zadovoljava svaku od jednadžbi u
sustavu. Sustav može imati jedno rješenje, više rješenja i niti
jedno rješenje. Ako ne postoji rješenje onda kažemo da je sustav
nekonzistentan ili
nemoguć ili
protuslovan.
koja zadovoljava svaku od jednadžbi u
sustavu. Sustav može imati jedno rješenje, više rješenja i niti
jedno rješenje. Ako ne postoji rješenje onda kažemo da je sustav
nekonzistentan ili
nemoguć ili
protuslovan.
Ako je sustav homogen, onda je očito  -torka
-torka
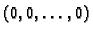 rješenje. To rješenje se zove trivijalno. Pravi
problem kod homogenih sustava je da li postoje rješenja različita od
trivijalnog, tj. da li postoje netrivijalna rješenja.
rješenje. To rješenje se zove trivijalno. Pravi
problem kod homogenih sustava je da li postoje rješenja različita od
trivijalnog, tj. da li postoje netrivijalna rješenja.
Ekvivalentni sustavi
Za dva sustava, koji ne moraju imati isti broj jednadžbi, kažemo da
su ekvivalentni,
ako je skup svih rješenja jednog od njih jednak skupu svih rješenja
drugog. U želji da riješimo zadani sustav vršimo nad njim određene
operacije kako bismo ga pojednostavili. Operacije, koje smijemo
vršiti su one koje vode na ekvivalentni sustav. To su
- 1.
- zamjena redosljeda jednadžbi u sustavu,
- 2.
- množenje proizvoljne jednadžbe sustava brojem različitim
od nule,
- 3.
- množenje proizvoljne jednadžbe sustava brojem, i dodavanje
rezultata bilo kojoj drugoj jednadžbi sustava.
Gaussov postupak eliminacije
Gaussov postupak eliminacije je metoda rješavanja sustava
linearnih algebarskih jednadžbi. Ideja je sljedeća. Operacijama,
koje smo gore naveli, zadani sustav svesti na njemu ekvivalentan,
tako da iz dobivenog sustava lako nađemo skup svih rješenja.
Neka je zadan sustav 1.4. Premjestimo jednadžbe u
sustavu, ako je potrebno, tako da koeficijent uz 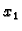 u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz
u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz 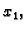 pomnožimo brojem koji je suprotan
koeficijentu uz
pomnožimo brojem koji je suprotan
koeficijentu uz 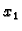 u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz
u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz 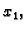 pomnožimo brojem koji je suprotan koeficijentu uz
pomnožimo brojem koji je suprotan koeficijentu uz 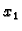 u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz
u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz 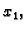 pomnožimo brojem koji je
suprotan koeficijentu uz
pomnožimo brojem koji je
suprotan koeficijentu uz 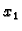 u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili
u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili 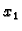 iz
druge, treće,
iz
druge, treće, 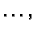
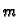 -te jednadžbe i došli do ekvivalentnog
sustava oblika
-te jednadžbe i došli do ekvivalentnog
sustava oblika
pri tom je
odnosno općenito
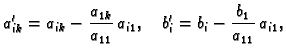
za
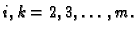
Sad učinimo isto s podsustavom, koji se
sastoji od druge, treće, ..., 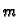 -te jednadžbe. Time iz treće i
daljnjih jednadžbi eliminiramo
-te jednadžbe. Time iz treće i
daljnjih jednadžbi eliminiramo 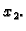 Zatim na isti način iz
četvrte i daljnjih jednadžbi izbacimo
Zatim na isti način iz
četvrte i daljnjih jednadžbi izbacimo 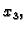 i t.d. Budući da
sustav ima konačno mnogo jednadžbi, postupak staje nakon konačno
koraka. Dobije se ekvivalentan sustav, po obliku ``trokutast''. Sada
najprije riješimo zadnju jednadžbu, rješenje uvrstimo u predzadnju,
pa nju riješimo, pa uvrstimo u treću straga i t.d. sve do prve
jednadžbe. Metoda, koju smo opisali, zove se Gaussova metoda eliminacije.
i t.d. Budući da
sustav ima konačno mnogo jednadžbi, postupak staje nakon konačno
koraka. Dobije se ekvivalentan sustav, po obliku ``trokutast''. Sada
najprije riješimo zadnju jednadžbu, rješenje uvrstimo u predzadnju,
pa nju riješimo, pa uvrstimo u treću straga i t.d. sve do prve
jednadžbe. Metoda, koju smo opisali, zove se Gaussova metoda eliminacije.
Dakle ideja Gaussove metode eliminacije se sastoji u tome da se
pomoću operacija 1.2.1 izbace nepoznanice koje se nalaze
ispod ``glavne dijagonale''.
Primjer 1.9
Treba riješiti sustav
Množenjem prve jednadžbe s
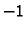
i dodavanjem trećoj, i zatim
množenjem prve jednadžbe s
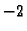
i dodavanjem četvrtoj, dobivamo
Zamijenimo mjesta treće i druge jednadžbe, i zatim drugu
množimo s
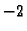
i s
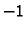
i dodamo redom trećoj i četvrtoj jednadžbi.
Pomnožimo treću jednadžbu s
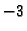
i dodajmo četvrtoj
Dobili smo ``trokutast'' oblik, i sada rješavamo jednadžbe
odozdo prema gore. Iz zadnje slijedi
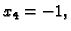
uvrstimo to u
treću, pa slijedi
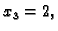
uvrstimo u drugu, pa slijedi
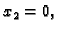
uvrstimo u prvu, pa slijedi
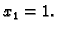
Metodu eliminacije možemo upotrebiti i nakon svođenja na
``trokutasti'' oblik da bismo izbacili nepoznanice iznad ``glavne
dijagonale'' i došli tako do ``dijagonalnog'' oblika. Ta metoda se
zove Gauss-Jordanova metoda. Na sljedećem
primjeru pokažimo kako funkcionira ta metoda.
Primjer 1.10
Treba riješiti sustav
Kao u gornjem primjeru nakon nekoliko koraka dolazimo do
Množimo četvrtu jednadžbu redom s
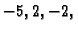
i dodajemo redom
trećoj, drugoj, prvoj jednadžbi. Dobivamo
Dodajmo još treću prvoj. Tako dolazimo do ``dijagonalnog''
oblika
Odatle čitamo rješenje
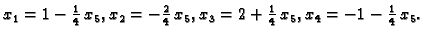
U ovom primjeru se pojavljuje 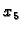 kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za
kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za 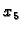 pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja.
pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja. 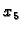 može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.
može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.
Neka je dan štap (greda, ploča, štapna konstrukcija). Pod
djelovanjem sila štap doživi progib. Interesira nas iz zadanog
progiba naći sile koje koje su uzrokovale taj progib.
Odredimo  točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih
točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih  točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
- 1.
- Pri istovremenom djelovanju dviju sila progibi se zbrajaju.
- 2.
- Koliko puta povećamo silu, toliko puta se poveća progib.
Označimo s 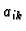 progib u čvoru
progib u čvoru 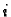 uslijed djelovanja jedinične
sile u čvoru
uslijed djelovanja jedinične
sile u čvoru 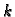 (sl. 1.10).
(sl. 1.10).
Slika 1.10:
Pomak štapa pod djelovanjem jedinične sile u čvoru 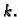
Označimo s
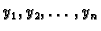 ukupne progibe, a s
ukupne progibe, a s
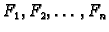 sile u čvorovima (sl. 1.11).
sile u čvorovima (sl. 1.11).
Slika 1.11:
Pomak štapa pod djelovanjem različitih sila u čvorovima.
Tada vrijede sljedeće jednadžbe
Vidimo da problem nalaženja sila iz zadanih progiba vodi na
rješavanje sustava linearnih algebarskih jednadžbi.
Pretpostavimo sada da u čvoru 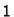 djeluje sila
djeluje sila 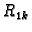 takva da
poništava utjecaj jedinične sile u čvoru
takva da
poništava utjecaj jedinične sile u čvoru 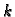 na čvor
na čvor 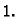
Slika 1.12:
Pomak štapa pod djelovanjem jedinične sile u čvoru 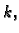 nakon uravnoteženja u čvoru
nakon uravnoteženja u čvoru 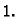
U ovoj situaciji označimo s
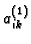 progib u čvoru
progib u čvoru 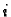 uslijed djelovanja jedinične sile u čvoru
uslijed djelovanja jedinične sile u čvoru 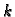 (sl. 1.12). Tada vrijedi
za
(sl. 1.12). Tada vrijedi
za
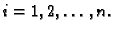 Specijalno u čvoru
Specijalno u čvoru 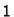 imamo
Odatle slijedi
pa je
za
imamo
Odatle slijedi
pa je
za
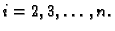 Ako tako učinimo za svaki
Ako tako učinimo za svaki
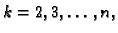 dobijemo koeficijente nakon prvog koraka u Gaussovoj metodi. Slično
bi se moglo pokazati da se koeficijenti nakon drugog koraka dobiju kad
u prva dva čvora djeluju sile koje poništavaju progibe uslijed
djelovanja jedinične sile u ostalim čvorovima, itd. Detaljnije o
tome u [6].
dobijemo koeficijente nakon prvog koraka u Gaussovoj metodi. Slično
bi se moglo pokazati da se koeficijenti nakon drugog koraka dobiju kad
u prva dva čvora djeluju sile koje poništavaju progibe uslijed
djelovanja jedinične sile u ostalim čvorovima, itd. Detaljnije o
tome u [6].
Elementarne transformacije
Elementarnim
transformacijama nad matricom zovemo sljedeće operacije:
- 1.
- zamjena dva retka (dva stupca) u matrici,
- 2.
- množenje proizvoljnog retka (stupca) brojem
različitim od nule,
- 3.
- množenje proizvoljnog retka (stupca) matrice brojem, i dodavanje
bilo kojem drugom retku (stupcu) matrice.
Ako je matrica 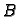 dobivena iz matrice
dobivena iz matrice  primjenom jedne ili više
elementarnih operacija, onda pišemo
primjenom jedne ili više
elementarnih operacija, onda pišemo
i kažemo da je matrica 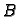 ekvivalentna
matrici
ekvivalentna
matrici 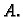
Kako pokazuju sljedeći primjeri, ove operacije se mogu ostvariti
množenjem matrice regularnim matricama s lijeva ili s desna.
Primjer 1.11
Dakle, množeći matricu s lijeva jediničnom matricom u kojoj su
zamijenjeni drugi i treći redak, dobili smo matricu u kojoj su
zamijenjeni drugi i treći redak.
Množeći matricu s desna jediničnom matricom u kojoj su
zamijenjeni drugi i treći stupac, dobili smo matricu u kojoj su
zamijenjeni drugi i treći stupac.
Primjer 1.12
Dakle, množeći matricu s lijeva jediničnom matricom u kojoj je
treći redak pomnožen brojem 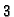 (različitim od nule), dobili smo
matricu u kojoj je treći redak pomnožen brojem
(različitim od nule), dobili smo
matricu u kojoj je treći redak pomnožen brojem 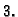
Množeći matricu s desna jediničnom matricom u kojoj je
drugi stupac pomnožen brojem 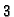 (različitim od nule), dobili smo
matricu u kojoj je drugi stupac pomnožen brojem
(različitim od nule), dobili smo
matricu u kojoj je drugi stupac pomnožen brojem 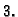
Primjer 1.13
Dakle, množeći matricu s lijeva jediničnom matricom u kojoj smo
prvi redak pomnožili brojem 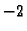 i dodali četvrtom, dobili smo
matricu u kojoj je prvi redak pomnožen brojem
i dodali četvrtom, dobili smo
matricu u kojoj je prvi redak pomnožen brojem 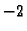 dodan
četvrtom retku.
dodan
četvrtom retku.
Množeći matricu s desna jediničnom matricom u kojoj smo treći
stupac pomnožili brojem 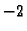 i dodali prvom, dobili smo matricu u
kojoj je treći stupac pomnožen brojem
i dodali prvom, dobili smo matricu u
kojoj je treći stupac pomnožen brojem 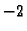 dodan prvom stupcu.
dodan prvom stupcu.
Zaključak.
- 1.
- Što želimo učiniti s recima matrice
 učinimo to s recima
jedinične matrice i s tako dobivenom matricom množimo matricu
učinimo to s recima
jedinične matrice i s tako dobivenom matricom množimo matricu  s lijeva.
s lijeva.
- 2.
- Što želimo učiniti sa stupcima matrice
 učinimo to sa
stupcima jedinične matrice i s tako dobivenom matricom množimo
matricu
učinimo to sa
stupcima jedinične matrice i s tako dobivenom matricom množimo
matricu  s desna.
s desna.
Ove intervencije na jediničnoj matrici dovode do regularnih
matrica. Zaista, ako jediničnu matricu u kojoj su zamijenjeni drugi i
treći redak (stupac) pomnožimo s istom takvom s lijeva (s desna),
dobit ćemo jediničnu matricu. Ako jediničnu matricu u kojoj je
treći redak (stupac) pomnožen brojem 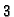 pomnožimo s lijeva (s
desna) s jediničnom matricom u kojoj je treći redak (stupac)
pomnožen brojem
pomnožimo s lijeva (s
desna) s jediničnom matricom u kojoj je treći redak (stupac)
pomnožen brojem
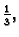 dobit ćemo jediničnu matricu. Ako
jediničnu matricu u kojoj je trećem retku (stupcu) dodan prvi
pomnožen s
dobit ćemo jediničnu matricu. Ako
jediničnu matricu u kojoj je trećem retku (stupcu) dodan prvi
pomnožen s 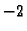 pomnožimo s lijeva (s desna) s jediničnom matricom
u kojoj je trećem retku (stupcu) dodan prvi pomnožen s
pomnožimo s lijeva (s desna) s jediničnom matricom
u kojoj je trećem retku (stupcu) dodan prvi pomnožen s 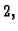 dobit
ćemo jediničnu matricu.
dobit
ćemo jediničnu matricu.
Ove matrice koje vrše elementarne operacije zvat ćemo
elementarnim matricama.
Gaussov i Gauss-Jordanov postupak eliminacije se može provoditi tako
da se nad proširenom matricom sustava provode elementarne operacije,
ali samo s recima. Vršeći elementarne operacije nad stupcima,
pobrkali bismo nepoznanice do te mjere da više ne bismo znali što
smo na kraju izračunali.
Rang matrice
Neka je
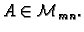 Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
![% latex2html id marker 31185
$\displaystyle A=\left[\begin{array}{cccc}
\boldsy...
...bol{a}_{2\,\cdot} \\ \vdots \\ \boldsymbol{a}_{m\,\cdot}
\end{array} \right],$](img435.gif)
Među vektorima
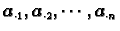 ima određeni broj linearno nezavisnih, i među vektorima
ima određeni broj linearno nezavisnih, i među vektorima
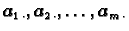 također ima
određeni broj linearno nezavisnih.
također ima
određeni broj linearno nezavisnih.
Teorem 4
Neka je
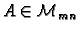
proizvoljna matrica.
- 1.
- Broj linearno nezavisnih stupaca matrice
 se ne mijenja,
ako je pomnožimo s lijeva s elementarnom matricom.
se ne mijenja,
ako je pomnožimo s lijeva s elementarnom matricom.
- 2.
- Broj linearno nezavisnih redaka matrice
 se ne mijenja,
ako je pomnožimo s desna s elementarnom matricom.
se ne mijenja,
ako je pomnožimo s desna s elementarnom matricom.
Dokaz. 1. Neka je 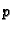 broj
linearno nezavisnih stupaca matrice
broj
linearno nezavisnih stupaca matrice 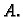 Radi jednostavnosti
pretpostavimo da su to prvih
Radi jednostavnosti
pretpostavimo da su to prvih 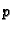 stupaca
stupaca
Neka je 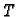 elementarna matrica. Tada je
Ispitajmo linearnu nezavisnost prvih
elementarna matrica. Tada je
Ispitajmo linearnu nezavisnost prvih 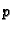 stupaca u tako
dobivenoj matrici.
Matrica
stupaca u tako
dobivenoj matrici.
Matrica
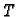 je regularna, postoji
je regularna, postoji 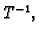 pa je
odakle, zbog
linearne nezavisnosti vektora
pa je
odakle, zbog
linearne nezavisnosti vektora
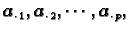 slijedi
slijedi
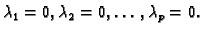 Prema tome prvih
Prema tome prvih 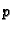 stupaca matrice
stupaca matrice 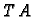 je
linearno nezavisno. Tako smo dokazali da se broj linearno nezavisnih
stupaca matrice
je
linearno nezavisno. Tako smo dokazali da se broj linearno nezavisnih
stupaca matrice  ne smanjuje nakon množenja s elementarnom
matricom s lijeva.
ne smanjuje nakon množenja s elementarnom
matricom s lijeva.
Taj broj se ne može niti
uvećati, što pokazuje sljedeće razmatranje. Neka su stupci
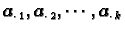 matrice
matrice
 linearno zavisni. To znači da vrijedi
za barem jedan
linearno zavisni. To znači da vrijedi
za barem jedan
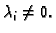 Tada je
i pri
tom je barem jedan
Tada je
i pri
tom je barem jedan
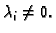 Prema tome i vektori
Prema tome i vektori
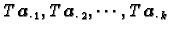 su linearno zavisni.
su linearno zavisni.
2. Ako produkt 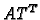 transponiramo, dobivamo
transponiramo, dobivamo 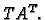 Kao u prvom dijelu dokaza imamo da
se broj linearno nezavisnih stupaca u
Kao u prvom dijelu dokaza imamo da
se broj linearno nezavisnih stupaca u 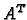 nije promijenio. No, to
znači da se broj linearno nezavisnih redaka u matrici
nije promijenio. No, to
znači da se broj linearno nezavisnih redaka u matrici  nije
promijenio.
nije
promijenio.
Teorem 5
(Teorem o rangu).
Broj linearno nezavisnih redaka proizvoljne matrice

tipa
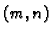
jednak je broju njezinih linearno nezavisnih stupaca. Taj broj se
zove
rang
matrice 
, i označava se sa
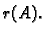
Dokaz. Množeći matricu  dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica
dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica  se može svesti na oblik
se može svesti na oblik
gdje je  jedinica na dijagonali. Stupci (reci) u
kojima se pojavljuju jedinice su
linearno nezavisni. Dokaz je isti kao dokaz linearne nezavisnosti
kanonske baze (primjer 1.7). Ako tim stupcima
(recima) dodamo stupac (redak) sastavljen od samih nula, stupci
(reci) će postati linearno zavisni, jer množeći taj stupac
(redak) s
jedinica na dijagonali. Stupci (reci) u
kojima se pojavljuju jedinice su
linearno nezavisni. Dokaz je isti kao dokaz linearne nezavisnosti
kanonske baze (primjer 1.7). Ako tim stupcima
(recima) dodamo stupac (redak) sastavljen od samih nula, stupci
(reci) će postati linearno zavisni, jer množeći taj stupac
(redak) s 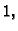 a druge s nulom, dobivamo nulstupac (nulredak).
Tako imamo
a druge s nulom, dobivamo nulstupac (nulredak).
Tako imamo 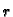 linearno nezavisnih stupaca i također
linearno nezavisnih stupaca i također 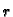 linearno
nezavisnih redaka. Time smo dokazali teorem o rangu.
linearno
nezavisnih redaka. Time smo dokazali teorem o rangu.
Dokazom ovog teorema smo ujedno dobili metodu za ispitivanje ranga
matrice. Treba elementarnim operacijama svesti matricu na oblik kao u
dokazu teorema, i zatim očitati broj jedinica na dijagonali.
Primjer 1.14
Treba naći rang matrice
Rješenje.
pa je prema tome
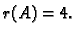
Primjer 1.15
Odrediti rang slijedeće matrice u ovisnosti o
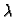
Rješenje. Najprije zamjenom redaka i stupaca imamo
Sada množenjem prvog retka redom s
i
i dodavanjem trećem i
četvrtom retku dobivamo
Množenjem prvog stupca s odgovarajućim brojevima i dodavanjem
ostalim stupcima možemo u prvom retku dobiti same nule. Budući da su
u ostalim recima prvog stupca nule, to neće imati nikakvog utjecaja
na elemente u ostalim recima. Zato smijemo jednostavno u prvom retku
upisati nule. Zatim pomnožimo četvrti redak redom s
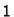
i s
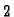
i
dodamo drugom i trećem retku. Nakon toga četvrti redak preselimo na
mjesto drugog.
Sada s drugim stupcem možemo anulirati elemente u drugom retku, a da
se ništa drugo ne promijeni. Tako imamo konačno
Korijeni polinoma
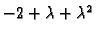
su
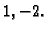
Prema tome, ako je
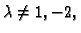
rang je
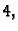
ako je
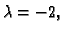
rang je
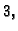
ako je
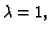
rang je
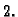
Inverzna matrica
Primijetimo najprije da je u dokazu teorema 4 korišteno
samo svojstvo regularnosti matrice 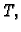 tako da teorem vrijedi i u
slučaju da je
tako da teorem vrijedi i u
slučaju da je 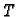 bilo koja regularna matrica. Budući da za
regularnu kvadratnu matricu
bilo koja regularna matrica. Budući da za
regularnu kvadratnu matricu  vrijedi
vrijedi
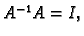 i da množenje s
regularnom matricom
i da množenje s
regularnom matricom 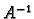 ne mijenja rang (broj linearno nezavisnih
redaka ili stupaca), slijedi da su stupci (reci) regularne matrice
linearno nezavisni. Također vrijedi i obrat. Ako su stupci (reci)
kvadratne matrice linearno nezavisni, onda je matrica
regularna. Dakle, vrijedi sljedeća tvrdnja.
ne mijenja rang (broj linearno nezavisnih
redaka ili stupaca), slijedi da su stupci (reci) regularne matrice
linearno nezavisni. Također vrijedi i obrat. Ako su stupci (reci)
kvadratne matrice linearno nezavisni, onda je matrica
regularna. Dakle, vrijedi sljedeća tvrdnja.
Neka je  kvadratna regularna matrica. Gauss-Jordanovom
metodom, odnosno množenjem s lijeva s elementarnim matricama
kvadratna regularna matrica. Gauss-Jordanovom
metodom, odnosno množenjem s lijeva s elementarnim matricama
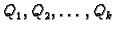 svedemo
svedemo  na
na 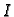
Tada je
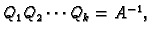 i prema tome
Ova formula nam daje postupak za invertiranje matrice. Taj postupak se
sastoji u tome da formiramo pravokutnu matricu tako da matrici
i prema tome
Ova formula nam daje postupak za invertiranje matrice. Taj postupak se
sastoji u tome da formiramo pravokutnu matricu tako da matrici
 dodamo jediničnu matricu
dodamo jediničnu matricu 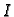 istog reda, i zatim elementarnim
operacijama nad recima prvi dio pravokutne matrice (onaj gdje se
prvobitno nalazila matrica
istog reda, i zatim elementarnim
operacijama nad recima prvi dio pravokutne matrice (onaj gdje se
prvobitno nalazila matrica  ) svedemo na jediničnu matricu. U
drugom dijelu pravokutne matrice se tada nalazi
) svedemo na jediničnu matricu. U
drugom dijelu pravokutne matrice se tada nalazi 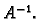
Primjer 1.16
Treba invertirati matricu
Rješenje.
Odatle
Množenjem se lako može provjeriti da je to
doista inverzna matrica matrice
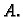
Kronecker-Capellijev teorem
Teorem 7
(Kronecker-Capelli).
Sustav linearnih algebarskih jednadžbi ima bar jedno rješenje, ako
i samo ako je rang matrice sustava jednak rangu proširene matrice
sustava.
Dokaz. Sustav
možemo shvatiti kao jednakost dva vektorstupca
što se može napisati i ovako
Na ovaj način zapisani sustav pokazuje da postoji rješenje sustava,
ako i samo ako se desna strana može prikazati kao linearna kombinacija
stupaca matrice sustava. U tom slučaju je desna strana linearno
zavisna od stupaca matrice sustava, tj. rang proširene matrice
sustava jednak je rangu matrice sustava. Iz ovog zapisa se vidi da je
svaka uređena  -torka koeficijenata linearne kombinacije koja daje
desnu stranu rješenje sustava.
-torka koeficijenata linearne kombinacije koja daje
desnu stranu rješenje sustava.
Iz zapisa sustava kao u dokazu teorema se vidi još nešto. Ako sustav
ima rješenja i ako su stupci matrice sustava  linearno nezavisni,
onda se desna strana može napisati kao linearna kombinacija stupaca
matrice
linearno nezavisni,
onda se desna strana može napisati kao linearna kombinacija stupaca
matrice  i to na jedinstven način (dokaz jedinstvenosti kao kod
dokaza jedinstvenosti prikaza vektora u bazi: teorem
2). U tom slučaju koeficijenti linearne
kombinacije čine rješenje i to jedinstveno.
i to na jedinstven način (dokaz jedinstvenosti kao kod
dokaza jedinstvenosti prikaza vektora u bazi: teorem
2). U tom slučaju koeficijenti linearne
kombinacije čine rješenje i to jedinstveno.
Primjer 1.17
Neka je dan sustav
Stupci matrice sustava su vektori
Oni su linearno nezavisni, ima ih tri, i kako su duljine tri, prema
teoremu
3 oni čine bazu u vektorskom prostoru
radijvektora u prostoru. Prema tome (v. teorem
2), vektor desne strane
se može na jedinstven
način prikazati kao linearna kombinacija vektora
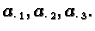
Rješenje sustava je uređena
trojka koeficijenata linearne kombinacije. Kako je
rješenje sustava je
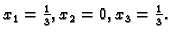
Ako desna strana linearno zavisi od stupaca matrice sustava, i ako su
stupci matrice  linearno zavisni, onda se desna strana može na
više načina prikazati kao linearna kombinacija stupaca matrice. U
tom slučaju postoje brojevi
linearno zavisni, onda se desna strana može na
više načina prikazati kao linearna kombinacija stupaca matrice. U
tom slučaju postoje brojevi
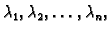 od kojih je bar jedan različit od nule, tako da je
od kojih je bar jedan različit od nule, tako da je
pa je
Tako imamo više rješenja.
Primjer 1.18
Neka je dan sustav
Stupci matrice sustava su linearno zavisni. Ipak njihova linearna
kombinacija s koeficijentima
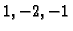
daje desnu stranu. Međutim to
nije jedina linearna kombinacija koja daje desnu stranu. Desnu stranu
daju također linearne kombinacije s koeficijentima
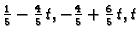
za bilo koji
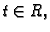
što se lako može provjeriti.
Konačno, ako desna strana nije linearno zavisna od
stupaca matrice, onda ne postoji linearna kombinacija stupaca matrice
 koja bi dala desnu stranu, pa je sustav nekonzistentan.
koja bi dala desnu stranu, pa je sustav nekonzistentan.
Primjer 1.19
Neka je dan sustav
Stupci matrice sustava su linearno zavisni. Na pr. treći stupac je
linearna kombinacija prva dva s koeficijentima
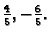
Prema tome skup svih vektora koji su linearne
kombinacije sva tri stupca matrice sustava (vektorski prostor razapet
sa stupcima matrice) se podudara sa skupom svih vektora koji su
linearne kombinacije samo prva dva stupca matrice sustava (vektorski
prostor razapet s prva dva stupca). Ako vektorstupce identificiramo s
radijvektorima, onda to znači da prva dva stupca (radijvektora)
razapinju u prostoru ravninu (zapravo dvodimenzionalni vektorski
prostor radijvektora, koji se nalaze u prostoru, ali leže u jednoj
ravnini). Ne postoji takva linearna kombinacija prva dva stupca koja
daje desnu stranu. To znači da pripadni radijvektor (desne strane)
ne leži u ravnini razapetoj s radijvektorima prva dva
stupca. Da bismo se u to uvjerili, nađimo jednadžbu ravnine razapete
s prva dva stupca. Radijvektori mogu razapinjati samo ravnine kroz
ishodište, pa je
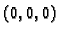
točka kojom prolazi ravnina. Zatim,
vektor normale je vektorski produkt vektora koji razapinju ravninu,
dakle
Prema tome jednadžba ravnine je
Samo ona desna strana (koordinate točke u prostoru, vrh radijvektora
u prostoru) koja zadovoljava ovu jednadžbu, jeste nekakva linearna
kombinacija stupaca matrice sustava. Lako se vidi da desna strana u
ovom primjeru ne zadovoljava jednadžbu ravnine, dok je desna strana
iz primjera
1.18 zadovoljava.
Struktura skupa svih rješenja
Pretpostavimo da matrica sustava
ima isti rang kao proširena matrica sustava, i to 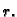 To znači da
proširena matrica sustava
To znači da
proširena matrica sustava 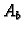 ima linearno nezavisnih
ima linearno nezavisnih 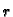 redaka i
redaka i
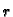 stupaca. Radi jednostavnosti pretpostavimo da je prvih
stupaca. Radi jednostavnosti pretpostavimo da je prvih 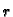 redaka
i prvih
redaka
i prvih 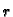 stupaca marice
stupaca marice 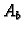 linearno nezavisno. Tada
Gauss-Jordanovom metodom možemo sustav svesti na oblik
Odatle čitamo
linearno nezavisno. Tada
Gauss-Jordanovom metodom možemo sustav svesti na oblik
Odatle čitamo
tako da se rješenje, odnosno skup svih rješenja može napisati u obliku
Stavimo
Svako rješenje
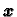 ima oblik
Pretpostavimo da je sustav na početku bio homogen, tj. da je bilo
ima oblik
Pretpostavimo da je sustav na početku bio homogen, tj. da je bilo
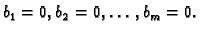 U tom slučaju na isti način
dobivamo rješenje
Skup svih takvih vektora,
kada parametri
U tom slučaju na isti način
dobivamo rješenje
Skup svih takvih vektora,
kada parametri
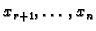 uzimaju proizvoljne realne
vrijednosti nezavisno jedan od drugog, predstavlja skup svih rješenja
pripadnog homogenog sustava. Uočimo da je taj skup vektorski prostor
razapet s vektorima
uzimaju proizvoljne realne
vrijednosti nezavisno jedan od drugog, predstavlja skup svih rješenja
pripadnog homogenog sustava. Uočimo da je taj skup vektorski prostor
razapet s vektorima
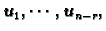 i da su vektori
i da su vektori
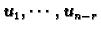 linearno nezavisni, pa prema tome čine bazu
u tom vektorskom prostoru. S druge strane
linearno nezavisni, pa prema tome čine bazu
u tom vektorskom prostoru. S druge strane
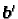 je jedno rješenje
nehomogenog sustava, i to kad stavimo
je jedno rješenje
nehomogenog sustava, i to kad stavimo
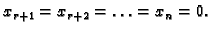 Tako vidimo da se skup svih rješenja sustava može dobiti
tako da se nađe jedno rješenje nehomogenog sustava, to rješenje
zovemo partikularnim, i da se
zatim nađe neka baza vektorskog prostora svih rješenja pripadnog
homogenog sustava. Jedna od tih baza je
Tako vidimo da se skup svih rješenja sustava može dobiti
tako da se nađe jedno rješenje nehomogenog sustava, to rješenje
zovemo partikularnim, i da se
zatim nađe neka baza vektorskog prostora svih rješenja pripadnog
homogenog sustava. Jedna od tih baza je
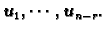
Ova diskusija omogućava da se u jednostavnijim slučajevima 'vidi' skup svih rješenja, što je sadržaj sljedećeg primjera.
Primjer 1.20
Razmotrimo ponovno primjer
1.18. U tom slučaju je rang matrice sustava jednak rangu proširene matrice, i iznosi
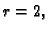
dok je
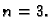
Osim toga je treći stupac linearna kombinacija prva dva. Dakle, svako rješenje je oblika
odnosno
To se može drukčije napisati ovako
što predstavlja parametarske jednadžbe pravca u prostoru. Prvi
stupac desno od jednakosti čine koordinate točke kojom pravac
prolazi, a drugi stupac čine komponente vektora smjera pravca.
Rješenja su dakle točke na pravcu (slika
1.13) u prostoru
(radijvektori u prostoru, čiji vrhovi leže na jednom pravcu).
Rješenje pripadnog homogenog sustava se dobije tako da se izbaci prvi
stupac desno od jednakosti (vektor
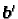
). U tom slučaju su
rješenja točke na pravcu kroz ishodište, koji je paralelan gornjem
pravcu.
Slika 1.13:
Jednoparametarsko rješenje sustava linearnih algebarskih jednadžbi.
Kako su u gornjem sustavu samo dvije
jednadžbe linearno nezavisne, i budući da svaka od njih predstavlja
jednadžbu ravnine u prostoru, rješavanje ovog sustava se zapravo
svodi na to da se želi dobiti jednadžba pravca u prostoru koji je
zadan kao presjek dviju ravnina.
Primjer 1.21
Ako se sustav sastoji od dvije ili više jednadžbi s tri
nepoznanice, od kojih je samo jedna linearno nezavisna, onda to
znači da su ostale jednadžbe multipli prve. Kako je prva
jednadžba linearna, skup točaka koji je zadovoljava predstavlja
ravninu u prostoru. Dakle, skup svih rješenja takvog sustava je
skup radijvektora (vektorstupaca), čiji vrhovi leže u ravnini u
prostoru koja je zadana bilo kojom od jednadnadžbi sustava (slika
1.14). U pripadnom homogenom sustavu je i dalje samo
jedna (bilo koja) jednadžba linearno nezavisna, pa kao rješenje
homogenog sustava imamo također ravninu, paralelnu prethodnoj, ali
koja prolazi ishodištem.
Slika 1.14:
Dvoparametarsko rješenje sustava linearnih algebarskih jednadžbi.
Ako s 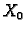 označimo skup svih rješenja pripadnog homogenog,
a s
označimo skup svih rješenja pripadnog homogenog,
a s 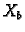 skup svih rješenja nehomogenog sustava, onda je
skup svih rješenja nehomogenog sustava, onda je 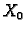 vektorski prostor dimenzije
vektorski prostor dimenzije 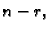 gdje je
gdje je 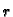 rang matrice sustava, i
vrijedi
rang matrice sustava, i
vrijedi
gdje
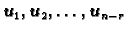 čine bazu u
čine bazu u 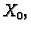 a
a
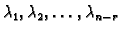 su proizvoljni brojevi. Također vrijedi
su proizvoljni brojevi. Također vrijedi
Primjer 1.22
Riješiti sustav jednadžbi
Rješenje. Rješenje ovog sustava je svaka uređena petorka (vektorstupac)
koja zadovoljava svaku jednadžbu.
Gauss-Jordanovim postupkom dolazimo do sustava
Odatle,
pa je rješenje
Pri tom je
![% latex2html id marker 31704
$ \left[ \begin{array}{r}
-1 \\ 1 \\ 0 \\ 0 \\ 0
\end{array} \right]$](img570.gif)
partikularno rješenje, a vektori
![% latex2html id marker 31706
$ \left[ \begin{array}{r}
-1 \\ -1 \\ 1 \\ 0 \\ ...
...ght],\;
\left[ \begin{array}{r}
-1 \\ -2 \\ 0 \\ 0 \\ 1
\end{array} \right]$](img571.gif)
čine bazu u vektorskom prostoru svih rješenja
pripadnog homogenog sustava.
Primjer 1.23
Diskutirati i riješiti sljedeći sustav jednadžbi u odnosu na
parametar
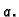
Rješenje. Proširena matrica sustava je
Množimo prvi redak redom s
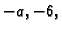
i dodamo drugom, odnosno trećem
retku. Zatim tako dobiveni drugi redak dodamo trećem. Konačno prvim
stupcem anuliramo elemente u prvom retku. Dobijemo
Sada
ne smijemo s drugim stupcem anulirati
elemente u drugom retku, jer se može dogoditi da je
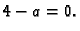
S
elementarnim transformacijama smo gotovi, i treba provesti diskusiju.
Ako je 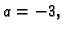 onda je
onda je
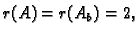 pa imamo beskonačno mnogo
rješenja (jednoparametarsko rješenje). Da dobijemo rješenje u tom
slučaju, moramo se vratiti korak natrag, prije anuliranja elemenata u
prvom retku, i uvrstiti
pa imamo beskonačno mnogo
rješenja (jednoparametarsko rješenje). Da dobijemo rješenje u tom
slučaju, moramo se vratiti korak natrag, prije anuliranja elemenata u
prvom retku, i uvrstiti 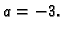
Zatim pomnožiti drugi redak s
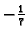
i dodati ga prvom.
Odatle se čita rješenje
Ako je 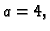 onda je
onda je
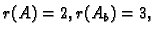 pa ne postoji rješenje.
pa ne postoji rješenje.
Inače je
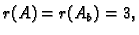 i tada imamo jedinstveno rješenje, koje
dobijemo nakon Gaussovog postupka.
i tada imamo jedinstveno rješenje, koje
dobijemo nakon Gaussovog postupka.
Iz zadnje jednadžbe čitamo da je
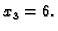
Uvrštavanjem u drugu
dobijemo
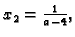
i konačno iz prve jednadžbe slijedi
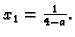




Next: Problem vlastitih ...
Up: Matrice i sustavi jednadžbi
Previous: Vektori i matrice
Contents
Index
Salih Suljagic
1999-12-17
![]() jednadžbi s
jednadžbi s ![]() nepoznanica oblika
nepoznanica oblika
![\begin{displaymath}
% latex2html id marker 30925
A=
\left[
\begin{array}{cccc}
...
...
a_{m1} & a_{m2} & \cdots & a_{mn} & b_m
\end{array}\right].\end{displaymath}](img371.gif)
![]() -torka brojeva
-torka brojeva
![]() koja zadovoljava svaku od jednadžbi u
sustavu. Sustav može imati jedno rješenje, više rješenja i niti
jedno rješenje. Ako ne postoji rješenje onda kažemo da je sustav
nekonzistentan ili
nemoguć ili
protuslovan.
koja zadovoljava svaku od jednadžbi u
sustavu. Sustav može imati jedno rješenje, više rješenja i niti
jedno rješenje. Ako ne postoji rješenje onda kažemo da je sustav
nekonzistentan ili
nemoguć ili
protuslovan.
![]() -torka
-torka
![]() rješenje. To rješenje se zove trivijalno. Pravi
problem kod homogenih sustava je da li postoje rješenja različita od
trivijalnog, tj. da li postoje netrivijalna rješenja.
rješenje. To rješenje se zove trivijalno. Pravi
problem kod homogenih sustava je da li postoje rješenja različita od
trivijalnog, tj. da li postoje netrivijalna rješenja.
![]() u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz
u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz ![]() pomnožimo brojem koji je suprotan
koeficijentu uz
pomnožimo brojem koji je suprotan
koeficijentu uz ![]() u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz
u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz ![]() pomnožimo brojem koji je suprotan koeficijentu uz
pomnožimo brojem koji je suprotan koeficijentu uz ![]() u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz
u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz ![]() pomnožimo brojem koji je
suprotan koeficijentu uz
pomnožimo brojem koji je
suprotan koeficijentu uz ![]() u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili
u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili ![]() iz
druge, treće,
iz
druge, treće, ![]()
![]() -te jednadžbe i došli do ekvivalentnog
sustava oblika
-te jednadžbe i došli do ekvivalentnog
sustava oblika
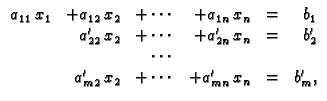
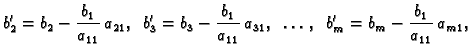
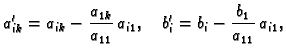 za
za
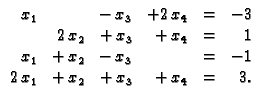
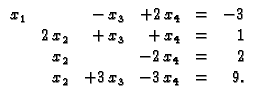
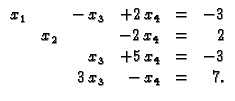
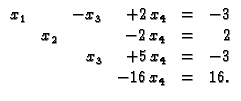
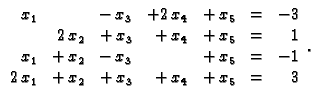
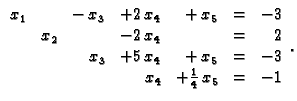
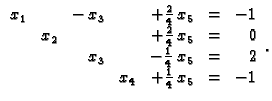
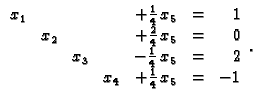
![]() kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za
kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za ![]() pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja.
pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja. ![]() može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.
može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.
![]() točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih
točaka na štapu, koje ćemo zvati čvorovi.
Promatrat ćemo štap kao da je njegova masa koncentrirana u tih ![]() točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
točaka. Prema tome pretpostavljamo da sile mogu djelovati samo u
čvorovima. Shodno tome i progib promatramo samo u čvorovima. Pri tom
polazimo od dvije osnovne pretpostavke, koje u fizici predstavljaju
princip superpozicije sila, a u matematici se
to zove svojstvo
linearnosti.
![]() progib u čvoru
progib u čvoru ![]() uslijed djelovanja jedinične
sile u čvoru
uslijed djelovanja jedinične
sile u čvoru ![]() (sl. 1.10).
(sl. 1.10).
![]() djeluje sila
djeluje sila ![]() takva da
poništava utjecaj jedinične sile u čvoru
takva da
poništava utjecaj jedinične sile u čvoru ![]() na čvor
na čvor ![]()
![]() dobivena iz matrice
dobivena iz matrice ![]() primjenom jedne ili više
elementarnih operacija, onda pišemo
primjenom jedne ili više
elementarnih operacija, onda pišemo
![% latex2html id marker 31134
$\displaystyle \left[\begin{array}{rrrr}
1 & 0 & 0 ...
...}
1 & 0 & -1 \\
1 & 1 & -1 \\
0 & 2 & 1 \\
2 & 1 & 1
\end{array} \right],$](img424.gif)
![% latex2html id marker 31136
$\displaystyle \left[ \begin{array}{rrr}
1 & 0 & -1...
...}
1 & -1 & 0 \\
0 & 1 & 2 \\
1 & -1 & 1 \\
2 & 1 & 1
\end{array} \right].$](img425.gif)
![% latex2html id marker 31139
$\displaystyle \left[\begin{array}{rrrr}
1 & 0 & 0 ...
...}
1 & 0 & -1 \\
0 & 2 & 1 \\
3 & 3 & -3 \\
2 & 1 & 1
\end{array} \right],$](img426.gif)
![% latex2html id marker 31141
$\displaystyle \left[ \begin{array}{rrr}
1 & 0 & -1...
...}
1 & 0 & -1 \\
0 & 6 & 1 \\
1 & 3 & -1 \\
2 & 3 & 1
\end{array} \right].$](img427.gif)
![]() (različitim od nule), dobili smo
matricu u kojoj je treći redak pomnožen brojem
(različitim od nule), dobili smo
matricu u kojoj je treći redak pomnožen brojem ![]()
![]() (različitim od nule), dobili smo
matricu u kojoj je drugi stupac pomnožen brojem
(različitim od nule), dobili smo
matricu u kojoj je drugi stupac pomnožen brojem ![]()
![% latex2html id marker 31152
$\displaystyle \left[\begin{array}{rrrr}
1 & 0 & 0 ...
...}
1 & 0 & -1 \\
0 & 2 & 1 \\
1 & 1 & -1 \\
0 & 1 & 3
\end{array} \right],$](img430.gif)
![% latex2html id marker 31154
$\displaystyle \left[ \begin{array}{rrr}
1 & 0 & -1...
...
3 & 0 & -1 \\
-2 & 2 & 1 \\
3 & 1 & -1 \\
0 & 1 & 1
\end{array} \right].$](img431.gif)
![]() i dodali četvrtom, dobili smo
matricu u kojoj je prvi redak pomnožen brojem
i dodali četvrtom, dobili smo
matricu u kojoj je prvi redak pomnožen brojem ![]() dodan
četvrtom retku.
dodan
četvrtom retku.
![]() i dodali prvom, dobili smo matricu u
kojoj je treći stupac pomnožen brojem
i dodali prvom, dobili smo matricu u
kojoj je treći stupac pomnožen brojem ![]() dodan prvom stupcu.
dodan prvom stupcu.![]() pomnožimo s lijeva (s
desna) s jediničnom matricom u kojoj je treći redak (stupac)
pomnožen brojem
pomnožimo s lijeva (s
desna) s jediničnom matricom u kojoj je treći redak (stupac)
pomnožen brojem
![]() dobit ćemo jediničnu matricu. Ako
jediničnu matricu u kojoj je trećem retku (stupcu) dodan prvi
pomnožen s
dobit ćemo jediničnu matricu. Ako
jediničnu matricu u kojoj je trećem retku (stupcu) dodan prvi
pomnožen s ![]() pomnožimo s lijeva (s desna) s jediničnom matricom
u kojoj je trećem retku (stupcu) dodan prvi pomnožen s
pomnožimo s lijeva (s desna) s jediničnom matricom
u kojoj je trećem retku (stupcu) dodan prvi pomnožen s ![]() dobit
ćemo jediničnu matricu.
dobit
ćemo jediničnu matricu.
![]() Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
Njezine stupce, i njezine retke možemo
shvatiti kao vektore.
![% latex2html id marker 31185
$\displaystyle A=\left[\begin{array}{cccc}
\boldsy...
...bol{a}_{2\,\cdot} \\ \vdots \\ \boldsymbol{a}_{m\,\cdot}
\end{array} \right],$](img435.gif)
![]() broj
linearno nezavisnih stupaca matrice
broj
linearno nezavisnih stupaca matrice ![]() Radi jednostavnosti
pretpostavimo da su to prvih
Radi jednostavnosti
pretpostavimo da su to prvih ![]() stupaca
stupaca
![]() dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica
dovoljan (konačan) broj puta s lijeva i s desna s odgovarajućim
elementernim matricama, matrica ![]() se može svesti na oblik
se može svesti na oblik
![% latex2html id marker 31275
$\displaystyle \left[\begin{array}{cccccc}
1 & \cd...
...dots & \ddots & \vdots \\
0 & \cdots & 0 & 0 & \cdots & 0
\end{array}\right],$](img461.gif)
![% latex2html id marker 31288
$\displaystyle A=\left[ \begin{array}{rrrrrr}
1 & 0...
...& 1 \\
1 & 1 & -1 & 0 & 1 & -1 \\
2 & 1 & 1 & 1 & 1 & 3
\end{array}\right].$](img465.gif)
![% latex2html id marker 31290
$\displaystyle \left[ \begin{array}{rrrrrr}
1 & 0 &...
...0 & 0 & 1 & 5 & 1 & -3 \\
0 & 0 & 0 & 1 &\frac{1}{4} & -1
\end{array} \right]$](img466.gif)
![% latex2html id marker 31292
$\displaystyle \sim\left[\begin{array}{rrrrrr}
1 & ...
... & 0 \\
0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0
\end{array} \right],$](img467.gif)
![% latex2html id marker 31299
$\displaystyle A = \left[\begin{array}{rrrr}
1-\lam...
...lambda+\lambda^2 & -2+2\lambda-\lambda^2-\lambda^3 & 2 & 5
\end{array}\right].$](img469.gif)
![% latex2html id marker 31301
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 &...
...2+3\lambda+\lambda^2 & -2+2\lambda-\lambda^2-\lambda^3 \\
\end{array}\right].$](img470.gif)
![% latex2html id marker 31307
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 &...
... & -2+\lambda+\lambda^2 & 2\lambda-\lambda^2-\lambda^3 \\
\end{array}\right].$](img471.gif)
![% latex2html id marker 31313
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 &...
...& -1+\lambda & 0 \\
0 & 0 & 0 & -2+\lambda+\lambda^2 \\
\end{array}\right].$](img473.gif)
![% latex2html id marker 31315
$\displaystyle A \sim \left[\begin{array}{rrrr}
1 &...
...& -1+\lambda & 0 \\
0 & 0 & 0 & -2+\lambda+\lambda^2 \\
\end{array}\right].$](img474.gif)
![]() tako da teorem vrijedi i u
slučaju da je
tako da teorem vrijedi i u
slučaju da je ![]() bilo koja regularna matrica. Budući da za
regularnu kvadratnu matricu
bilo koja regularna matrica. Budući da za
regularnu kvadratnu matricu ![]() vrijedi
vrijedi
![]() i da množenje s
regularnom matricom
i da množenje s
regularnom matricom ![]() ne mijenja rang (broj linearno nezavisnih
redaka ili stupaca), slijedi da su stupci (reci) regularne matrice
linearno nezavisni. Također vrijedi i obrat. Ako su stupci (reci)
kvadratne matrice linearno nezavisni, onda je matrica
regularna. Dakle, vrijedi sljedeća tvrdnja.
ne mijenja rang (broj linearno nezavisnih
redaka ili stupaca), slijedi da su stupci (reci) regularne matrice
linearno nezavisni. Također vrijedi i obrat. Ako su stupci (reci)
kvadratne matrice linearno nezavisni, onda je matrica
regularna. Dakle, vrijedi sljedeća tvrdnja.
![]() kvadratna regularna matrica. Gauss-Jordanovom
metodom, odnosno množenjem s lijeva s elementarnim matricama
kvadratna regularna matrica. Gauss-Jordanovom
metodom, odnosno množenjem s lijeva s elementarnim matricama
![]() svedemo
svedemo ![]() na
na ![]()
![% latex2html id marker 31380
$\displaystyle A=\left[\begin{array}{rrrr}
1 & 1 & ...
...1 \\
1 & 2 & 2 & 2 \\
1 & 2 & 3 & 3 \\
1 & 2 & 3 & 4
\end{array}\right].$](img491.gif)
![% latex2html id marker 31382
$\displaystyle \left[\begin{array}{rrrrrrrr}
1 & 1 ...
... 2 & 2 & -1 & 0 & 1 & 0 \\
0 & 1 & 2 & 3 & -1 & 0 & 0 & 1
\end{array}\right]$](img492.gif)
![% latex2html id marker 31384
$\displaystyle \sim\left[\begin{array}{rrrrrrrr}
1 ...
... 1 & 1 & 0 & -1 & 1 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & -1 & 1
\end{array}\right]$](img493.gif)
![% latex2html id marker 31386
$\displaystyle \sim\left[\begin{array}{rrrrrrrr}
1 ...
...1 & 0 & 0 & -1 & 2 & -1 \\
0 & 0 & 0 & 1 & 0 & 0 & -1 & 1
\end{array}\right]$](img494.gif)
![% latex2html id marker 31388
$\displaystyle \sim\left[\begin{array}{rrrrrrrr}
1 ...
... & 0 & 0 & -1 & 2 & -1 \\
0 & 0 & 0 & 1 & 0 & 0 & -1 & 1
\end{array}\right].$](img495.gif)
![% latex2html id marker 31390
$\displaystyle A^{-1}=\left[\begin{array}{rrrr}
2 &...
...
-1 & 2 & -1 & 0 \\
0 & -1 & 2 & -1 \\
0 & 0 & -1 & 1
\end{array}\right].$](img496.gif)
![% latex2html id marker 31419
$\displaystyle \left[
\begin{array}{c} a_{11}\,x_1+...
...ft[ \begin{array}{c}
b_{1} \\ b_{2} \\ \vdots \\ b_{m}
\end{array} \right],$](img497.gif)
![% latex2html id marker 31421
$\displaystyle x_1\left[ \begin{array}{c}
a_{11} \...
...ft[ \begin{array}{c}
b_{1} \\ b_{2} \\ \vdots \\ b_{m}
\end{array} \right].$](img498.gif)
![]() linearno nezavisni,
onda se desna strana može napisati kao linearna kombinacija stupaca
matrice
linearno nezavisni,
onda se desna strana može napisati kao linearna kombinacija stupaca
matrice ![]() i to na jedinstven način (dokaz jedinstvenosti kao kod
dokaza jedinstvenosti prikaza vektora u bazi: teorem
2). U tom slučaju koeficijenti linearne
kombinacije čine rješenje i to jedinstveno.
i to na jedinstven način (dokaz jedinstvenosti kao kod
dokaza jedinstvenosti prikaza vektora u bazi: teorem
2). U tom slučaju koeficijenti linearne
kombinacije čine rješenje i to jedinstveno.
![% latex2html id marker 31451
$\displaystyle \boldsymbol{a}_{\cdot\, 1} =
\left[...
...mbol{a}_{\cdot\, 3} =
\left[\begin{array}{c}
4 \\ 2 \\ 2
\end{array}\right].$](img505.gif)
![% latex2html id marker 31453
$\displaystyle \boldsymbol{b}= \left[\begin{array}{c}
3 \\ 1 \\ 1
\end{array}\right]$](img506.gif)
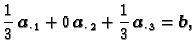
![]() linearno zavisni, onda se desna strana može na
više načina prikazati kao linearna kombinacija stupaca matrice. U
tom slučaju postoje brojevi
linearno zavisni, onda se desna strana može na
više načina prikazati kao linearna kombinacija stupaca matrice. U
tom slučaju postoje brojevi
![]() od kojih je bar jedan različit od nule, tako da je
od kojih je bar jedan različit od nule, tako da je
![]() koja bi dala desnu stranu, pa je sustav nekonzistentan.
koja bi dala desnu stranu, pa je sustav nekonzistentan.
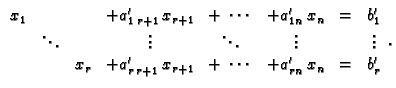
![% latex2html id marker 31587
$\displaystyle \left[\begin{array}{c}
x_1 \\ \vdot...
...{c}
-a'_{1n} \\ \vdots \\ -a'_{rn} \\ 0 \\ \vdots \\ 1 \end{array}\right].$](img532.gif)
![% latex2html id marker 31589
$\displaystyle \boldsymbol{x}= \left[\begin{array}{...
...{c}
-a'_{1n} \\ \vdots \\ -a'_{rn} \\ 0 \\ \vdots \\ 1
\end{array}\right].$](img533.gif)
![% latex2html id marker 31618
$\displaystyle \left[
\begin{array}{c}
x_1 \\ x_2 ...
...,\left[
\begin{array}{c}
-\frac{4}{5} \\ \frac{6}{5} \\ 1
\end{array}\right].$](img546.gif)
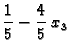
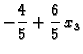
![]() označimo skup svih rješenja pripadnog homogenog,
a s
označimo skup svih rješenja pripadnog homogenog,
a s ![]() skup svih rješenja nehomogenog sustava, onda je
skup svih rješenja nehomogenog sustava, onda je ![]() vektorski prostor dimenzije
vektorski prostor dimenzije ![]() gdje je
gdje je ![]() rang matrice sustava, i
vrijedi
rang matrice sustava, i
vrijedi
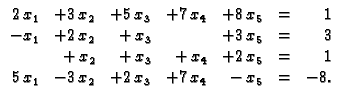
![% latex2html id marker 31674
$\displaystyle \boldsymbol{x}= \left[ \begin{array}{r}
x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5
\end{array} \right],$](img563.gif)
![% latex2html id marker 31702
$\displaystyle \boldsymbol{x}=\left[ \begin{array}{...
...t]+x_5
\left[ \begin{array}{r}
-1 \\ -2 \\ 0 \\ 0 \\ 1
\end{array} \right].$](img569.gif)
![% latex2html id marker 31704
$ \left[ \begin{array}{r}
-1 \\ 1 \\ 0 \\ 0 \\ 0
\end{array} \right]$](img570.gif) partikularno rješenje, a vektori
partikularno rješenje, a vektori
![% latex2html id marker 31706
$ \left[ \begin{array}{r}
-1 \\ -1 \\ 1 \\ 0 \\ ...
...ght],\;
\left[ \begin{array}{r}
-1 \\ -2 \\ 0 \\ 0 \\ 1
\end{array} \right]$](img571.gif)
![% latex2html id marker 31730
$\displaystyle A_b = \left[
\begin{array}{cccc}
1 & 1 & 1 & 6 \\
a & 4 & 1 & 5 \\
6 & a+2 & 2 & 13 \\
\end{array}\right].$](img578.gif)
![% latex2html id marker 31734
$\displaystyle A_b \sim \left[
\begin{array}{cccc}
...
...\
0 & 4-a & 1-a & 5-6a \\
0 & 0 & -(3+a) & -6(3+a) \\
\end{array}\right].$](img580.gif)
![]() onda je
onda je
![]() pa imamo beskonačno mnogo
rješenja (jednoparametarsko rješenje). Da dobijemo rješenje u tom
slučaju, moramo se vratiti korak natrag, prije anuliranja elemenata u
prvom retku, i uvrstiti
pa imamo beskonačno mnogo
rješenja (jednoparametarsko rješenje). Da dobijemo rješenje u tom
slučaju, moramo se vratiti korak natrag, prije anuliranja elemenata u
prvom retku, i uvrstiti ![]()
![% latex2html id marker 31744
$\displaystyle A_b \sim \left[
\begin{array}{cccc}
1 & 1 & 1 & 6 \\
0 & 7 & 4 & 23 \\
0 & 0 & 0 & 0 \\
\end{array}\right].$](img585.gif)
![% latex2html id marker 31748
$\displaystyle A_b \sim \left[
\begin{array}{cccc}
...
... & \frac{19}{7} \\
0 & 7 & 4 & 23 \\
0 & 0 & 0 & 0 \\
\end{array}\right].$](img587.gif)
![% latex2html id marker 31750
$\displaystyle \left[
\begin{array}{c}
x_1 \\ x_2 ...
...t] + x_3\,\left[
\begin{array}{c}
-\frac{3}{7} \\ -4 \\ 1
\end{array}\right].$](img588.gif)
![]() onda je
onda je
![]() pa ne postoji rješenje.
pa ne postoji rješenje.
![]() i tada imamo jedinstveno rješenje, koje
dobijemo nakon Gaussovog postupka.
i tada imamo jedinstveno rješenje, koje
dobijemo nakon Gaussovog postupka.
![% latex2html id marker 31758
$\displaystyle A_b \sim \left[
\begin{array}{cccc}
...
...\
0 & 4-a & 1-a & 5-6a \\
0 & 0 & -(3+a) & -6(3+a) \\
\end{array}\right].$](img592.gif)