



Next: Sustavi običnih diferencijalnih jednadžbi
Up: Matrice i sustavi jednadžbi
Previous: Sustavi linearnih algebarskih jednadžbi
Contents
Index
Subsections
Vlastite vrijednosti i vlastiti vektori
Definicija 13
Neka je

kvadratna matrica reda
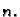
Za broj
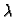
kažemo da
je
vlastita (svojstvena) vrijednost
matrice
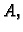
a za vektor
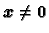
kažemo da je
vlastiti (svojstveni)
vektor matrice
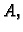
ako vrijedi
Skup svih vlastitih vrijednosti matrice

se zove
spektar matrice
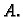
Na slici 1.15 je prikazano nekoliko vektora i njihovih slika
dobivenih djelovanjem matrice
![\begin{displaymath}
% latex2html id marker 31788
\left[
\begin{array}{cc}
2 & -1 \\ -1 & 2
\end{array}\right].\end{displaymath}](img598.gif) Uočite razliku između djelovanja na vektore
Uočite razliku između djelovanja na vektore
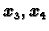 i na ostale vektore. Slike vektora
i na ostale vektore. Slike vektora
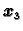 i
i
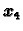 su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
Slika 1.15:
Djelovanje matrice drugog reda na vektore u ravnini.
Neka je
Tada je
također
Dakle, ako je
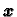 vlastiti vektor za vlastitu vrijednost
vlastiti vektor za vlastitu vrijednost
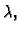 onda je i svaki s njim kolinearan vektor također vlastiti
vektor koji pripada istoj vlastitoj vrijednosti. (Na slici
1.15 su crticama označeni pravci čija svaka točka
predstavlja vrh nekog vlastitog vektora. Na jednom pravcu leže
vlastiti vektori koji pripadaju vlastitoj vrijednosti
onda je i svaki s njim kolinearan vektor također vlastiti
vektor koji pripada istoj vlastitoj vrijednosti. (Na slici
1.15 su crticama označeni pravci čija svaka točka
predstavlja vrh nekog vlastitog vektora. Na jednom pravcu leže
vlastiti vektori koji pripadaju vlastitoj vrijednosti 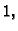 a na drugom
oni koji pripadaju vlastitoj vrijednosti
a na drugom
oni koji pripadaju vlastitoj vrijednosti 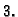 )
)
Jednadžba
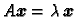 se može
drukčije napisati kao
se može
drukčije napisati kao
Da se nađe
vlastiti vektor, potrebno je riješiti ovu matričnu jednadžbu. Ako
je
![$ A=[a_{ij}],$](img607.gif) i
i
![$ \boldsymbol{x}=[x_i],$](img608.gif) ta jednadžba se može
napisati kao sustav linearnih algebarskih jednadžbi
ta jednadžba se može
napisati kao sustav linearnih algebarskih jednadžbi
Ovo je homogen sustav i on ima netrivijalno
rješenje, ako i samo ako je determinanta sustava jednaka nuli. Dakle,
Ako raspišemo ovu determinantu i jednadžbu pomnožimo s 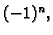 dobivamo algebarsku jednadžbu
dobivamo algebarsku jednadžbu  -tog reda
Ova jednadžba se zove karakteristična jednadžba matrice
-tog reda
Ova jednadžba se zove karakteristična jednadžba matrice 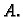 Polinom na
lijevoj strani se zove karakteristični polinom
matrice
Polinom na
lijevoj strani se zove karakteristični polinom
matrice 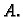 Pri tom je
Pri tom je
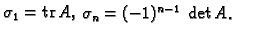
Poznato je da algebarska jednadžba  -tog reda ima
-tog reda ima  općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
Uvrštavanjem pojedinog rješenja u gornji homogeni sustav,
dobivamo sustav jednadžbi koji, zbog toga što je homogen i što je
determinanta jednaka nuli, ima beskonačno mnogo rješenja. To je u
skladu s činjenicom da je svaki vektor, kolinearan s vlastitim
vektorom, također vlastiti. Budući da vlastite vrijednosti mogu biti
kompleksni brojevi, kao rješenja tog sustava možemo dobiti
vektore čije su komponente kompleksni brojevi. Nas će prvenstveno
interesirati slučaj kada su vlastite vrijednosti i vlastiti vektori
realni.
Primjer 1.24
Nađimo vlastite vrijednosti i vlastite vektore matrice
Rješenje. Karakteristična jednadžba je
Vlastite vrijednosti su dakle
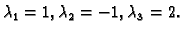
Za
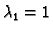 pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
Iz druge jednadžbe imamo
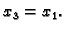
Uvrstimo u treću i dobivamo
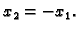
Tako je vlastiti vektor
Za
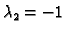
imamo sustav
Rješenja su
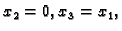
pa je vlastiti vektor
Za
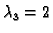
imamo sustav
Rješenja su
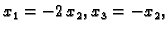
pa je vlastiti vektor
Na slici
1.16 se vide vlastiti vektori i njihove slike.
Slika 1.16:
Vlastiti vektori i njihove slike (različite vlastite vrijednosti).
Prvi vektor je preslikan u samog sebe. Isto se događa sa svakim
drugim radijvektorom, kolinearnim s prvim
vektorom. Drugi se preslika u sebi suprotan, što se događa i sa
svakim s njim kolinearnim radijvektorom. Treći se preslika u
dvostruko dulji (rastegne se), što se događa i sa svakim s njim
kolinearnim radijvektorom. Vektor koji ne leži niti na jednom od
pravaca određenih ovim vektorima, biva preslikan u vektor koji
nije kolinearan sa svojim originalom.
Teorem 8
(Hamilton-Cayley) Ako je polinom
karakteristični polinom matrice
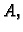
onda je
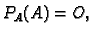
tj.
Dokaz.
Dijagonalizacija simetrične matrice
Kako smo ranije definirali, matrica
![$ A=[a_{ij}]\in{\cal M}_{n}$](img641.gif) je simetrična,
ako je
je simetrična,
ako je 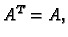 tj. ako je
tj. ako je
Ako je matrica  simetrična, onda vrijedi
simetrična, onda vrijedi
za svaki par vektora
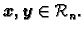
Teorem 9
Vlastite vrijednosti simetrične matrice
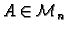
su realni brojevi.
Dokaz. Neka je
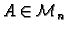 simetrična matrica,
simetrična matrica, 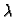 njezina vlastita vrijednost, i
njezina vlastita vrijednost, i
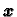 pripadni vlastiti vektor. Tada je
pripadni vlastiti vektor. Tada je
Ako
konjugiramo ovu jednakost, i uzmemo u obzir da je
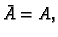 jer su
elementi matrice
jer su
elementi matrice  realni brojevi, dobivamo
Odatle
Zbog
simetričnosti matrice
realni brojevi, dobivamo
Odatle
Zbog
simetričnosti matrice  imamo
Tako je
tj.
Zbog
imamo
Tako je
tj.
Zbog
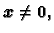 skalarni produkt
skalarni produkt
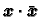 ne može biti jednak nuli,
pa slijedi
ne može biti jednak nuli,
pa slijedi
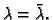
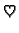
Teorem 10
Vlastiti vektori simetrične matrice
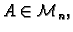
koji pripadaju
različitim vlastitim vrijednostima, su međusobno okomiti.
Dokaz. Neka je 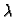 vlastita
vrijednost, i
vlastita
vrijednost, i
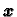 njoj pripadni vlastiti vektor matrice
njoj pripadni vlastiti vektor matrice 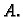 Također, neka je
Također, neka je 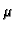 vlastita vrijednost, i
vlastita vrijednost, i
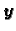 njoj pripadni
vlastiti vektor. Neka je
njoj pripadni
vlastiti vektor. Neka je
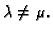 Tada je
Tada je
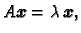 i
i
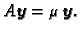 Odatle
Odatle
Zbog simetričnosti matrice  imamo
Tako
je
tj.
Kako je
imamo
Tako
je
tj.
Kako je
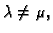 slijedi
tj. vlastiti vektori su
međusobno okomiti.
slijedi
tj. vlastiti vektori su
međusobno okomiti.
Primjer 1.24 pokazuje da ovaj teorem ne vrijedi općenito. U
tom primjeru kosinusi kuteva između vlastitih vektora iznose približno
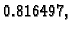
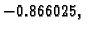
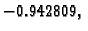 a kutevi u radijanima iznose
približno
a kutevi u radijanima iznose
približno 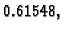
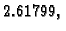
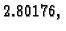 odnosno
odnosno
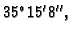
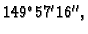
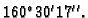
Dijagonalizacija simetrične matrice. Različite vlastite
vrijednosti.
Neka je
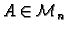 simetrična matrica, i neka su njezine vlastite
vrijednosti
simetrična matrica, i neka su njezine vlastite
vrijednosti
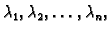 međusobno
različite. Tada
međusobno
različite. Tada  ima
ima  međusobno okomitih vlastitih vektora
međusobno okomitih vlastitih vektora
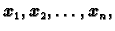 i
vrijedi
i
vrijedi
Neka je
i neka je
![$ X=[x_{ij}]$](img679.gif) matrica, čiji
su stupci vektori
matrica, čiji
su stupci vektori
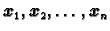 Budući da su njezini stupci međusobno okomiti
vektori, različiti od nulvektora, oni su linearno nezavisni, i prema
tome je matrica
Budući da su njezini stupci međusobno okomiti
vektori, različiti od nulvektora, oni su linearno nezavisni, i prema
tome je matrica 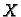 regularna.
regularna.
Imamo
Matrica
![$ [\lambda_j\,\delta_{ij}]$](img684.gif) je dijagonalna s vlasitim vrijednostima
matrice
je dijagonalna s vlasitim vrijednostima
matrice  na glavnoj dijagonali. Ako ovu jednadžbu pomnožimo s
lijeva s
na glavnoj dijagonali. Ako ovu jednadžbu pomnožimo s
lijeva s 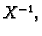 dobivamo
dobivamo
Dijagonalizacija simetrične matrice. Opći slučaj.
U općem slučaju se može dogoditi da neke vlastite vrijednosti budu
višestruke. Razmotrimo sljedeći primjer.
Primjer 1.25
Naći vlastite vrijednosti i vlastite vektore matrice
Rješenje. Vlastite vrijednosti su
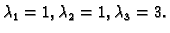
Za
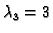 imamo vlastiti vektor
imamo vlastiti vektor
tj. vlastitih vektora ima beskonačno mnogo ali
su svi međusobno kolinearni.
Za
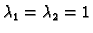 imamo (iz (1.5))
imamo (iz (1.5))
Odavde
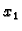
je proizvoljan, i
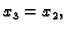
pa je vlastiti vektor
![% latex2html id marker 32119
$\displaystyle \left[\begin{array}{c} x_1 \\ x_2 \...
...{array}\right]+\,x_2\, \left[\begin{array}{c} 0 \\ 1 \\ 1 \end{array}\right],$](img695.gif) |
(1.6) |
tj. vlastitih vektora ima beskonačno mnogo
ali sada su oni linearne kombinacije od dva linearno nezavisna
vektora. Kako imamo slobodu izbora, možemo izabrati bilo koja dva
međusobno okomita vektora, tako da i u slučaju višestrukih
vlastitih vrijednosti imamo međusobno okomite vlastite vektore.
Formula (1.6) se može shvatiti kao parametarske
jednadžbe ravnine u prostoru, koja prolazi ishodištem i razapeta je
vektorima
Dakle svaki radijvektor u toj ravnini je vlastiti, s vlastitom
vrijednošću
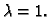
Na slici 1.17 je šatirana ravnina u kojoj je svaki vektor
vlastiti s vlastitom vrijednošću 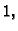 i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću
i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću 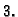
Slika 1.17:
Vlastiti vektori i njihove slike (višestruke vlastite vrijednosti).
Općenito se događa sljedeće. 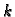 -struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću
-struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću 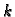 parametara. Izborom ovih
parametara tako da jedan bude
parametara. Izborom ovih
parametara tako da jedan bude 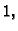 a ostali
a ostali 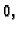 dobivamo
dobivamo 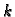 linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo
linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo  linearno nezavisnih vlastitih
vektora simetrične matrice
linearno nezavisnih vlastitih
vektora simetrične matrice 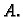 Od njih kao stupaca formiramo matricu
Od njih kao stupaca formiramo matricu
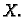 Ona je regularna, i vrijedi
Ona je regularna, i vrijedi
Pomnožimo s lijeva matricom 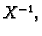 i
dobit ćemo, kao i prije
i
dobit ćemo, kao i prije
Definicija 14
Neka je
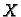
regularna matrica i neka je
Tada
kažemo da su matrice

i
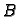 slične
slične.
Ako među matricama sličnim matrici

postoji dijagonalna, onda
kažemo da se matrica

može
dijagonalizirati.
Dijagonalizacija matrice je postupak nalaženja one regularne matrice
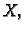
koja ima
svojstvo da je
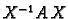
dijagonalna matrica.
U skladu s ovom definicijom, možemo zaključiti da se proizvoljna
simetrična matrica  može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice
može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice 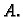
No, i u slučaju višestrukih vlastitih vrijednosti matrica 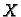 se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
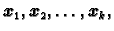 linearno nezavisni vlastiti vektori, onda su vektori
linearno nezavisni vlastiti vektori, onda su vektori
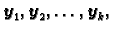 dobiveni po formulama
dobiveni po formulama
međusobno okomiti, i svaki od njih je vlastiti pripadajući istoj
vlastitoj vrijednosti. Ovaj postupak se zove Gram-Schmidtov
postupak ortogonalizacije.
Ideja Gram-Schmidtovog postupka ortogonalizacije je jednostavna i
prirodna. Prvi vektor ostavimo na miru. Njime je određen
pravac. Drugi vektor projiciramo ortogonalno na taj pravac, i zatim
tu projekciju odbijemo od drugog vektora. Time naravno dobivamo vektor
koji je okomit na vektor na koji smo projicirali (sl. 1.18). S tako dobivenim
vektorima razapnemo ravninu. Treći vektor
projiciramo ortogonalno na tu ravninu, i odbijemo projekciju od njega.
Time smo dobili vektor okomit na ravninu (sl. 1.19), itd.
Slika 1.18:
Gram-Schmidtov postupak ortogonalizacije u ravnini.
Slika 1.19:
Gram-Schmidtov postupak ortogonalizacije u prostoru.
Ako međusobno okomite vlastite vektore normiramo (podijelimo s
njihovom duljinom), onda matrica
![$ X=[x_{ij}],$](img718.gif) čiji su stupci vektori
čiji su stupci vektori
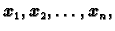 postaje ortogonalna. U tom slučaju je
postaje ortogonalna. U tom slučaju je
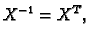 pa je
pa je
Hamilton-Cayleyev teorem za simetrične matrice.
Dijagonalizacija simetrične matrice nam omogućava da teorem
8 dokažemo za simetrične matrice elegantno.
Uočimo najprije da je
Odatle
Indukcijom se može dokazati da
općenito vrijedi
![% latex2html id marker 32232
$\displaystyle A^k=
X\,\left[\begin{array}{cccc}
...
...& \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\,X^{-1},$](img724.gif)
za
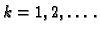
Prema tome i za proizvoljni polinom 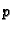 vrijedi
Neka je sada
vrijedi
Neka je sada 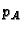 karakteristični
polinom matrice
karakteristični
polinom matrice 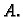 Budući da su
Budući da su
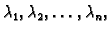 vlastite vrijednosti matrice
vlastite vrijednosti matrice 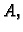 slijedi
slijedi
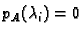 za svaki
za svaki 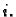 U tom slučaju je dijagonalna matrica na desnoj
strani nulmatrica, pa je
U tom slučaju je dijagonalna matrica na desnoj
strani nulmatrica, pa je
Ortogonalne matrice
Pogledajmo kako djeluje ortogonalna matrica 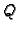 na prostoru
na prostoru
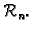 Iz
Iz
slijedi da 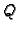 čuva skalarni produkt. Ako
stavimo
čuva skalarni produkt. Ako
stavimo
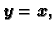 dobivamo
odakle
tj. ortogonalna matrica čuva duljinu vektora. Također
pa prema tome ortogonalna matrica čuva i kuteve do na predznak, jer
je kosinus kao parna funkcija neosjetljiv na predznak.
dobivamo
odakle
tj. ortogonalna matrica čuva duljinu vektora. Također
pa prema tome ortogonalna matrica čuva i kuteve do na predznak, jer
je kosinus kao parna funkcija neosjetljiv na predznak.
Budući da je 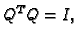 ortogonalna matrica je regularna i
ortogonalna matrica je regularna i
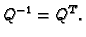 Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Prema tome je
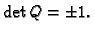
Vlastite vrijednosti i vlastiti vektori
ortogonalnih matrica
Neka je 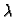 vlastita vrijednost, a
vlastita vrijednost, a
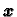 pripadni vlastiti vektor
ortogonalne matrice
pripadni vlastiti vektor
ortogonalne matrice 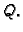 Tada je
Tada je
Konjugirajmo ovu
jednakost
Zbog svojstva
ortogonalnih matrica,
Budući da je
slijedi
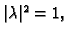 tj. kompleksan
broj
tj. kompleksan
broj 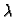 se nalazi na jediničnoj kružnici u Gaussovoj
ravnini. Specijalno, ako je
se nalazi na jediničnoj kružnici u Gaussovoj
ravnini. Specijalno, ako je 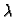 realan broj, onda je
realan broj, onda je 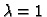 ili
ili
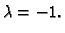
Pogledajmo sada što se može reći o ortogonalnim matricama drugog i
trećeg reda i o preslikavanjima koja one predstavljaju.
Ortogonalne matrice drugog reda
Ortogonalne matrice drugog reda možemo shvatiti kao funkcije (linearne
operatore) koje preslikavaju
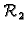 u
u
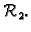 Neka je
Neka je
proizvoljna ortogonalna matrica drugog reda. Ona preslikava kanonsku
bazu u svoje stupce.
Prema tome stupci su međusobno okomiti, i njihova duljina jednaka je
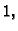 pa se pripadne točke nalaze na jediničnoj kružnici.
pa se pripadne točke nalaze na jediničnoj kružnici.
Uočimo prvi od njih. Prema upravo rečenom, postoji
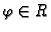 takav da je
takav da je
Slika 1.20:
Djelovanje ortogonalne matrice u ravnini.
Budući da je drugi stupac okomit na prvi, pripadna točka se nalazi
na jediničnoj kružnici na pravcu okomitom na radijvektor koji
pripada prvom stupcu. Takvih točaka imamo dvije, kao što se vidi na
sl. 1.20.
1. slučaj.
Radijvektor koji pripada točki zatvara kut
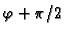 prema
pozitivnom dijelu osi
prema
pozitivnom dijelu osi 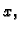 i prema tome
i prema tome
Tako imamo matricu
koja predstavlja rotaciju u ravnini oko
ishodišta za kut 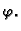
U ovom slučaju je očito 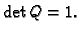
Nadalje
To je kvadratna jednadžba koja nema realnih rješenja, osim u
slučajevima kad je 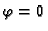 ili
ili
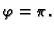 U tim slučajevima
rotacija je identično preslikavanje ili simetrija u odnosu na
ishodište. Dakle, možemo zaključiti da rotacija u ravnini za kut
U tim slučajevima
rotacija je identično preslikavanje ili simetrija u odnosu na
ishodište. Dakle, možemo zaključiti da rotacija u ravnini za kut
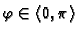 nema realnih vlastitih vektora, što je
geometrijski jasno.
nema realnih vlastitih vektora, što je
geometrijski jasno.
2. slučaj.
Radijvektor koji pripada točki zatvara kut
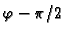 s
pozitivnim dijelom osi
s
pozitivnim dijelom osi 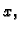 pa imamo
pa imamo
Matrica je sada
simetrična je, pa se može
dijagonalizirati. Karakteristična jednadžba je
Vlastite vrijednosti su
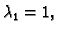
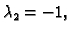 a vlastiti vektori su
Ako formiramo matricu
a vlastiti vektori su
Ako formiramo matricu 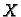 od ovih vektora, onda
je
U ovom slučaju se radi o simetriji u ravnini u odnosu na pravac čiji je
koeficijent smjera
od ovih vektora, onda
je
U ovom slučaju se radi o simetriji u ravnini u odnosu na pravac čiji je
koeficijent smjera
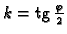 (sl. 1.21).
(sl. 1.21).
Slika 1.21:
Simetrija u ravnini.
U ovom slučaju je očito
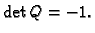
Zaključak.
Ortogonalne matrice drugog reda se dijele u dvije klase. U jednoj su
one čija je determinanta jednaka 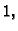 i one predstavljaju rotacije u
ravnini oko ishodišta. U drugoj su one čija je determinanta jednaka
i one predstavljaju rotacije u
ravnini oko ishodišta. U drugoj su one čija je determinanta jednaka
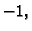 one su simetrične, i predstavljaju simetrije oko pravaca kroz
ishodište.
one su simetrične, i predstavljaju simetrije oko pravaca kroz
ishodište.
Ortogonalne matrice trećeg reda
Ortogonalne matrice trećeg reda možemo shvatiti kao funkcije koje
preslikavaju
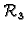 u
u
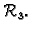 Vektor
Vektor
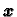 u
u
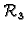 možemo
identificirati s uređenom trojkom realnih brojeva, dakle točkom u
prostoru, a prema tome i s radijvektorom u prostoru.
možemo
identificirati s uređenom trojkom realnih brojeva, dakle točkom u
prostoru, a prema tome i s radijvektorom u prostoru.
Neka je 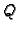 ortogonalna matrica trećeg reda. Njezin karakteristični
polinom je polinom trećeg reda s realnim koeficijentima, pa ima
točno jedan ili točno tri realna korijena (kompleksni korijeni u
tom slučaju dolaze u konjugiranim parovima). Realni korijeni mogu
biti samo
ortogonalna matrica trećeg reda. Njezin karakteristični
polinom je polinom trećeg reda s realnim koeficijentima, pa ima
točno jedan ili točno tri realna korijena (kompleksni korijeni u
tom slučaju dolaze u konjugiranim parovima). Realni korijeni mogu
biti samo 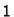 ili
ili 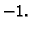
1. slučaj.
Ako su sva tri korijena realni, onda se može
pokazati da je matrica simetrična, i tada se ona može
dijagonalizirati, pa dobivamo jedan od sljedećih oblika
Te matrice predstavljaju redom identitet, simetriju u odnosu na
ravninu kroz ishodište (sl. 1.22), simetriju u odnosu na
pravac kroz ishodište (sl. 1.23), simetriju u odnosu
ishodište (sl. 1.24).
Slika 1.22:
Simetrija u odnosu na ravninu.
Slika 1.23:
Simetrija u odnosu na pravac.
Slika 1.24:
Simetrija u odnosu na ishodište.
2. slučaj.
Ako je samo jedna realna vlastita vrijednost, onda postoji vektor
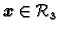 takav da je
takav da je
Neka je
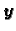 okomit na
okomit na
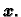 Tada
pa se
vidi da matrica
Tada
pa se
vidi da matrica 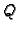 preslikava vektore koji su okomiti na
preslikava vektore koji su okomiti na
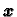 u vektore koji su i dalje okomiti na
u vektore koji su i dalje okomiti na
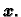 To znači da točke u ravnini kroz ishodište
okomitoj na pravac kroz radijvektor pridružen vektoru
To znači da točke u ravnini kroz ishodište
okomitoj na pravac kroz radijvektor pridružen vektoru
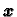 ostaju nakon preslikavanja u toj ravnini.
Preslikavanje u toj ravnini se može opisati ortogonalnom matricom
drugog reda. Ta matrica nema realne vlastite vrijednosti, jer bi ih u
protivnom matrica
ostaju nakon preslikavanja u toj ravnini.
Preslikavanje u toj ravnini se može opisati ortogonalnom matricom
drugog reda. Ta matrica nema realne vlastite vrijednosti, jer bi ih u
protivnom matrica 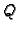 imala više od jedne. Tako ova matrica drugog
reda predstavlja rotaciju. Dakle, u ovom slučaju imamo ove tipove
Te matrice predstavljaju rotaciju u prostoru oko osi kroz ishodište
(sl. 1.25) i rotaciju u prostoru oko osi kroz ishodište
zajedno sa simetrijom u odnosu na ravninu rotacije (sl.
1.26).
imala više od jedne. Tako ova matrica drugog
reda predstavlja rotaciju. Dakle, u ovom slučaju imamo ove tipove
Te matrice predstavljaju rotaciju u prostoru oko osi kroz ishodište
(sl. 1.25) i rotaciju u prostoru oko osi kroz ishodište
zajedno sa simetrijom u odnosu na ravninu rotacije (sl.
1.26).
Slika 1.25:
Rotacija oko osi kroz ishodište.
Slika 1.26:
Simetrija u odnosu na ravninu i rotacija oko osi okomite
na tu ravninu.
Uočite da smo i u slučaju ortogonalnih matrica trećeg reda dobili
samo rotacije i simetrije.




Next: Sustavi običnih diferencijalnih jednadžbi
Up: Matrice i sustavi jednadžbi
Previous: Sustavi linearnih algebarskih jednadžbi
Contents
Index
Salih Suljagic
1999-12-17
![\begin{displaymath}
% latex2html id marker 31788
\left[
\begin{array}{cc}
2 & -1 \\ -1 & 2
\end{array}\right].\end{displaymath}](img598.gif) Uočite razliku između djelovanja na vektore
Uočite razliku između djelovanja na vektore
![]() i na ostale vektore. Slike vektora
i na ostale vektore. Slike vektora
![]() i
i
![]() su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
su ostale na pravcima
određenim s tim vektorima (original i slika su kolinearni), dok druge
vektore matrica zakreće.
![]() se može
drukčije napisati kao
se može
drukčije napisati kao
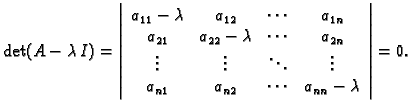
![]() -tog reda ima
-tog reda ima ![]() općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
općenito
kompleksnih rješenja, računajući njihovu kratnost. Ta rješenja su
vlastite vrijednosti.
![% latex2html id marker 31858
$\displaystyle A=\left[ \begin{array}{ccc}
3 & -2 & -4 \\
-1 & 1 & 1 \\
1 & -2 & -2
\end{array} \right].$](img616.gif)
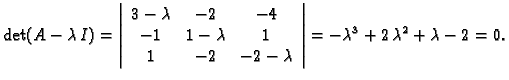
![]() pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
pripadni vlastiti vektor dobivamo (iz
(1.5)) kao rješenje sustava
![% latex2html id marker 31886
$\displaystyle \left[\begin{array}{c}
x_1 \\ -x_1 ...
...\end{array}\right]=x_1\left[\begin{array}{c}
1 \\ -1 \\ 1
\end{array}\right].$](img625.gif)
![% latex2html id marker 31908
$\displaystyle \left[\begin{array}{c}
x_1 \\ 0 \\ ...
...
\end{array}\right]=x_1\left[\begin{array}{c}
1 \\ 0 \\ 1
\end{array}\right].$](img631.gif)
![% latex2html id marker 31930
$\displaystyle \left[\begin{array}{c}
-2\,x_2 \\ x...
...end{array}\right]=x_2\left[\begin{array}{c}
-2 \\ 1 \\ -1
\end{array}\right].$](img636.gif)
![]() je simetrična,
ako je
je simetrična,
ako je ![]() tj. ako je
tj. ako je
![]() simetrična, onda vrijedi
simetrična, onda vrijedi
![]() simetrična matrica,
simetrična matrica, ![]() njezina vlastita vrijednost, i
njezina vlastita vrijednost, i
![]() pripadni vlastiti vektor. Tada je
pripadni vlastiti vektor. Tada je
![]() vlastita
vrijednost, i
vlastita
vrijednost, i
![]() njoj pripadni vlastiti vektor matrice
njoj pripadni vlastiti vektor matrice ![]() Također, neka je
Također, neka je ![]() vlastita vrijednost, i
vlastita vrijednost, i
![]() njoj pripadni
vlastiti vektor. Neka je
njoj pripadni
vlastiti vektor. Neka je
![]() Tada je
Tada je
![]() i
i
![]() Odatle
Odatle
![]()
![]()
![]() a kutevi u radijanima iznose
približno
a kutevi u radijanima iznose
približno ![]()
![]()
![]() odnosno
odnosno
![]()
![]()
![]()
![]() simetrična matrica, i neka su njezine vlastite
vrijednosti
simetrična matrica, i neka su njezine vlastite
vrijednosti
![]() međusobno
različite. Tada
međusobno
različite. Tada ![]() ima
ima ![]() međusobno okomitih vlastitih vektora
međusobno okomitih vlastitih vektora
![]() i
vrijedi
i
vrijedi
![% latex2html id marker 32065
$\displaystyle \boldsymbol{x}_j = [x_{ij}] = \left[...
... x_{2j} \\ \vdots \\ x_{nj}\end{array} \right],
\hspace{1cm}j=1,2,\ldots, n,$](img678.gif)
![% latex2html id marker 32071
$\displaystyle X = \left[\begin{array}{cccc} x_{11}...
...ots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nn}
\end{array}\right].$](img680.gif)
![% latex2html id marker 32085
$\displaystyle X^{-1}A\,X=[\lambda_j\,
\delta_{ij}]...
... & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n
\end{array}\right].$](img686.gif)
![% latex2html id marker 32089
$\displaystyle A=\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 2 & -1 \\
0 & -1 & 2
\end{array} \right].$](img687.gif)
![]()
![]() imamo vlastiti vektor
imamo vlastiti vektor
![% latex2html id marker 32095
$\displaystyle \left[\begin{array}{c}
0 \\ x_2 \\ ...
...\end{array}\right]=x_2\left[\begin{array}{c}
0 \\ 1 \\ -1
\end{array}\right],$](img690.gif)
![]() imamo (iz (1.5))
imamo (iz (1.5))
![% latex2html id marker 32121
$\displaystyle \left[\begin{array}{c}
1 \\ 0 \\ 0...
...ht], \quad \quad \quad \left[\begin{array}{c}
0 \\ 1 \\ 1
\end{array}\right].$](img696.gif)
![]() i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću
i također je povučen pravac
na kojem je svaki vektor vlastiti s vlastitom vrijednošću ![]()
![]() -struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću
-struka vlastita vrijednost
simetrične matrice vodi na sustav jednadžbi koji ima beskonačno
mnogo rješenja određenih pomoću ![]() parametara. Izborom ovih
parametara tako da jedan bude
parametara. Izborom ovih
parametara tako da jedan bude ![]() a ostali
a ostali ![]() dobivamo
dobivamo ![]() linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo
linearno
nezavisnih vektora. Ako tako napravimo za svaku višestruku vlastitu
vrijednost, i dodamo vlastite vektore koji pripadaju jednostrukim
vlastitim vrijednostima, dobit ćemo ![]() linearno nezavisnih vlastitih
vektora simetrične matrice
linearno nezavisnih vlastitih
vektora simetrične matrice ![]() Od njih kao stupaca formiramo matricu
Od njih kao stupaca formiramo matricu
![]() Ona je regularna, i vrijedi
Ona je regularna, i vrijedi
![]() može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice
može dijagonalizirati. U slučaju kad su
vlastite vrijednosti međusobno različite, dijagonalizacija se vrši
pomoću matrice čiji su stupci međusobno okomiti vlastiti
vektori matrice ![]()
![]() se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
se
može izabrati tako da su joj stupci međusobno okomiti. Doista, ako
su
![]() linearno nezavisni vlastiti vektori, onda su vektori
linearno nezavisni vlastiti vektori, onda su vektori
![]() dobiveni po formulama
dobiveni po formulama
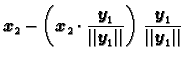
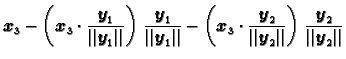
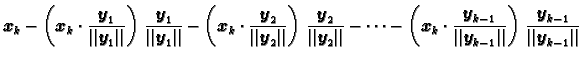
![]() čiji su stupci vektori
čiji su stupci vektori
![]() postaje ortogonalna. U tom slučaju je
postaje ortogonalna. U tom slučaju je
![]() pa je
pa je
![% latex2html id marker 32226
$\displaystyle A=X\,[\lambda_j\,
\delta_{ij}]\,X^{-...
...s & \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n
\end{array}\right]\,X^{-1}.$](img721.gif)
![% latex2html id marker 32228
$\displaystyle A^2=X\,\left[\begin{array}{cccc}
\la...
...s & \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n
\end{array}\right]\,X^{-1}=$](img722.gif)
![% latex2html id marker 32230
$\displaystyle = X\,\left[\begin{array}{cccc}
\lamb...
...& \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^2
\end{array}\right]\,X^{-1}.$](img723.gif)
![% latex2html id marker 32232
$\displaystyle A^k=
X\,\left[\begin{array}{cccc}
...
...& \ddots & \vdots \\
0 & 0 & \cdots & \lambda_n^k
\end{array}\right]\,X^{-1},$](img724.gif) za
za ![% latex2html id marker 32237
$\displaystyle p(A)=
X\,\left[\begin{array}{cccc}
...
... \ddots & \vdots \\
0 & 0 & \cdots & p(\lambda_n)
\end{array}\right]\,X^{-1}.$](img726.gif)
![]() na prostoru
na prostoru
![]() Iz
Iz
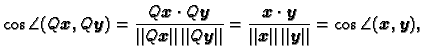
![]() ortogonalna matrica je regularna i
ortogonalna matrica je regularna i
![]() Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
Nadalje, iz svojstava determinante (Binet-Cauchyjevog
teorema) slijedi
![]() vlastita vrijednost, a
vlastita vrijednost, a
![]() pripadni vlastiti vektor
ortogonalne matrice
pripadni vlastiti vektor
ortogonalne matrice ![]() Tada je
Tada je
![]() u
u
![]() Neka je
Neka je
![% latex2html id marker 32314
$\displaystyle Q=\left[ \begin{array}{cc}
q_{11} & q_{12} \\
q_{21} & q_{22}
\end{array} \right]$](img751.gif)
![% latex2html id marker 32316
$\displaystyle \left[ \begin{array}{cc}
q_{11} & q_...
...nd{array} \right]=\left[ \begin{array}{c}
q_{12} \\ q_{22}
\end{array} \right]$](img752.gif)
![]() takav da je
takav da je
![]() prema
pozitivnom dijelu osi
prema
pozitivnom dijelu osi ![]() i prema tome
i prema tome
![% latex2html id marker 32335
$\displaystyle Q=
\left[ \begin{array}{cc}
\cos {\...
... & -\sin {\varphi } \\
\sin {\varphi } & \cos {\varphi }
\end{array} \right],$](img759.gif)
![]()
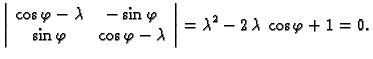
![]() s
pozitivnim dijelom osi
s
pozitivnim dijelom osi ![]() pa imamo
pa imamo
![% latex2html id marker 32356
$\displaystyle Q=
\left[ \begin{array}{cc}
\cos {\...
... & \sin {\varphi } \\
\sin {\varphi } & -\cos {\varphi }
\end{array} \right],$](img768.gif)
![% latex2html id marker 32364
$\displaystyle \left[ \begin{array}{c}
\cos\frac{\v...
...ray}{c}
-\sin\frac{\varphi }{2} \\ \cos\frac{\varphi }{2}
\end{array} \right].$](img772.gif)
![% latex2html id marker 32368
$\displaystyle X^{-1}Q\,X=\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]$](img773.gif)
![]()
![]() i one predstavljaju rotacije u
ravnini oko ishodišta. U drugoj su one čija je determinanta jednaka
i one predstavljaju rotacije u
ravnini oko ishodišta. U drugoj su one čija je determinanta jednaka
![]() one su simetrične, i predstavljaju simetrije oko pravaca kroz
ishodište.
one su simetrične, i predstavljaju simetrije oko pravaca kroz
ishodište.
![]() u
u
![]() Vektor
Vektor
![]() u
u
![]() možemo
identificirati s uređenom trojkom realnih brojeva, dakle točkom u
prostoru, a prema tome i s radijvektorom u prostoru.
možemo
identificirati s uređenom trojkom realnih brojeva, dakle točkom u
prostoru, a prema tome i s radijvektorom u prostoru.
![]() ortogonalna matrica trećeg reda. Njezin karakteristični
polinom je polinom trećeg reda s realnim koeficijentima, pa ima
točno jedan ili točno tri realna korijena (kompleksni korijeni u
tom slučaju dolaze u konjugiranim parovima). Realni korijeni mogu
biti samo
ortogonalna matrica trećeg reda. Njezin karakteristični
polinom je polinom trećeg reda s realnim koeficijentima, pa ima
točno jedan ili točno tri realna korijena (kompleksni korijeni u
tom slučaju dolaze u konjugiranim parovima). Realni korijeni mogu
biti samo ![]() ili
ili ![]()
![% latex2html id marker 32399
$\displaystyle \left[
\begin{array}{ccc}
1 & 0 & 0...
...n{array}{ccc}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1
\end{array} \right].$](img777.gif)
![]() takav da je
takav da je
![% latex2html id marker 32434
$\displaystyle \left[
\begin{array}{ccc}
1 & 0 & 0...
...sin {\varphi } \\
0 & \sin {\varphi } & \cos {\varphi }
\end{array} \right].$](img784.gif)