



Next: Rubni problemi
Up: Matrice i sustavi jednadžbi
Previous: Problem vlastitih ...
Contents
Index
Subsections
Primjer 1.26
Neka su dvije mase spojene oprugama za fiksnu točku kao na slici
1.27.
Slika 1.27:
Sustav od dva harmonijska oscilatora: a) ravnotežni položaj, b) u nekom trenutku 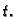
Ako zanemarimo otpor sredstva i težinu, onda za male oscilacije (u okviru
kojih vrijedi Hookeov zakon) imamo
Brojevi
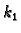
i
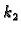
su pozitivni i oni karakteriziraju opruge.
Oscilacije ovog sistema će biti potpuno zadane ako definiramo u čas
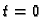
početne položaje i početne brzine:
Stavimo
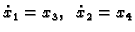
. Dobivamo sustav diferencijalnih
jednadžbi
uz početni uvjet
Osim što ovaj primjer pokazuje kako modeliranje konkretnog fizikalnog
problema dovodi do sustava diferencijalnih jednadžbi, on pokazuje također
kako se sustav u kojem se pojavljuju derivacije višeg reda može svesti na
sustav u kojem dolaze samo prve derivacije. Cijena za to je povećanje broja
jednadžbi, no to pokazuje da se možemo ograničiti na razmatranje sustava u
kojima dolaze samo prve derivacije.
Primjer 1.27
Dajmo jedan općenitiji primjer. Neka je fizikalni sustav
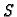
u
nekom vremenskom trenutku
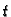
u potpunosti zadan s

veličina,
koje opisujemo kao funkcije vremena
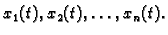
Pretpostavimo zatim da brzina promjene tih veličina ovisi
samo o njima samima. To se matematički izražava ovako
Ponašanje sustava
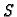
ovisi
još o stanju u kojem se nalazi u početnom trenutku. To zadajemo
početnim uvjetom za svaku veličinu
Posebno interesantne su one vrijednosti
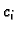
za koje je
Tada je
brzina promjene veličina
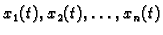
jednaka je nuli, pa se sustav
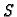
nalazi u ravnoteži. Pitanje je da li je ta ravnoteža stabilna. To
ispitujemo na taj način da sustav
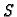
pomaknemo malo iz položaja
ravnoteže i ustanovimo što se događa. Stavimo
i uvrstimo u
diferencijalne jednadžbe
Uz
dodatni uvjet da funkcije
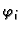
imaju neprekidne derivacije,
možemo primijeniti teorem srednje vrijednosti
gdje je
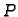
stanje sustava
između stanja
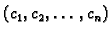
i
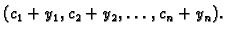
Budući da su pomaci iz
ravnotežnog stanja maleni, možemo umjesto
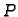
staviti
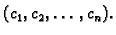
Tako imamo, uzimajući u obzir da je
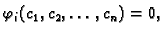
gdje je
Sustav običnih linearnih diferencijalnih jednadžbi 1. reda
Definicija 15
Sustav diferencijalnih jednadžbi oblika
gdje su
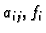
, za
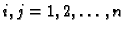
, neprekidne funkcije na
nekom intervalu
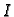
u
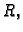
zovemo
sustavom
običnih linearnih diferencijalnih jednadžbi 1. reda.
Riješiti ovaj sustav znači naći funkcije
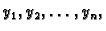 neprekidno derivabilne na intervalu
neprekidno derivabilne na intervalu 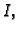 takve da
zadovoljavaju svaku od jednadžbi u sustavu. Uređena
takve da
zadovoljavaju svaku od jednadžbi u sustavu. Uređena  -torka
funkcija
-torka
funkcija
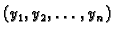 se zove rješenje.
se zove rješenje.
Cauchyev problem ili
problem početnog uvjeta jeste
problem da se za dani 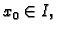 i proizvoljne brojeve
i proizvoljne brojeve
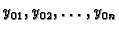 nađe rješenje sustava tako da vrijedi
nađe rješenje sustava tako da vrijedi
Ako stavimo
onda se sustav može zapisati kao
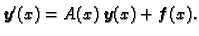 |
(1.7) |
Također Cauchyev problem možemo pisati u obliku
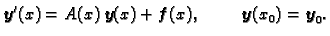 |
(1.8) |
Teorem 11
Neka su
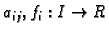
neprekidne funkcije na
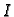
za
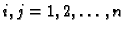
. Neka je
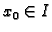
i
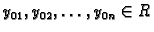
. Tada Cauchyev problem
ima jedno i samo jedno rješenje.
Dokaz.
Sustavi s konstantnim koeficijentima
Elementi matrice 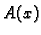 , funkcije
, funkcije 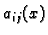 se zovu
koeficijenti. Ako su
koeficijenti konstantni, onda su elementi matrice
se zovu
koeficijenti. Ako su
koeficijenti konstantni, onda su elementi matrice  brojevi, pa
imamo sustav
brojevi, pa
imamo sustav
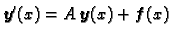 |
(1.9) |
uz početni uvjet
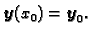 |
(1.10) |
Ovaj sustav se zove sustav linearnih
diferencijalnih jednadžbi 1. reda s konstantnim koeficijentima.
Ako je
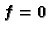 , tj. ako je
, tj. ako je
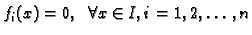 , onda se sustav zove homogen, u protivnom
sustav se zove nehomogen.
, onda se sustav zove homogen, u protivnom
sustav se zove nehomogen.
Primjer 1.28
Sustavi u primjerima
1.26 i
1.27 sustavi
su homogeni s konstantnim koeficijentima. Pri tom u primjeru
1.26 imamo Cauchyjev problem, koji se matrično može
zapisati na sljedeći način.
gdje je
Kod sustava u primjeru 1.27 je matrica sustava
gdje je radi kratkoće stavljeno
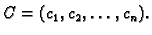
Označimo s 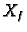 skup svih rješenja nehomogenog sustava, a s
skup svih rješenja nehomogenog sustava, a s 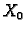 pripadnog homogenog sustava.
pripadnog homogenog sustava.
Teorem 12
Neka je
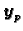
prozvoljno (partikularno) rješenje nehomogenog sustava.
Tada je
gdje
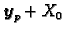
označava skup
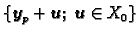
.
Dokaz. 1. Neka
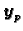 rješava
nehomogeni sustav, a
rješava
nehomogeni sustav, a
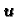 pripadni homogeni sustav
pripadni homogeni sustav
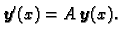 |
(1.11) |
To znači
Odatle
pa prema tome
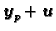 rješava nehomogeni sustav. To znači da je
rješava nehomogeni sustav. To znači da je
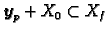 .
.
2. Neka je
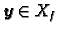 , tj neka vrijedi
Budući da je također
, tj neka vrijedi
Budući da je također
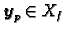 , slijedi
dakle
, slijedi
dakle
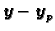 rješava pripadni homogeni sustav. Tako
postoji
rješava pripadni homogeni sustav. Tako
postoji
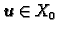 takav da je
tj.
Prema tome
takav da je
tj.
Prema tome
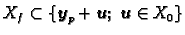 . Iz 1. i 2.
slijedi
. Iz 1. i 2.
slijedi
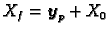 .
.
Na temelju ovog i prethodnog teorema zaključujemo da je
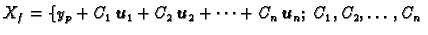
proizvoljne konstante
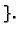
Dakle, da se nađe skup svih rješenja nehomogenog sustava, potrebno je
naći bazu prostora 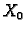 , tj.
, tj.  linearno nezavisnih rješenja
pripadnog homogenog i jedno rješenje nehomogenog sustava.
linearno nezavisnih rješenja
pripadnog homogenog i jedno rješenje nehomogenog sustava.
Metode rješavanja
Ovdje ćemo upoznati neke metode rješavanja sustava linearnih
diferencijalnih jednadžbi prvog reda s konstantnim koeficijentima
i pripadnog Cauchyjevog problema
Svođenje na jednu jednadžbu višeg
reda
Jedna od metoda se sastoji u tome da se višestrukim deriviranjem
jednadžbi izbace sve nepoznate funkcije osim jedne. Na taj način dolazimo
do jedne linearne diferencijalne jednadžbe  -tog reda, koju zatim
rješavamo poznatim metodama.
-tog reda, koju zatim
rješavamo poznatim metodama.
Primjer 1.29
Treba naći opće rješenje sustava
Rješenje.
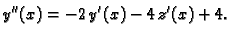 |
(1.13) |
Iz prve jednadžbe izračunamo
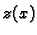
, uvrstimo u drugu i zatim
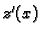
iz
druge uvrstimo u (
1.13). Dobivamo
Opće rješenje ove jednadžbe je
Uvrštavanjem u prvu jednadžbu možemo naći
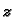
:
Dakle
pa vidimo da je
Specijalno, ako je početni uvjet
uvrštavanjem u opće rješenje dobivamo
i prema tome rješenje je
To rješenje vidimo na sljedećoj slici
Slika 1.28:
Rješenje sustava diferencijalnih jednadžbi, uz zadani početni uvjet.
Eulerova metoda
Druga metoda, Eulerova, se sastoji u tome da se rješenje pripadnog
homogenog sustava pretpostavi u obliku
gdje je
Uvrštavanje u (1.11) daje
pa dolazimo do poznatog problema da za matricu  nađemo vlastite
vrijednosti i vlastite vektore. Taj problem smo rješavali za simetrične i
ortogonalne matrice. Sada međutim matrica može biti proizvoljna. Problem
egzistencije i nalaženja vlastitih vrijednosti i vlastitih vektora za
proizvoljnu matricu nije tako jednostavan, pa to otežava diskusiju.
nađemo vlastite
vrijednosti i vlastite vektore. Taj problem smo rješavali za simetrične i
ortogonalne matrice. Sada međutim matrica može biti proizvoljna. Problem
egzistencije i nalaženja vlastitih vrijednosti i vlastitih vektora za
proizvoljnu matricu nije tako jednostavan, pa to otežava diskusiju.
Primjer 1.30
Riješimo primjer
1.29 na ovaj način.
Rješenje. Najprije promatramo pripadni homogeni sustav
tj.
Uvrstimo
Dobivamo sustav jednadžbi
Ovo je homogen sustav i on ima netrivijalno rješenje ako i samo ako je
determinanta sustava jednaka nuli. To vodi na kvadratnu jednadžbu
Slijedi
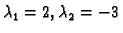
. Za
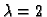
imamo
rješenje je
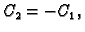
pa za
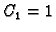
dobivamo vektor
Za
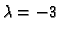
analogno
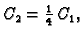
pa za
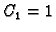
dobivamo
vektor
Rješenje homogenog sustava je tako
Partikularno rješenje dobivamo varijacijom konstanti
Uvrstimo ovo u (
1.12). Dobivamo sustav
Cramerovim pravilom nalazimo
Integracijom dobivamo
Dakle
što smo i trebali dobiti.
Ako sustav rješavamo Eulerovom metodom, onda se može dogoditi da neka
vlastita vrijednost od  ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
a) Vlastitoj vrijednosti je pridruženo onoliko linearno nezavisnih
vlastitih vektora kolika ja njena kratnost.
b) Vlastitoj vrijednosti pripada manje linearno nezavisnih vlastitih vektora
nego što je njena kratnost.
Pogledajmo na primjerima kako se ti problemi rješavaju.
Primjer 1.31
Treba naći opće rješenje sustava
Rješenje. Matrica sustava je
![% latex2html id marker 32943
$ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1
\end{array} \right]$](img953.gif) i prema tome očigledno je
i prema tome očigledno je
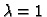 kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
gdje su
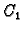
i
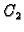
proizvoljne konstante.
Primjer 1.32
Treba naći opće rješenje sustava
Rješenje. Matrica sustava je
![% latex2html id marker 32956
$ \left[ \begin{array}{cc} 1 & 1 \\ 0 & 1
\end{array} \right],$](img958.gif) pa je
pa je
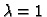 kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
odakle za
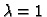
slijedi
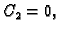
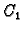
proizvoljan. Dakle vlastiti su
vektori oblika
![% latex2html id marker 32970
$ \; C_1 \left[ \begin{array}{c} 1 \\ 0 \end{array} \right].$](img962.gif)
Ti vektori čine jednodimenzionalan vektorski prostor, pa ne postoje dva
linearno nezavisna vektora. To je prema tome slučaj b). Riješimo taj
zadatak prvom metodom. Deriviranje prve jednadžbe dovodi do
pa je fundamentalni sustav rješenja
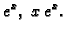
Tako je
Pomoću
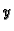
iz prve jednadžbe nađemo
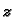
To možemo pisati u obliku
Primjer 1.33
Riješiti sustav
Rješenje. Ovaj sustav ima rješenja
tj.
Neki put se ne mogu lagano eliminirati sve nepoznate funkcije osim jedne kao
što se to radi u prvoj metodi. Pokušajte na primjer riješiti objema
metodama slijedeći primjer
U posljednjim primjerima smo rješavali homogene sustave radi
jednostavnosti. Da su bili nehomogeni, varijacijom konstanti dobili
bismo partikularno rješenje.
Dijagonalizacija matrice sustava
Sustav
možemo vrlo elegantno riješiti, ako se matrica  može
dijagonalizirati. Pretpostavimo da je to moguće, i da je
Da bismo dobili dijagonalnu
matricu pomnožimo jednadžbu s
može
dijagonalizirati. Pretpostavimo da je to moguće, i da je
Da bismo dobili dijagonalnu
matricu pomnožimo jednadžbu s 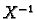 s lijeva.
gdje smo stavili
Ovaj sustav, kad se raspiše, svodi se na
s lijeva.
gdje smo stavili
Ovaj sustav, kad se raspiše, svodi se na  nezavisnih jednadžbi
Svaka od ovih jednadžbi je linearna diferencijalna jednadžba 1. reda,
čije rješenje je
Konstanta
nezavisnih jednadžbi
Svaka od ovih jednadžbi je linearna diferencijalna jednadžba 1. reda,
čije rješenje je
Konstanta 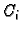 se izračuna iz početnog uvjeta, koji je sada
Kad tako dobijemo
se izračuna iz početnog uvjeta, koji je sada
Kad tako dobijemo
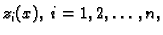 rješenje
rješenje
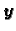 nađemo iz formule
nađemo iz formule
Ova metoda omogućava elegantno rješavanje, ako je matrica
simetrična. Neke nesimetrične matrice se također mogu
dijagonalizirati, kao što pokazuje primjer 1.24. Riješimo
sada metodom dijagonalizacije upravo jedan takav primjer sustava
diferencijalnih jednadžbi.
Primjer 1.34
Riješimo sljedeći sustav linearnih diferencijalnih jednadžbi 1. reda s konstantnim koeficijentima metodom dijagonalizacije.
Rješenje. Matrica sustava je
U primjeru
1.24 smo ustanovili da su vlastite vrijednosti
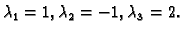
Vlastiti vektori su
Tako imamo
Zatim
Tako se sustav raspada na tri nezavisne linearne diferencijalne
jednadžbe 1. reda.
Svaku od njih riješimo, na pr. po formuli za rješenje linearne
diferencijalne jednadžbe 1. reda. Rješenje je
Da dobijemo rješenje zadanog sustava, trebamo naći
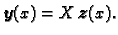
To znači
tj.
Na sljedećoj slici su dani grafovi rješenja uz zadani početni uvjet
koje je
Slika 1.29:
Rješenje sustava uz navedeni početni uvjet.
No postoje matrice koje se ne mogu dijagonalizirati. Najjednostavniji
oblik na koji se proizvoljna matrica može svesti je Jordanova
forma. U slučaju međusobno različitih vlastitih vrijednosti
Jordanova forma je dijagonalna matrica s vlastitim vrijednostima na
glavnoj dijagonali, dok u slučaju višestrukih vlastitih vrijednosti,
na pr. trostruke vlastite vrijednosti 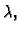 Jordanova forma
matrice trećeg reda je jedna od sljedeće tri matrice
Jordanova forma
matrice trećeg reda je jedna od sljedeće tri matrice
Detaljnije o Jordanovoj formi u [4].




Next: Rubni problemi
Up: Matrice i sustavi jednadžbi
Previous: Problem vlastitih ...
Contents
Index
Salih Suljagic
1999-12-17
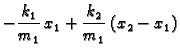
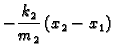
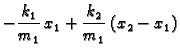
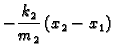
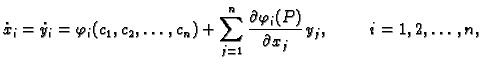
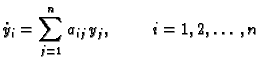
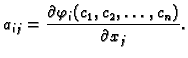
![]() neprekidno derivabilne na intervalu
neprekidno derivabilne na intervalu ![]() takve da
zadovoljavaju svaku od jednadžbi u sustavu. Uređena
takve da
zadovoljavaju svaku od jednadžbi u sustavu. Uređena ![]() -torka
funkcija
-torka
funkcija
![]() se zove rješenje.
se zove rješenje.
![]() i proizvoljne brojeve
i proizvoljne brojeve
![]() nađe rješenje sustava tako da vrijedi
nađe rješenje sustava tako da vrijedi
![\begin{displaymath}
% latex2html id marker 32595
\boldsymbol{y}=\left[
\begin{ar...
...c}
f_1(x) \\ f_2(x) \\ \vdots \\ f_n(x)
\end{array}\right],\end{displaymath}](img837.gif)
![\begin{displaymath}
% latex2html id marker 32597
A(x)=\left[
\begin{array}{cccc...
... a_{n1}(x) & a_{n2}(x) & \cdots & a_{nn}(x)
\end{array}\right],\end{displaymath}](img838.gif)
![]()
![]() , funkcije
, funkcije ![]() se zovu
koeficijenti. Ako su
koeficijenti konstantni, onda su elementi matrice
se zovu
koeficijenti. Ako su
koeficijenti konstantni, onda su elementi matrice ![]() brojevi, pa
imamo sustav
brojevi, pa
imamo sustav
![]() , tj. ako je
, tj. ako je
![]() , onda se sustav zove homogen, u protivnom
sustav se zove nehomogen.
, onda se sustav zove homogen, u protivnom
sustav se zove nehomogen.
![\begin{displaymath}
% latex2html id marker 32636
\boldsymbol{x}(t) = \left[\begi...
... \frac{k_2}{m_2} & -\frac{k_2}{m_2} & 0 & 0
\end{array}\right].\end{displaymath}](img852.gif)
![% latex2html id marker 32638
$\displaystyle A = \left[\begin{array}{cccc}
\frac{...
...l x_2} & \cdots & \frac{\partial\varphi_n(C)}{\partial x_n}
\end{array}\right],$](img853.gif)
![]() skup svih rješenja nehomogenog sustava, a s
skup svih rješenja nehomogenog sustava, a s ![]() pripadnog homogenog sustava.
pripadnog homogenog sustava.
![]() rješava
nehomogeni sustav, a
rješava
nehomogeni sustav, a
![]() pripadni homogeni sustav
pripadni homogeni sustav
![]() vektorski prostor. Neka su
vektorski prostor. Neka su
![]() dva rješenja
sustava (1.11) i
dva rješenja
sustava (1.11) i
![]() .
.
![\begin{displaymath}y_{01} \left[
\begin{array}{c}
1 \\
0 \\
\vdots \\
0
\end{...
...{c}
y_{01} \\
y_{02} \\
\vdots \\
y_{0n}
\end{array}\right].\end{displaymath}](img897.gif)
![\begin{displaymath}
% latex2html id marker 32798
C_1\,\boldsymbol{u}_1(x_0)+C_2\...
...y}{c}
C_1 \\
C_2 \\
\vdots \\
C_n
\end{array}\right].\end{displaymath}](img900.gif)
![]() -tog reda, koju zatim
rješavamo poznatim metodama.
-tog reda, koju zatim
rješavamo poznatim metodama.
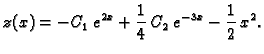
![\begin{displaymath}
% latex2html id marker 32847
\left[
\begin{array}{c}
y(x) \...
...gin{array}{c}
x+x^2 \\
-\frac{1}{2} x^2
\end{array}\right],\end{displaymath}](img917.gif)
![\begin{displaymath}
% latex2html id marker 32849
\boldsymbol{u}_1=e^{2x}\,\left[...
...ft[
\begin{array}{r}
1 \\
-\frac{1}{2}
\end{array}\right]. \end{displaymath}](img918.gif)
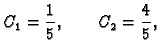
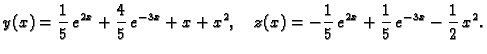
![% latex2html id marker 32864
$\displaystyle \boldsymbol{C}= \left[ \begin{array}{c} C_1 \\ C_2 \\ \vdots \\ C_n
\end{array} \right].$](img924.gif)
![\begin{displaymath}
% latex2html id marker 32877
\left[
\begin{array}{c}
y(x) \...
... \left[ \begin{array}{c}
y(x) \\
z(x)
\end{array} \right].\end{displaymath}](img929.gif)
![% latex2html id marker 32879
$\displaystyle \left[
\begin{array}{c}
y(x) \\
z(...
...right] = e^{\lambda x} \left[ \begin{array}{c}
C_1 \\
C_2
\end{array}\right].$](img930.gif)
![% latex2html id marker 32905
$\displaystyle \left[ \begin{array}{r} 1 \\ -1 \end{array}\right].$](img939.gif)
![% latex2html id marker 32913
$\displaystyle \left[ \begin{array}{r} 1 \\ \frac{1}{4} \end{array} \right]. $](img942.gif)
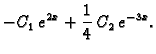
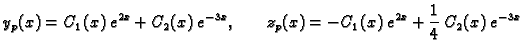
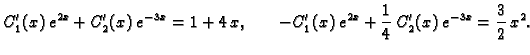
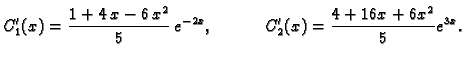
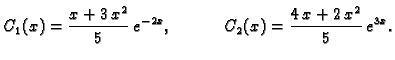

![]() ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
![% latex2html id marker 32943
$ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1
\end{array} \right]$](img953.gif) i prema tome očigledno je
i prema tome očigledno je
![]() kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
![\begin{displaymath}
% latex2html id marker 32947
\left[
\begin{array}{c} y \\ ...
...C_2\,e^x \left[
\begin{array}{c} 0 \\ 1 \end{array}
\right],\end{displaymath}](img954.gif)
![% latex2html id marker 32956
$ \left[ \begin{array}{cc} 1 & 1 \\ 0 & 1
\end{array} \right],$](img958.gif) pa je
pa je
![]() kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
![% latex2html id marker 32970
$ \; C_1 \left[ \begin{array}{c} 1 \\ 0 \end{array} \right].$](img962.gif) Ti vektori čine jednodimenzionalan vektorski prostor, pa ne postoje dva
linearno nezavisna vektora. To je prema tome slučaj b). Riješimo taj
zadatak prvom metodom. Deriviranje prve jednadžbe dovodi do
Ti vektori čine jednodimenzionalan vektorski prostor, pa ne postoje dva
linearno nezavisna vektora. To je prema tome slučaj b). Riješimo taj
zadatak prvom metodom. Deriviranje prve jednadžbe dovodi do
![% latex2html id marker 32988
$\displaystyle \left[ \begin{array}{c} y \\ z \end...
...{array} \right] +C_2\,e^x
\left[ \begin{array}{c} x \\ 1 \end{array} \right] .$](img970.gif)
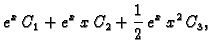
![% latex2html id marker 33029
$\displaystyle \boldsymbol{y}= C_1\,e^x \left[
\be...
...e^x \left[
\begin{array}{c}
\frac{1}{2}\,x^2 \\
x \\
1
\end{array}\right].$](img983.gif)
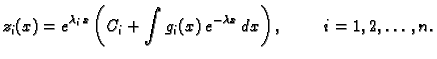
![% latex2html id marker 33105
$\displaystyle A=\left[ \begin{array}{ccc}
3 & -2 & -4 \\
-1 & 1 & 1 \\
1 & -2 & -2
\end{array} \right].$](img1005.gif)
![% latex2html id marker 33109
$\displaystyle \left[\begin{array}{c}
1 \\ -1 \\ ...
...array}\right],\quad
\left[\begin{array}{c}
-2 \\ 1 \\ -1
\end{array}\right].$](img1006.gif)
![% latex2html id marker 33111
$\displaystyle X = \left[\begin{array}{ccc}
1 & 1 &...
...}= \left[\begin{array}{c}
x\,\sin x \\ \cos 2\,x \\ x^2-1
\end{array}\right].$](img1007.gif)
![% latex2html id marker 33113
$\displaystyle X^{-1}\,A\,X = \left[\begin{array}{c...
...\,\sin x \\ -1 + x^2 + \cos 2\,x \\
-1 + x^2 - x\,\sin x \end{array}\right].$](img1008.gif)
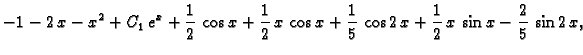
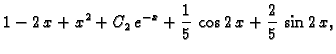
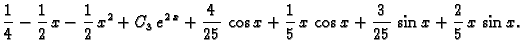
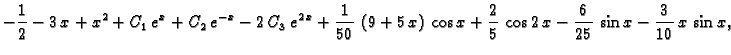
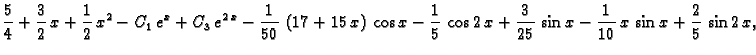
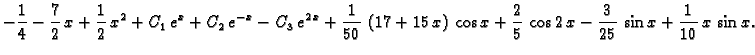
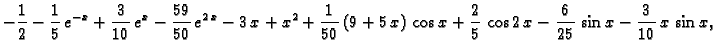
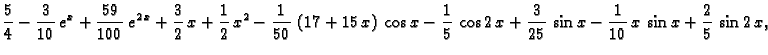
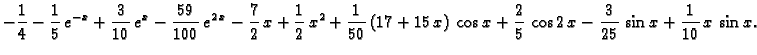
![]() Jordanova forma
matrice trećeg reda je jedna od sljedeće tri matrice
Jordanova forma
matrice trećeg reda je jedna od sljedeće tri matrice
![% latex2html id marker 33220
$\displaystyle \left[\begin{array}{ccc}
\lambda & 0...
...}
\lambda & 1 & 0 \\
0 & \lambda & 1 \\
0 & 0 & \lambda
\end{array}\right].$](img1034.gif)