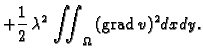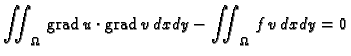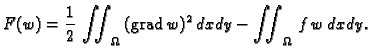



Next: Numerička matematika
Up: Rubni problemi
Previous: Varijacijske metode
Contents
Index
Subsections
Višedimenzionalni problemi
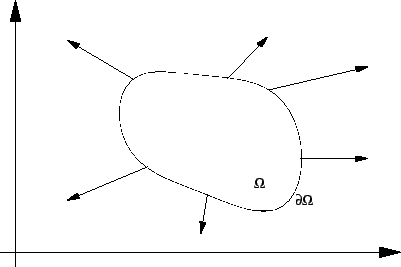
Rubni problemi
Oscilacije membrane
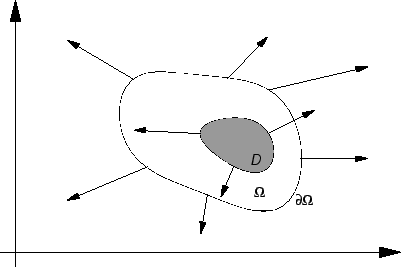
Membrana je tanka ploča od krutog materijala. Promatrat ćemo
nategnutu membranu silama koje djeluju u ravnini membrane.
Sila
djeluje na luk krivulje koja je rub membrane. Zbog krutosti membrane
napetost uslijed te sile prenosi se u unutrašnjost, pa tako na svaki
komad membrane 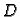 djeluje napetost na rubu
djeluje napetost na rubu
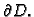 Tako, u
svakoj točki
Tako, u
svakoj točki 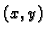 membrane, i za svaki luk kroz točku
membrane, i za svaki luk kroz točku 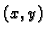 imamo silu
imamo silu
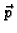 po jedinici duljine luka (linijsku gustoću
sile), kojom vanjski dio membrane djeluje na unutarnji dio. Ako luk
nije zatvoren, onda nije jasno što je vanjski, a što unutarnji
dio membrane. Pod vanjskim dijelom uvijek podrazumijevamo onaj dio
koji se nalazi na strani vektora normale. Sila o kojoj se ovdje radi
zove se kontaktna sila
(njezino djelovanje je omogućeno isključivo kontaktom). Zbog
pretpostavke da se radi o malim progibima, možemo pretpostaviti da
je ona, pa i njezina linijska gustoća, tangencijalna na
membranu. Pretpostavljamo, također, da napetost ne ovisi o
vremenu. Osnovna pretpostavka (Cauchyjev aksiom) je da je ta sila ista
za sve lukove kroz
po jedinici duljine luka (linijsku gustoću
sile), kojom vanjski dio membrane djeluje na unutarnji dio. Ako luk
nije zatvoren, onda nije jasno što je vanjski, a što unutarnji
dio membrane. Pod vanjskim dijelom uvijek podrazumijevamo onaj dio
koji se nalazi na strani vektora normale. Sila o kojoj se ovdje radi
zove se kontaktna sila
(njezino djelovanje je omogućeno isključivo kontaktom). Zbog
pretpostavke da se radi o malim progibima, možemo pretpostaviti da
je ona, pa i njezina linijska gustoća, tangencijalna na
membranu. Pretpostavljamo, također, da napetost ne ovisi o
vremenu. Osnovna pretpostavka (Cauchyjev aksiom) je da je ta sila ista
za sve lukove kroz 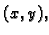 koji imaju zajednički
jedinični vektor normale
koji imaju zajednički
jedinični vektor normale 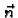 u točki
u točki 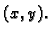 Tako
Tako
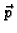 ovisi o točki i jediničnom vektoru normale u točki,
tj.
ovisi o točki i jediničnom vektoru normale u točki,
tj.
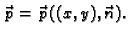 Ta ovisnost je
linearna, pa prema tome, ako je
onda vrijedi
Ta ovisnost je
linearna, pa prema tome, ako je
onda vrijedi
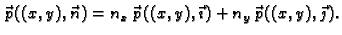 |
(2.45) |
Prema tome napetost 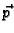 je određena svojim djelovanjem na
vektore
je određena svojim djelovanjem na
vektore
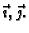 Neka je
Neka je
Time je napetost u točki 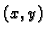 dana matricom
dana matricom
![% latex2html id marker 36141
$\displaystyle {\cal P}(x,y) = \left[ \begin{array}{cc} p_{11}(x,y) & p_{21}(x,y) \\ p_{12}(x,y) & p_{22}(x,y) \end{array}\right].$](img2001.gif) |
(2.48) |
Napetost u
smjeru vektora 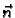 možemo izračunati tako da identificiramo
radijvektore s vektorstupcima, i da zatim vektorstupac
možemo izračunati tako da identificiramo
radijvektore s vektorstupcima, i da zatim vektorstupac
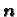 pomnožimo matricom
pomnožimo matricom 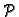 To isto se dobije, ako uvrstimo (2.46) i (2.47) u (2.45).
To isto se dobije, ako uvrstimo (2.46) i (2.47) u (2.45).
Pretpostavljamo da je membrana homogena i izotropno napeta, što ima za
posljedicu da napetost djeluje na rubu u smjeru vektora vanjske normale
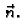
U tom slučaju je matrica napetosti skalarna
Tako je
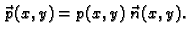
Ako je membrana u ravnoteži, onda ukupna sila na rubu iščezava.
Odatle
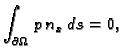
i
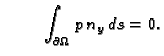
Budući da to vrijedi za svaki komad membrane 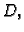 imamo
imamo
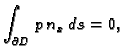 i i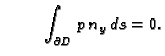 |
(2.49) |
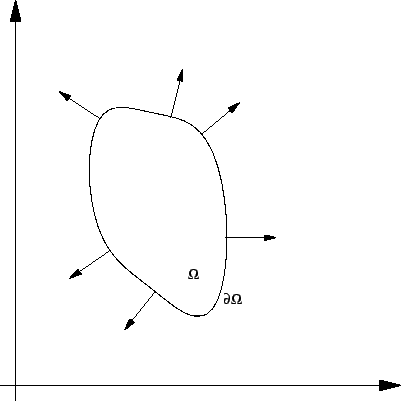
Teorem o divergenciji u 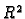 glasi
glasi
gdje je 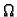 područje u ravnini,
područje u ravnini,
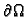 rub od
rub od
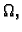 koji je po dijelovima glatka krivulja koja samu sebe ne
presijeca,
koji je po dijelovima glatka krivulja koja samu sebe ne
presijeca, 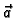 vektorsko polje klase
vektorsko polje klase 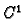 na nekoj okolini od
na nekoj okolini od
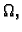 i
i 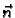 vektorsko polje vanjskih jediničnih normala
na
vektorsko polje vanjskih jediničnih normala
na
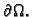
Specijalno, ako je
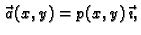 onda je
onda je
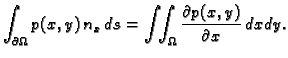 |
(2.50) |
Slično
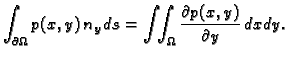 |
(2.51) |
Ove formule se zovu Gaussove formule.
Dakle, po teoremu o divergenciji, iz (2.49) slijedi
To vrijedi za proizvoljni komad membrane 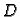 (područje u
(područje u 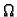 ), pa po
osnovnoj lemi zaključujemo da je
za svaki
), pa po
osnovnoj lemi zaključujemo da je
za svaki
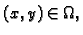 pa je prema tome
pa je prema tome
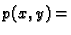
konst.
Osnovnim stanjem membrane smatrat ćemo ravnotežno stanje napete
membrane. Ako takvu membranu izvučemo iz položaja ravnoteže, ona se
počne gibati (oscilirati, titrati). Vektorska polja koja su nam pri
tom interesantna jesu
-
-
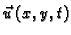 - progib membrane u točki
- progib membrane u točki 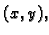 u čas
u čas
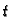 (polje pomaka),
(polje pomaka),
-
-
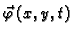 - količina gibanja membrane
po jedinici površine, u točki
- količina gibanja membrane
po jedinici površine, u točki 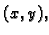 u čas
u čas 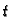 (površinska gustoća količine gibanja),
(površinska gustoća količine gibanja),
-
-
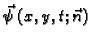 - količina gibanja, koja se u
jedinici vremena prenese kroz jedinični luk izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale
- količina gibanja, koja se u
jedinici vremena prenese kroz jedinični luk izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale 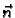 ) u
točki
) u
točki 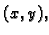 u čas
u čas 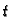 (linijska gustoća kontaktne sile),
(linijska gustoća kontaktne sile),
-
-
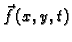 - količina gibanja po jedinici površine,
koja se u jedinici vremena izvana prenese na membranu u točki
- količina gibanja po jedinici površine,
koja se u jedinici vremena izvana prenese na membranu u točki
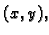 u čas
u čas 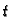 (površinska gustoća vanjske sile).
(površinska gustoća vanjske sile).
Polje
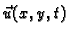 je kinematičko polje, a ostala tri polja su
dinamička.
je kinematičko polje, a ostala tri polja su
dinamička.
Zakon održanja.
Ukupna količina gibanja u jedinici vremena komada membrane 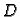 jednaka je ukupnoj
količini gibanja koja se po jedinici vremena izvana prenese na
membranu, kroz rub i drukčije.
jednaka je ukupnoj
količini gibanja koja se po jedinici vremena izvana prenese na
membranu, kroz rub i drukčije.
Promatrat ćemo samo male transverzalne oscilacije, pa je tako
Prvi zakon ponašanja kaže da je gustoća količine gibanja jednaka
umnošku gustoće mase i brzine
Drugi zakon ponašanja se izvodi slično kao kod žice.
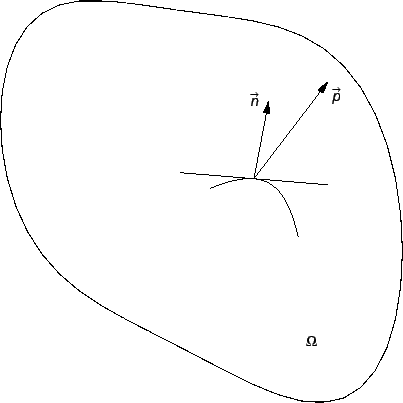
Vektorsko
polje
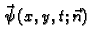 je tangencijalno na membranu i
okomito na luk
je tangencijalno na membranu i
okomito na luk 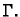 Nadalje je
Nadalje je
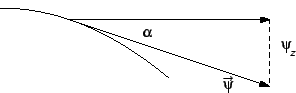
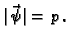 Slijedi (v. sliku)
Slijedi (v. sliku)
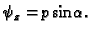 Progib membrane je malen, pa je kut
Progib membrane je malen, pa je kut 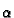 vrlo malen. Odatle
vrlo malen. Odatle
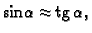 pa je
pa je
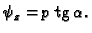 Zatim
Zatim
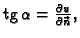 pa je
pa je
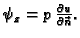 Uzdužna komponenta kontaktne sile je, zbog pretpostavke o
izotropnoj napetosti, uvijek okomita na rub, i po iznosu konstantna, pa nas
interesira samo
Uzdužna komponenta kontaktne sile je, zbog pretpostavke o
izotropnoj napetosti, uvijek okomita na rub, i po iznosu konstantna, pa nas
interesira samo 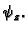 Također
ćemo pretpostaviti da vanjska sila djeluje samo u smjeru okomitom na
membranu, pa ćemo tako u daljnjem promatrati samo
Također
ćemo pretpostaviti da vanjska sila djeluje samo u smjeru okomitom na
membranu, pa ćemo tako u daljnjem promatrati samo
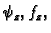 i te
veličine ćemo označavati s
i te
veličine ćemo označavati s 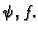 Imamo dakle drugi zakon ponašanja
Uvrstimo zakone ponašanja u zakon održanja i primijenimo Leibnizovo
pravilo o deriviranju pod znakom integrala. Dobivamo
Na prvi integral na desnoj strani primijenimo teorem o divergenciji,
pa imamo
Imamo dakle drugi zakon ponašanja
Uvrstimo zakone ponašanja u zakon održanja i primijenimo Leibnizovo
pravilo o deriviranju pod znakom integrala. Dobivamo
Na prvi integral na desnoj strani primijenimo teorem o divergenciji,
pa imamo
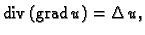 pa kad to uvrstimo, prebacimo sve na lijevu
stranu i stavimo pod jedan integral, dobivamo
Budući da ova jednakost vrijedi za svaki komad membrane
pa kad to uvrstimo, prebacimo sve na lijevu
stranu i stavimo pod jedan integral, dobivamo
Budući da ova jednakost vrijedi za svaki komad membrane 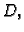 slijedi
tj.
Ova jednadžba se zove valna jednadžba. Ona opisuje male
poprečne oscilacije izotropno napete membrane.
slijedi
tj.
Ova jednadžba se zove valna jednadžba. Ona opisuje male
poprečne oscilacije izotropno napete membrane.
U slučaju da 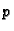 nije konstantno, dobili bismo jednadžbu
nije konstantno, dobili bismo jednadžbu
Provođenje topline
Promatrat ćemo provođenje topline kroz tijelo u prostoru. Slično
razmatranje se može provesti kad se radi o tankoj ploči u ravnini.
Polja koja u vezi s tim promatramo su sljedeća.
-
-
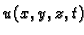 - temperatura tijela u točki
- temperatura tijela u točki 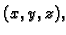 u čas
u čas 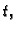
-
-
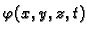 - količina topline po jedinici
volumena, u točki
- količina topline po jedinici
volumena, u točki 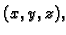 u čas
u čas 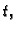
-
-
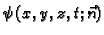 - količina topline, koja se u
jedinici vremena prenese kroz jediničnu površinu izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale
- količina topline, koja se u
jedinici vremena prenese kroz jediničnu površinu izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale 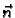 ) u
točki
) u
točki 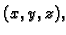 u čas
u čas 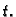
-
-
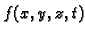 - količina topline po jedinici volumena, u
jedinici vremena, koja se izvana prenese u tijelo u točki
- količina topline po jedinici volumena, u
jedinici vremena, koja se izvana prenese u tijelo u točki
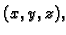 u čas
u čas 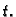
Polje
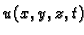 je kinematičko polje, a ostala tri polja su
dinamička.
je kinematičko polje, a ostala tri polja su
dinamička.
Zakoni ponašanja su
gdje je 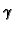 toplinski kapacitet jedinice volumena, a
toplinski kapacitet jedinice volumena, a 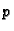 toplinski koeficijent
provođenja. Da bi se toplina prenosila izvana u tijelo, što znači
da je
toplinski koeficijent
provođenja. Da bi se toplina prenosila izvana u tijelo, što znači
da je 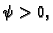 mora temperatura vani biti veća, tj. mora biti
mora temperatura vani biti veća, tj. mora biti
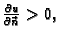 pa je prema tome
pa je prema tome 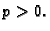
Kad provedemo sličan postupak kao za membranu, uzimajući sada zakon
o održanju energije kao polazište, dobivamo
jednadžbu provođenja topline
Filtracija
Promatrat ćemo filtraciju nestlačive tekućine kroz poroznu
sredinu. Polja koja su nam ovdje važna jesu
-
-
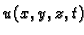 - tlak tekućine u točki
- tlak tekućine u točki 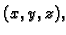 u čas
u čas 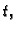
-
-
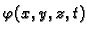 - masa tekućine po jedinici
volumena, u točki
- masa tekućine po jedinici
volumena, u točki 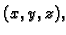 u čas
u čas 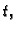
-
-
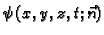 - masa tekućine, koja se u
jedinici vremena prenese kroz jediničnu površinu izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale
- masa tekućine, koja se u
jedinici vremena prenese kroz jediničnu površinu izvana prema unutra
(smjer suprotan smjeru jediničnog vektora vanjske normale 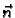 ) u
točki
) u
točki 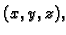 u čas
u čas 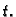
-
-
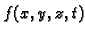 - masa tekućine po jedinici volumena, u
jedinici vremena, koja se unese u tijelo (izvori, ponori unutar
tijela) u točki
- masa tekućine po jedinici volumena, u
jedinici vremena, koja se unese u tijelo (izvori, ponori unutar
tijela) u točki 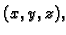 u čas
u čas 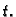
Polje
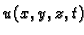 je kinematičko polje, a ostala tri polja su
dinamička.
je kinematičko polje, a ostala tri polja su
dinamička.
Zakoni ponašanja su
gdje je 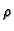 gustoća mase tekućine,
gustoća mase tekućine, 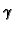 poroznost, tj. omjer praznog prostora i ukupnog volumena porozne sredine, a
poroznost, tj. omjer praznog prostora i ukupnog volumena porozne sredine, a 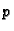 koeficijent filtracije. U ovom slučaju opću jednadžbu dobivamo iz
zakona o održanju mase. Kad uvrstimo zakone ponašanja dobivamo
jednadžbu filtracije
Za nestlačivu tekućinu
koeficijent filtracije. U ovom slučaju opću jednadžbu dobivamo iz
zakona o održanju mase. Kad uvrstimo zakone ponašanja dobivamo
jednadžbu filtracije
Za nestlačivu tekućinu 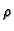 je
konstanta, pa bilo kakva derivacija od
je
konstanta, pa bilo kakva derivacija od 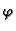 iščezava. Nadalje, prema Darcyjevom zakonu filtracije
(eksperimentalno utvrđenom) vrijedi
gdje je
iščezava. Nadalje, prema Darcyjevom zakonu filtracije
(eksperimentalno utvrđenom) vrijedi
gdje je 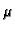 viskoznost tekućine, a
viskoznost tekućine, a 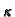 permeabilnost porozne
sredine. Pod pretpostavkom da su i ove veličine konstantne, dobivamo,
kao kod membrane, jednadžbu filtracije
Izostanak derivacije tlaka
permeabilnost porozne
sredine. Pod pretpostavkom da su i ove veličine konstantne, dobivamo,
kao kod membrane, jednadžbu filtracije
Izostanak derivacije tlaka  po vremenu tumačimo tako da se tlak u
nestlačivoj tekućini prenosi trenutno. Ovu jednadžbu možemo
prepisati u obliku
po vremenu tumačimo tako da se tlak u
nestlačivoj tekućini prenosi trenutno. Ovu jednadžbu možemo
prepisati u obliku
Jednadžba oblika
se zove Poissonova jednadžba, a jednadžba
Laplaceova jednadžba. Ravnotežna stanja membrane i
provođenja i filtracija nestlačive tekućine se opisuju Poissonovom
jednadžbom. Ako pri tom nije bilo vanjske sile, topline, mase, onda
se ta stanja opisuju Laplaceovom jednadžbom. Poissonova jednadžba je
linearna diferencijalna jednadžba, a Laplaceova je njoj pripadna
homogena jednadžba. Tako možemo zaključiti da se skup svih
rješenja Poissonove jednadžbe može dobiti tako da se jednom
partikularnom rješenju Poissonove jednadžbe dodaju sva moguća
rješenja Laplaceove jednadžbe. Funkcije koje rješavaju Laplaceovu
jednadžbu se zovu harmonijske funkcije. Kad se radi o
ravninskim problemima, onda se harmonijske funkcije pojavljuju kao
realni i imaginarni dijelovi analitičkih funkcija. To pokazuje da se
funkcije kompleksne varijable mogu koristiti kod ravninskih rubnih
problema ili onih prostornih koji se mogu svesti na ravninske.
Rubni problemi
Imamo tri tipa jednadžbi
-
-
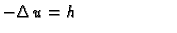 - ravnotežno stanje,
- ravnotežno stanje,
-
-
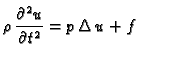 -
valna jednadžba,
-
valna jednadžba,
-
-
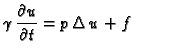 -
jednadžba provođenja.
-
jednadžba provođenja.
Rubni uvjeti mogu biti zadani tako da je na rubu
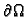 zadano kinematičko polje
zadano kinematičko polje 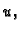 tj. da je zadana funkcija
tj. da je zadana funkcija
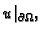 ili da je zadano dinamičko polje
ili da je zadano dinamičko polje 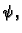 tj. da je zadana funkcija
tj. da je zadana funkcija
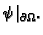 Iz zakona ponašanja
se vidi da zadati
Iz zakona ponašanja
se vidi da zadati 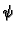 na rubu znači zapravo zadati funkciju
na rubu znači zapravo zadati funkciju
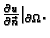 Napetost na
rubu je osnovna pretpostavka i ona ne ulazi u rubne uvjete.
Napetost na
rubu je osnovna pretpostavka i ona ne ulazi u rubne uvjete.
Kažemo da je zadan homogeni Dirichletov uvjet, ako je
Taj uvjet znači u slučaju
- a)
- oscilacija membrane, da je rub učvršćen u ravnini
membrane,
- b)
- provođenja topline, da se rub održava stalno na temperaturi
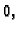
- c)
- filtracije, da je tlak na rubu jednak nuli, što znači da
tekućina može slobodno protjecati kroz rub.
Kažemo da je zadan homogeni Neumannov uvjet, ako je
Taj uvjet znači u slučaju
- a)
- oscilacija membrane, da ne ulazi (izlazi) nikakva količina
gibanja kroz rub; dakle rub nije izvana prisiljen ponašati se na
određen način, već se on ponaša onako kako mu diktira sama
membrana. Prema tome kažemo da je rub slobodan,
- b)
- provođenja topline, da kroz rub ne ulazi (izlazi) nikakva
toplina u tijelo; dakle rub je toplinski izoliran,
- c)
- filtracije, da kroz rub ne ulazi (izlazi) nikakva masa
tekućine u tijelo; dakle rub je nepropusan.
Ako proces nije stacionaran, onda je potrebno odrediti još i početne
uvjete. U slučaju valne jednadžbe treba zadati
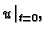
i
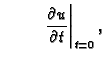
dok u slučaju jednadžbe provođenja dovoljno je zadati samo
Kao kod jednodimenzionalnih problema, koristeći svojstvo linearnosti
možemo homogenizirati rubne uvjete.
Jedinstvenost rješenja rubnih problema
Laplaceova jednadžba ima beskonačno mnogo rješenja. Dovoljno je
vidjeti da je funkcije oblika
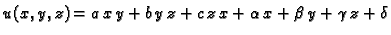 zadovoljavaju, za bilo
kakve vrijednosti parametara
zadovoljavaju, za bilo
kakve vrijednosti parametara
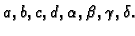 Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
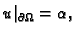
ili
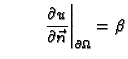
Taj problem ćemo rješavati pomoću energetske jednadžbe. Pomnožimo
Poissonovu jednadžbu s  i zatim integrirajmo po cijelom području
i zatim integrirajmo po cijelom području
Za skalarna polja  i
i 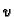 imamo
imamo
Stavimo 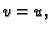 pa imamo
pa imamo
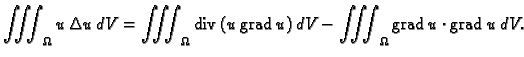 |
(2.52) |
Po teoremu o divergenciji
pa nakon uvrštavanja dobivamo energetsku jednadžbu
Teorem 19
Neka je
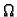
ograničeno područje u
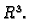
Dirichletov rubni problem
ima najviše jedno rješenje.
Dokaz. Zaista, pretpostavimo da su
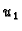 i
i 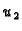 dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
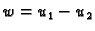 rješava rubni problem
rješava rubni problem
Uvrstimo 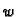 u energetsku jednadžbu umjesto
u energetsku jednadžbu umjesto 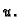 Imamo
Slijedi
odakle
pa je
Imamo
Slijedi
odakle
pa je 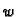 konstanta. No,
konstanta. No,
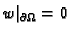 povlači
povlači 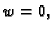 tj.
tj.
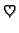
Teorem 20
Neka je
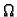
ograničeno područje u
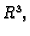
i neka je zadan
Neumannov rubni problem
- 1.
- Nužan uvjet za postojanje rješenja je
- 2.
- Bilo koja dva rješenja se razlikuju za konstantu.
Dokaz. 1. Ako je  rješenje, onda
iz jednadžbe slijedi
rješenje, onda
iz jednadžbe slijedi
Po teoremu o divergenciji slijedi
dakle
Ovaj uvjet izražava činjenicu da vanjska sila i Neumannov rubni
uvjet moraju biti pažljivo izabrani, tako da membrana bude u
ravnoteži. Kod Dirichletovog uvjeta nije bio potreban toliki oprez,
jer je u tom slučaju membrana na rubu učvršćena.
2. Neka su 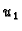 i
i
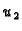 dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
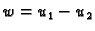 rješava rubni problem
Uvrstimo
rješava rubni problem
Uvrstimo 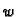 u energetsku jednadžbu umjesto
u energetsku jednadžbu umjesto 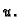 Imamo
Slijedi
odakle
pa je
Imamo
Slijedi
odakle
pa je 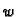 konstanta. Tako se
konstanta. Tako se 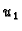 i
i 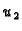 razlikuju za konstantu.
razlikuju za konstantu.
Metoda separacije varijabli (Fourierova metoda)
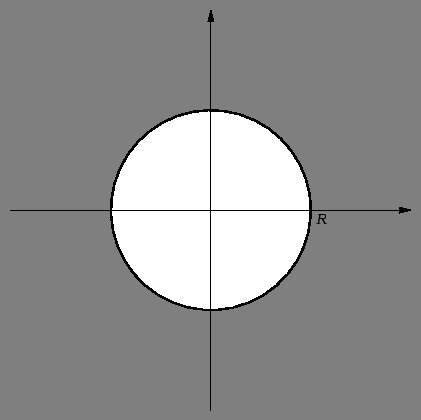
Dirichletov problem za ravnotežu kružne membrane
Dirichletov problem za ravnotežu kružne membrane glasi
gdje 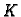 označava krug radiusa
označava krug radiusa 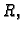 a
a
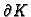 njegov rub,
kružnicu radiusa
njegov rub,
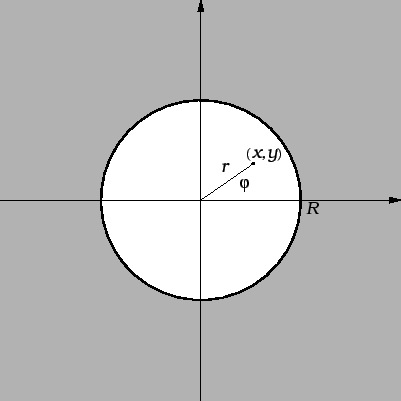
kružnicu radiusa 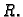 Prirodno je koordinatni sustav izabrati
sukladno geometrijskim karakteristikama područja. Zato u ovom
slučaju koristimo polarni koordinatni sustav u ravnini, i to tako da
ishodište stavimo u središte kruga.
Prirodno je koordinatni sustav izabrati
sukladno geometrijskim karakteristikama područja. Zato u ovom
slučaju koristimo polarni koordinatni sustav u ravnini, i to tako da
ishodište stavimo u središte kruga.
U polarnom koordinatnom sustavu su koordinate 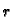 i
i 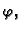
pa je
Postavlja se pitanje u što se transformira
kad se pređe na funkciju
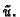 Po lančanom pravilu
Slično
Iz formula veze koordinatnih sustava slijedi
Kad to uvrstimo u
Po lančanom pravilu
Slično
Iz formula veze koordinatnih sustava slijedi
Kad to uvrstimo u
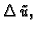 dobivamo
ili drukčije napisano
U daljnjem ćemo umjesto
dobivamo
ili drukčije napisano
U daljnjem ćemo umjesto 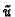 pisati radije
pisati radije 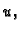 pa jednadžba
prema tome glasi
pa jednadžba
prema tome glasi
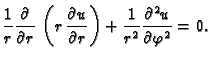 |
(2.53) |
Budući da smo ishodište polarnog koordinatnog sustava postavili u
središte kruga, čiji je radius 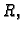 rubni uvjet se može zapisati
ovako
rubni uvjet se može zapisati
ovako
Rješenje tražimo u obliku
Uvrstimo u jednadžbu (2.53), dobivamo
Podijelimo s 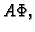 i pomnožimo s
i pomnožimo s 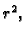 pa imamo
gdje je
pa imamo
gdje je 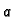 konstanta, jer smo separirali varijable. Imamo
Budući da je
konstanta, jer smo separirali varijable. Imamo
Budući da je 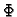 periodička funkcija (zbog geometrije problema),
periodička funkcija (zbog geometrije problema), 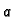 mora biti pozitivan, na pr.
mora biti pozitivan, na pr.
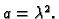 Slijedi
Opće rješenje druge jednadžbe je
Period funkcije
Slijedi
Opće rješenje druge jednadžbe je
Period funkcije 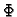 je
je 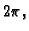 pa slijedi
Za drugu jednadžbu imamo dakle ova rješenja
Prva jednadžba sada glasi
pa slijedi
Za drugu jednadžbu imamo dakle ova rješenja
Prva jednadžba sada glasi
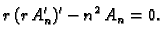 |
(2.54) |
Za 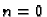 imamo
što nakon dijeljenja s
imamo
što nakon dijeljenja s 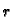 postaje
U slučaju
postaje
U slučaju 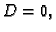 imamo
Ako je
imamo
Ako je 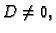 onda nakon još jednog dijeljenja s
onda nakon još jednog dijeljenja s 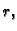 i
integriranja, dobivamo
pa je u tom slučaju opće rješenje
Rješenja za
i
integriranja, dobivamo
pa je u tom slučaju opće rješenje
Rješenja za 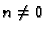 potražimo u obliku
Lako se vidi da je
Prema tome jednadžba (2.54) se svodi na
odakle
pa su tako rješenja jednadžbe (2.54) za
potražimo u obliku
Lako se vidi da je
Prema tome jednadžba (2.54) se svodi na
odakle
pa su tako rješenja jednadžbe (2.54) za 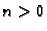 Opće rješenje za
Opće rješenje za 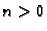 je
Budući da se radi o krugu, za koji je
je
Budući da se radi o krugu, za koji je
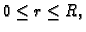 rješenja
rješenja 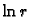 za
za 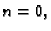 i
i
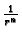 ne dolaze u obzir, jer te funkcije
teže u
ne dolaze u obzir, jer te funkcije
teže u 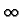 kad
kad
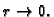 Tako imamo rješenja
Tako imamo rješenja
Sve ovo smo dobili direktno iz jednadžbe uz uvažavanje određenih
fizikalnih činjenica. Iskoristimo sada rubni uvjet. Nijedno od
rješenja 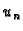 ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
što se može napisati ovako
Ovo rješenje mora zadovoljavati rubni uvjet
To je Fourierov red funkcije 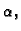 pa slijedi
pa slijedi
Sada moramo izbaciti rješenja 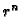 i
i 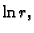 pa sličnim
rezoniranjem dolazimo do rješenja
gdje je, koristeći rubni uvjet,
pa sličnim
rezoniranjem dolazimo do rješenja
gdje je, koristeći rubni uvjet,
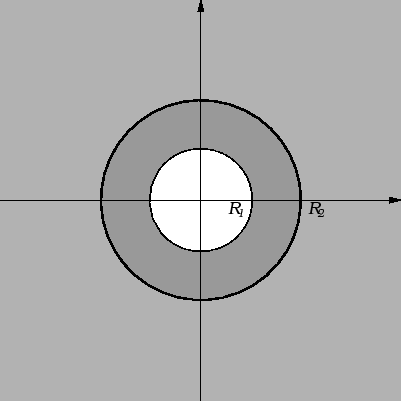
U tom slučaju imamo dva rubna uvjeta
gdje je 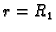 unutrašnji, a
unutrašnji, a 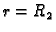 vanjski rub. Sada ne smijemo
izbaciti niti jedno partikularno rješenje, pa rješenje rubnog
problema pretpostavljamo u obliku
Za
vanjski rub. Sada ne smijemo
izbaciti niti jedno partikularno rješenje, pa rješenje rubnog
problema pretpostavljamo u obliku
Za 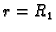 desnu stranu možemo shvatiti kao Fourierov red funkcije
desnu stranu možemo shvatiti kao Fourierov red funkcije
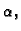 a za
a za 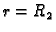 kao Fourierov red funkcije
kao Fourierov red funkcije 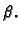 Tako imamo
za
Tako imamo
za
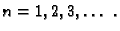 Za svaki
Za svaki 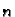 treba riješiti sustav od dvije
jednadžbe s dvije nepoznanice da bi se dobili neodređeni
koeficijenti u rješenju.
treba riješiti sustav od dvije
jednadžbe s dvije nepoznanice da bi se dobili neodređeni
koeficijenti u rješenju.
Primjer 2.22
Neka je dana beskonačna homogena kružna cijev, čiji je unutarnji
radius
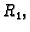
a vanjski
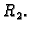
Unutarnja stijena cijevi se održava na
stalnoj temperaturi
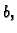
a vanjska na temperaturi
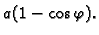
Naći raspodjelu temperature u tijelu
cijevi nakon što se uspostavi toplinska ravnoteža.
Rješenje. Beskonačnost cijevi nam, zajedno s homogenošću omogućuje da na
problem gledamo kao na dvodimenzionalni. U tom slučaju se, naime, u
svakom poprečnom presjeku uspostavi isto ravnotežno stanje. Problem
je prema tome ekvivalentan problemu toplinske ravnoteže unutar
prstena, tj. rubnom problemu
Rješenje će biti oblika
gdje je
Rješenja ovih sustava jednadžbi su
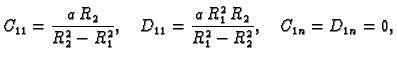
za
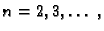
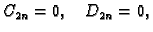
za
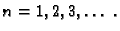
Prema tome rješenje je
Rubni problem za ravnotežu pravokutne membrane učvršćene na rubu
glasi
gdje je 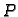 pravokutnik
pravokutnik
![$ [0,a]\times [0,b].$](img2211.gif)
Pretpostavimo da je 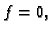 i da je
i da je
s tim da, zbog pretpostavke o neprekidnosti membrane, mora biti
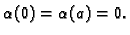
Pretpostavimo rješenje u obliku
Iz
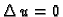 slijedi
gdje je
slijedi
gdje je 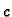 konstanta, jer smo separirali varijable. Odatle
Kao i u
2.3.3 zaključujemo da je
konstanta, jer smo separirali varijable. Odatle
Kao i u
2.3.3 zaključujemo da je 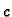 negativan, pa možemo pisati
negativan, pa možemo pisati
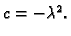
Tako imamo
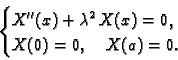 |
(2.55) |
Rješenja problema (2.55) jesu funkcije
Druga jednadžba
daje rješenja
Rješenje rubnog problema tražimo u obliku
Iz rubnog uvjeta 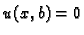 slijedi
pa je
Iz rubnog uvjeta
slijedi
pa je
Iz rubnog uvjeta
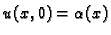 imamo
Odatle
imamo
Odatle
Ako je uvjet na rubu složeniji, onda se problem rastavlja na nekoliko
ovakvih.
Primjer 2.23
Naći ravnotežu pravokutne tanke ploče (membrane) uz sljedeće
uvjete na rubu
Rješenje. Treba riješiti problem
Objasnili smo kako se rješava rubni problem za ravnotežu
pravokutne membrane u slučaju kad je rubni uvjet homogen na tri od
četiri ruba. Ovaj problem ćemo riješiti tako da ga rastavimo na
nekoliko problema, od kojih je svaki problem tipa koji smo objasnili.
Prvi korak u tome je da pogodnom, jednostavnom supstitucijom osiguramo
da pomak membrane u vrhovima pravokutnika bude 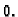 Stavimo
Stavimo
i odredimo
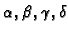
tako da je
Dobivamo sustav jednadžbi
Rješenje je
Prema tome početni problem smo sveli na sljedeći
Neka je 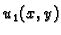 rješenje rubnog problema
rješenje rubnog problema
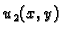
rješenje rubnog problema
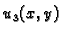
rješenje rubnog problema
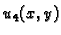
rješenje rubnog problema
Tada je očito
odnosno
Metoda separacije varijabli za nestacionarne probleme
Nestacionarni problemi su opisani valnom jednadžbom
ili jednadžbom provođenja
na nekom području 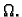 Ovdje smo radi jednostavnosti uzeli da
su gustoća mase
Ovdje smo radi jednostavnosti uzeli da
su gustoća mase 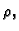 i specifična toplina
i specifična toplina 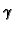 konstante. Također smo pretpostavili da nema vanjskog utjecaja, tj. da je
konstante. Također smo pretpostavili da nema vanjskog utjecaja, tj. da je 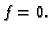
Pretpostavimo da je rubni uvjet Dirichletov
Početni uvjeti za valnu jednadžbu neka su
za
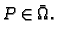 Ovdje
Ovdje
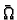 označava područje
označava područje
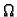 zajedno s rubom
zajedno s rubom
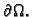
Osnovna pretpostavka je da se rješenje može predstaviti u obliku
produkta
Uvrstimo u jednadžbu, na pr. valnu
i podijelimo s
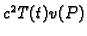 Budući da smo separirali varijable, i da su one nezavisne,
Budući da smo separirali varijable, i da su one nezavisne, 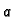 je konstanta.
Pomnožimo ovu jednadžbu s
je konstanta.
Pomnožimo ovu jednadžbu s 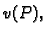 i integriramo po
i integriramo po 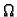 Imamo, zbog (2.52),
jer se
Imamo, zbog (2.52),
jer se 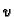 poništava na
poništava na
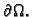 Tako je
Dakle možemo staviti
Tako je
Dakle možemo staviti
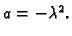 Tako se početna jednadžba
raspada na dvije jednadžbe
Rubni uvjet je sada
Tako se početna jednadžba
raspada na dvije jednadžbe
Rubni uvjet je sada
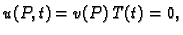
za
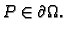
Kako to vrijedi za svaki 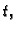 mora biti
mora biti 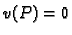 na
na
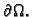 Tako imamo rubni problem
Oni
Tako imamo rubni problem
Oni
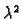 za koje postoji netrivijalno rješenje ovog problema
zovu se vlastite vrijednosti, a pripadne funkcije
vlastite funkcije ovog rubnog problema.
za koje postoji netrivijalno rješenje ovog problema
zovu se vlastite vrijednosti, a pripadne funkcije
vlastite funkcije ovog rubnog problema.
Neka su 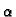 i
i 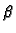 dvije međusobno različite vlastite
vrijednosti, i
dvije međusobno različite vlastite
vrijednosti, i 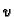 odnosno
odnosno 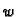 pripadne vlastite funkcije. Tada
pripadne vlastite funkcije. Tada
S druge strane, prema drugoj Greenovoj formuli, koja se izvodi iz (2.52),
jer je
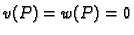 za
za
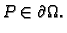 Tako je
Budući da je
Tako je
Budući da je
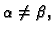 slijedi
Zbog ovog svojstva kažemo da su vlastite funkcije, koje pripadaju
različitim vlastitim vrijednostima, međusobno okomite. Opravdanje
leži u činjenici da produkt
koji paru funkcija pridružuje broj (skalar),
ima sva svojstva skalarnog produkta.
slijedi
Zbog ovog svojstva kažemo da su vlastite funkcije, koje pripadaju
različitim vlastitim vrijednostima, međusobno okomite. Opravdanje
leži u činjenici da produkt
koji paru funkcija pridružuje broj (skalar),
ima sva svojstva skalarnog produkta.
Pretpostavimo sada da su
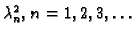 vlastite
vrijednosti, a
vlastite
vrijednosti, a
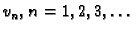 vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
Rješenja su
Rješenje cijelog rubno-početnog problema tražimo u obliku
Neodređene konstante
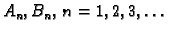 računamo iz
početnih uvjeta, pomoću Fourierovih redova.
računamo iz
početnih uvjeta, pomoću Fourierovih redova.
Kod jednadžbe provođenja jedina je razlika u vremenskoj
jednadžbi. Ona u tom slučaju glasi
pa je
Rješenje cijelog problema se tada traži u obliku
a neodređene konstante 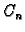 se određuju iz početnog uvjeta pomoću
Fourierovog reda.
se određuju iz početnog uvjeta pomoću
Fourierovog reda.
Varijacijski princip
Rješavamo rubni problem
Svaku funkciju 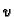 klase
klase
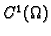 takvu da je
takvu da je
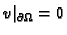 zovemo dopustivom funkcijom.
zovemo dopustivom funkcijom.
Pretpostavimo da je 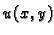 ravnotežni položaj membrane, tj. rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije
ravnotežni položaj membrane, tj. rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije 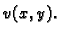 Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i
Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i 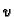 biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka
biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka 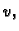 je
je
dok je unutrašnji rad membrane
Ako jednadžbu u (2.56) pomnožimo s 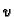 i integriramo po
i integriramo po
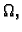 dobivamo
Ova jednakost
izražava Bernoullijev princip sačuvanja rada (energije). Iz prve
Greenove formule
slijedi
jer je
dobivamo
Ova jednakost
izražava Bernoullijev princip sačuvanja rada (energije). Iz prve
Greenove formule
slijedi
jer je 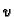 dopustiva funkcija, pa iščezava na rubu od
dopustiva funkcija, pa iščezava na rubu od 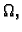 a
s njom i krivuljni integral. Kad to uvrstimo u gornju jednakost,
dobivamo
a
s njom i krivuljni integral. Kad to uvrstimo u gornju jednakost,
dobivamo
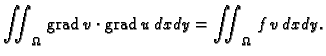 |
(2.57) |
Možemo zaključiti sljedeće. Ako funkcija  rješava rubni problem
(2.56), onda za svaku dopustivu funkciju
rješava rubni problem
(2.56), onda za svaku dopustivu funkciju 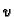 vrijedi
(2.57). Također vrijedi i obrat. Ako
vrijedi
(2.57). Također vrijedi i obrat. Ako  sa svojstvom
sa svojstvom
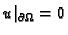 zadovoljava (2.57) za svaku
dopustivu funkciju
zadovoljava (2.57) za svaku
dopustivu funkciju 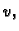 onda
onda  rješava rubni problem (2.56).
rješava rubni problem (2.56).
Prvi dio smo dokazali. Treba dokazati obrat.
Neka vrijedi (2.57) za svaku dopustivu funkciju 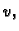 i neka
je
i neka
je
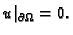 Tada je prema prvoj Greenovoj formuli
Tada je prema prvoj Greenovoj formuli
Krivuljni integral iščezava, jer je 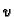 dopustiva funkcija. Tako je
Uvrstimo u (2.57), dobivamo
za svaku dopustivu funkciju
dopustiva funkcija. Tako je
Uvrstimo u (2.57), dobivamo
za svaku dopustivu funkciju 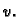 Po osnovnoj lemi slijedi
Po osnovnoj lemi slijedi
Kao i u jednodimenzionalnom slučaju sada dokazujemo da je
Bernoullijev princip ekvivalentan problemu minimizacije
funkcionala energije.
Neka je dan funkcional
Pogledajmo čime se odlikuje 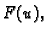 ako
ako  zadovoljava Bernoullijev
princip, tj. zadovoljava (2.57). U tu svrhu stavimo
zadovoljava Bernoullijev
princip, tj. zadovoljava (2.57). U tu svrhu stavimo
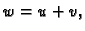 gdje je
gdje je 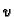 perturbacija
ravnotežnog položaja (dopustiva funkcija). Kako je
perturbacija
ravnotežnog položaja (dopustiva funkcija). Kako je  ravnotežni
položaj,
ravnotežni
položaj,  je dopustiva funkcija, pa je i
je dopustiva funkcija, pa je i 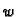 dopustiva. Imamo
Dakle
dopustiva. Imamo
Dakle
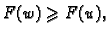 i pri tom je
i pri tom je 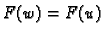 samo ako je
samo ako je
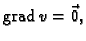 a to znači
a to znači
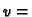 konst.
konst.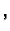 a kako je na rubu
a kako je na rubu
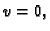 slijedi da je
slijedi da je 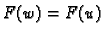 samo ako je
samo ako je 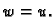 Dakle
Dakle  je
jedinstvena funkcija sa svojstvom
je
jedinstvena funkcija sa svojstvom
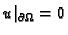 koja
minimizira funkcional
koja
minimizira funkcional 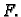
Dokažimo sada obrat, tj. da funkcija  koja minimizira funkcional
koja minimizira funkcional
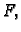 i zadovoljava rubni uvjet
i zadovoljava rubni uvjet
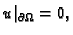 mora
zadovoljavati Bernoullijev princip, tj. (2.57). Pretpostavimo da
mora
zadovoljavati Bernoullijev princip, tj. (2.57). Pretpostavimo da  ima tražena svojstva, i
stavimo
ima tražena svojstva, i
stavimo
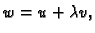 gdje je
gdje je 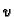 perturbacija (funkcija iz klase
dopustivih). Funkcional
perturbacija (funkcija iz klase
dopustivih). Funkcional 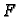 poprima minimum na funkciji
poprima minimum na funkciji 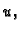 pa prema
tome funkcija
pa prema
tome funkcija
poprima minimum za
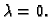 Imamo
Ovo je polinom drugog stupnja u
Imamo
Ovo je polinom drugog stupnja u
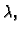 koeficijent uz
koeficijent uz
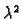 je pozitivan, pa funkcija doista ima minimum u
tjemenu. Apscisa tjemena parabole, koja je graf funkcije
je
pa ako se minimum dostiže u
je pozitivan, pa funkcija doista ima minimum u
tjemenu. Apscisa tjemena parabole, koja je graf funkcije
je
pa ako se minimum dostiže u
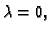 tj. u točki s apscisom
tj. u točki s apscisom
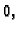 onda mora biti
onda mora biti 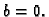 U našem slučaju slijedi
za svaku dopustivu funkciju
U našem slučaju slijedi
za svaku dopustivu funkciju 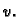 Tako smo dokazali da
Tako smo dokazali da  zadovoljava
(2.57). Iz svega rečenog možemo zaključiti da vrijedi sljedeće.
zadovoljava
(2.57). Iz svega rečenog možemo zaključiti da vrijedi sljedeće.
Teorem 21 (
Varijacijski princip)
Da bi funkcija

bila rješenje rubnog problema
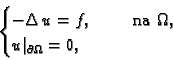 |
(2.58) |
nužno je i dovoljno da funkcija  zadovoljava taj rubni uvjet i da
minimizira funkcional
zadovoljava taj rubni uvjet i da
minimizira funkcional




Next: Numerička matematika
Up: Rubni problemi
Previous: Varijacijske metode
Contents
Index
Salih Suljagic
1999-12-17

![% latex2html id marker 36149
$\displaystyle \left[
\begin{array}{cc}
p_{11}(x,y)...
...+ p_{12}(x,y)\,n_y \\
p_{21}(x,y)\,n_x + p_{22}(x,y)\,n_y
\end{array}\right].$](img2005.gif)
![]()
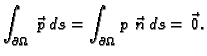
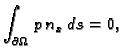 i
i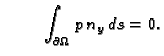
![]() glasi
glasi
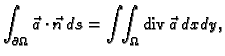
![]() onda je
onda je
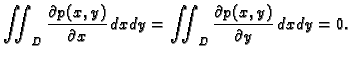
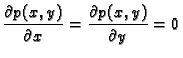
![]() jednaka je ukupnoj
količini gibanja koja se po jedinici vremena izvana prenese na
membranu, kroz rub i drukčije.
jednaka je ukupnoj
količini gibanja koja se po jedinici vremena izvana prenese na
membranu, kroz rub i drukčije.
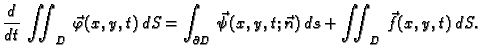
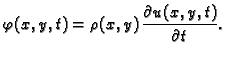

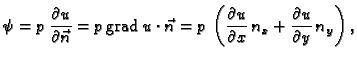
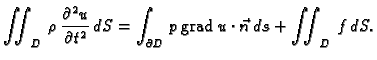
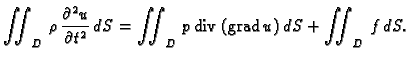
![$\displaystyle \iint_{D}\,\left[\rho\,\frac{\partial^2 u}{\partial t^2} - p\,\Delta\,u -
f\right]\,dS = 0.$](img2053.gif)
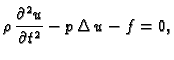
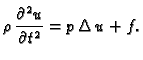
![]() nije konstantno, dobili bismo jednadžbu
nije konstantno, dobili bismo jednadžbu
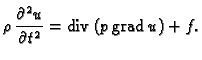
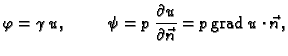
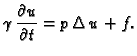
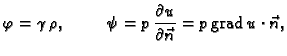
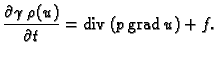
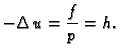
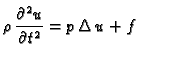 -
valna jednadžba,
-
valna jednadžba,
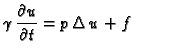 -
jednadžba provođenja.
-
jednadžba provođenja.
![]() zadano kinematičko polje
zadano kinematičko polje ![]() tj. da je zadana funkcija
tj. da je zadana funkcija
![]() ili da je zadano dinamičko polje
ili da je zadano dinamičko polje ![]() tj. da je zadana funkcija
tj. da je zadana funkcija
![]() Iz zakona ponašanja
se vidi da zadati
Iz zakona ponašanja
se vidi da zadati ![]() na rubu znači zapravo zadati funkciju
na rubu znači zapravo zadati funkciju
![]() Napetost na
rubu je osnovna pretpostavka i ona ne ulazi u rubne uvjete.
Napetost na
rubu je osnovna pretpostavka i ona ne ulazi u rubne uvjete.
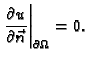
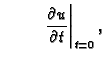
![]() zadovoljavaju, za bilo
kakve vrijednosti parametara
zadovoljavaju, za bilo
kakve vrijednosti parametara
![]() Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
Tako i Poissonova jednadžba ima beskonačno mnogo rješenja. Realna
fizikalna situacija je membrana određenog oblika, s određenim
uvjetima na rubu. To drastično smanjuje broj rješenja. Razmotrimo
sada problem jedinstvenosti rubnog problema
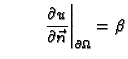
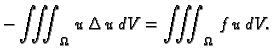
![]() i
i ![]() imamo
imamo
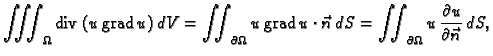
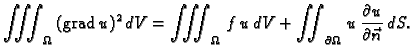
![]() i
i ![]() dva rješenja. Tada funkcija
dva rješenja. Tada funkcija
![]() rješava rubni problem
rješava rubni problem

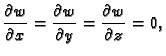
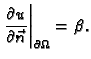
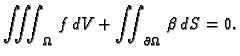
![]() rješenje, onda
iz jednadžbe slijedi
rješenje, onda
iz jednadžbe slijedi
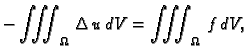
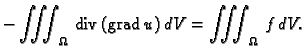
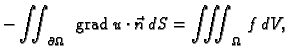
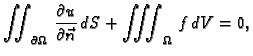
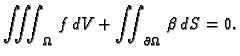
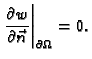

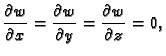
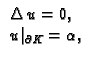
![]() i
i ![]()
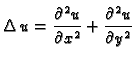
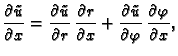
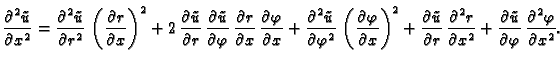
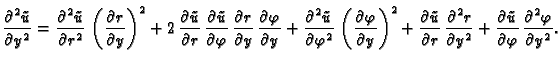
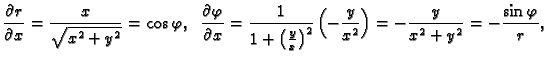
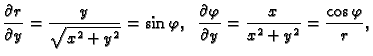
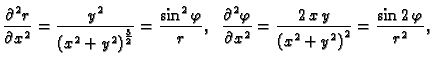
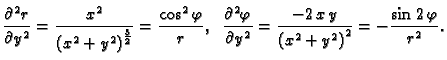
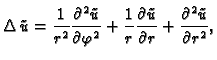
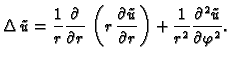
![]() rubni uvjet se može zapisati
ovako
rubni uvjet se može zapisati
ovako
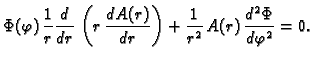
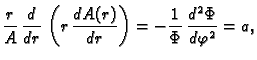
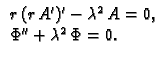
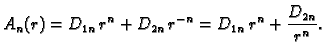
![]() ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
ne mora zadovoljavati rubni uvjet. Zato pretpostavimo
rješenje rubnog problema u obliku
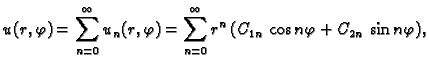
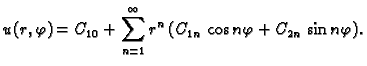
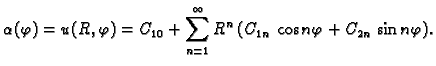
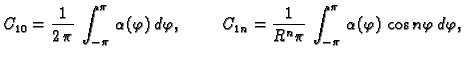
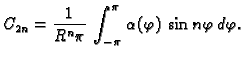
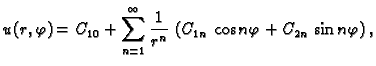
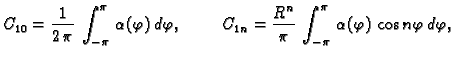
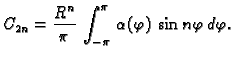
![$\displaystyle u(r,\varphi) = C_{0} + D_{0}\,\ln r + \sum_{n=1}^{\infty}
\left[\...
...n\varphi + \left(C_{2n}\,r^n + \frac{D_{2n}}{r^n}\right)\,\sin
n\varphi\right].$](img2190.gif)
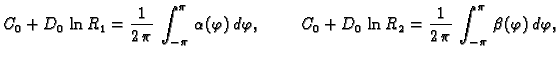
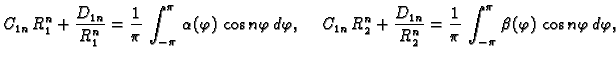
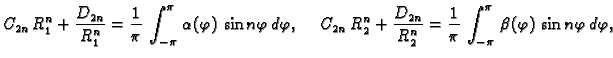
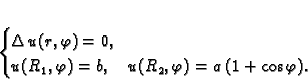
![$\displaystyle u(r,\varphi) = C_{0} + D_{0}\,\ln r + \sum_{n=1}^{\infty}
\left[\...
...n\varphi + \left(C_{2n}\,r^n + \frac{D_{2n}}{r^n}\right)\,\sin
n\varphi\right],$](img2200.gif)
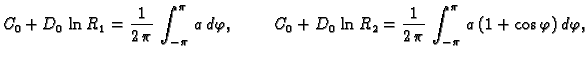
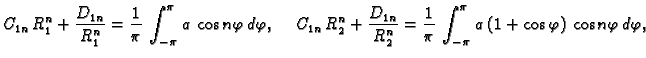
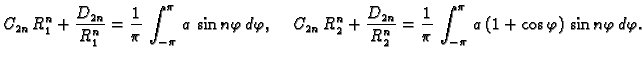
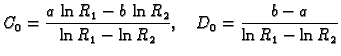
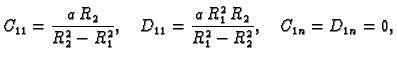 za
za 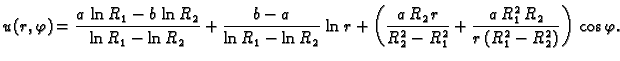
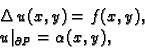
![]() i da je
i da je
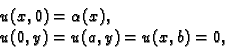
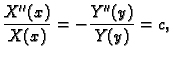
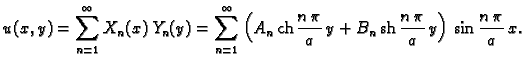
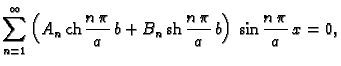
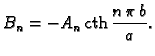
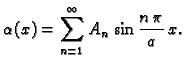
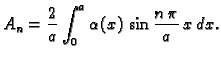
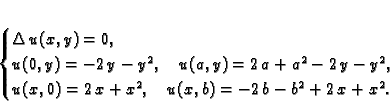
![]() Stavimo
Stavimo
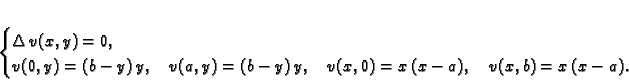
![]() rješenje rubnog problema
rješenje rubnog problema
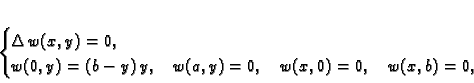
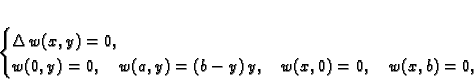
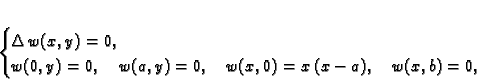
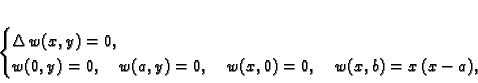
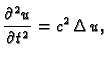
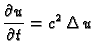
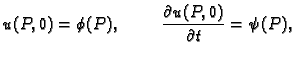
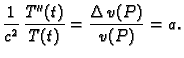
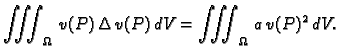
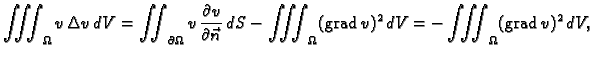
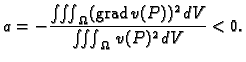
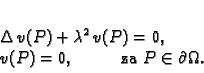
![]() i
i ![]() dvije međusobno različite vlastite
vrijednosti, i
dvije međusobno različite vlastite
vrijednosti, i ![]() odnosno
odnosno ![]() pripadne vlastite funkcije. Tada
pripadne vlastite funkcije. Tada
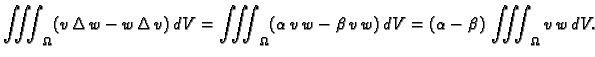
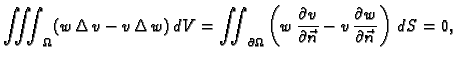
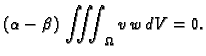
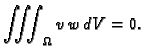
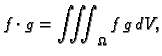
![]() vlastite
vrijednosti, a
vlastite
vrijednosti, a
![]() vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
vlastite funkcije rubnog
problema. Tada vremenska jednadžba glasi
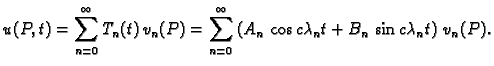
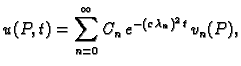
![]() ravnotežni položaj membrane, tj. rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije
ravnotežni položaj membrane, tj. rješenje gornjeg problema. Da bi se membrana pomakla iz tog
položaja, potrebno je izvršiti neki rad. Taj rad ovisi o veličini
perturbacije ![]() Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i
Budući da je u novom položaju membrana i
dalje učvršćena na rubu, mora i ![]() biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka
biti dopustiva funkcija. Rad,
koji izvrši vanjska sila uslijed pomaka ![]() je
je
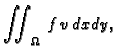
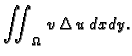
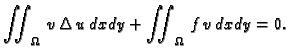
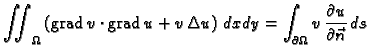
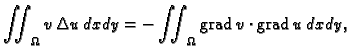
![]() rješava rubni problem
(2.56), onda za svaku dopustivu funkciju
rješava rubni problem
(2.56), onda za svaku dopustivu funkciju ![]() vrijedi
(2.57). Također vrijedi i obrat. Ako
vrijedi
(2.57). Također vrijedi i obrat. Ako ![]() sa svojstvom
sa svojstvom
![]() zadovoljava (2.57) za svaku
dopustivu funkciju
zadovoljava (2.57) za svaku
dopustivu funkciju ![]() onda
onda ![]() rješava rubni problem (2.56).
rješava rubni problem (2.56).
![]() i neka
je
i neka
je
![]() Tada je prema prvoj Greenovoj formuli
Tada je prema prvoj Greenovoj formuli
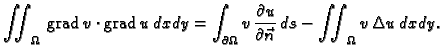
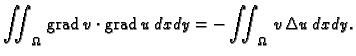
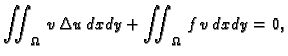
![$\displaystyle \iint_{\Omega}\,\left[\Delta u + f\right]\,v\,dxdy = 0,$](img2314.gif)
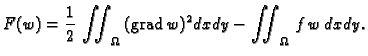
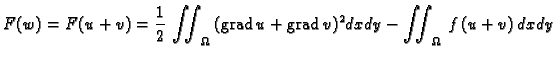
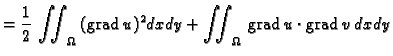
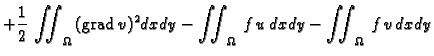
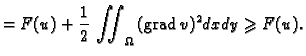
![]() koja minimizira funkcional
koja minimizira funkcional
![]() i zadovoljava rubni uvjet
i zadovoljava rubni uvjet
![]() mora
zadovoljavati Bernoullijev princip, tj. (2.57). Pretpostavimo da
mora
zadovoljavati Bernoullijev princip, tj. (2.57). Pretpostavimo da ![]() ima tražena svojstva, i
stavimo
ima tražena svojstva, i
stavimo
![]() gdje je
gdje je ![]() perturbacija (funkcija iz klase
dopustivih). Funkcional
perturbacija (funkcija iz klase
dopustivih). Funkcional ![]() poprima minimum na funkciji
poprima minimum na funkciji ![]() pa prema
tome funkcija
pa prema
tome funkcija
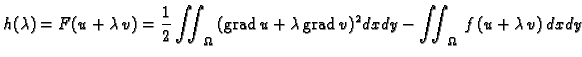
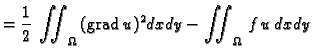
![% latex2html id marker 37180
$\displaystyle +
\lambda{}\left[\iint_{\Omega}\,{\rm grad\,}u\cdot{\rm grad\,}v\,dxdy - \iint_{\Omega}\,
f\,v\,dxdy\right]$](img2332.gif)