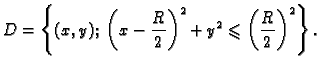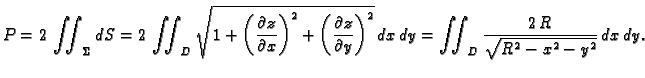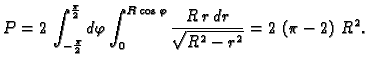Next: Plošni integral 2. vrste
Up: Plošni integrali
Previous: Plošni integrali
Contents
Index
Subsections
Umjesto da definiramo glatku plohu radije promotrimo kako se ploha
može zadati. Primjeri, koje ćemo raditi, bit će primjeri glatkih
ploha ili po dijelovima glatkih ploha. Napomenimo da jedno od važnih
svojstava glatke plohe je da ima u svakoj točki tangencijalnu
ravninu. Po dijelovima glatka ploha je neprekidna ploha, koja se
sastoji od konačno mnogo glatkih ploha.
Neka je  područje u
područje u 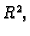 i neka
i neka
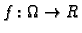 ima neprekidne parcijalne derivacije po
ima neprekidne parcijalne derivacije po  i
i 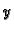 na
na 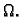 Graf takve funkcije
Graf takve funkcije  zovemo glatkom
plohom. Jednadžba takve plohe je
zovemo glatkom
plohom. Jednadžba takve plohe je
Primjer 5.1
Graf funkcije
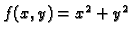
je rotacijski paraboloid, čija je
jednadžba
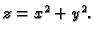
(v. sliku
1.1.3)
Primjer 5.2
Graf funkcije
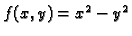
je hiperbolički paraboloid (sedlasta
ploha), čija je jednadžba
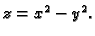
(v. sliku
4)
U daljnjem izlaganju će nam biti važan vektor normale na
tangencijalnu ravninu u točki  ovako zadane plohe
ovako zadane plohe
Na opisani način ne možemo zadati sferu, već samo neke njezine
dijelove. Općenitije zadavati glatku plohu može se
implicitno.
Neka je  područje u
područje u 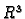 i
i
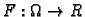 funkcija klase
funkcija klase
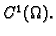 Tada je jednadžbom
Tada je jednadžbom
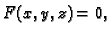 |
(5.1) |
uz uvjet da ova jednadžba ima bar jedno rješenje
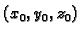 i
da je
zadana funkcija
i
da je
zadana funkcija  klase
klase 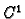 na nekom području
na nekom području  u ravnini
u ravnini 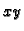 takva da vrijedi
tj. varijablu
takva da vrijedi
tj. varijablu 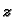 možemo shvatiti kao funkciju
od
možemo shvatiti kao funkciju
od  i
i 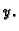 (To je zapravo teorem o implicitno zadanoj funkciji; v.
1.4.3.)
(To je zapravo teorem o implicitno zadanoj funkciji; v.
1.4.3.)
Uz neke druge uvjete može se  shvatiti kao
funkcija od
shvatiti kao
funkcija od 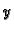 i
i 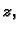 ili
ili 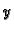 kao funkcija od
kao funkcija od  i
i 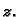 Ostajući,
međutim, na jednadžbi (5.1), i zahtijevajući da je
Ostajući,
međutim, na jednadžbi (5.1), i zahtijevajući da je
dobivamo
skup točaka  u prostoru čiji su pojedini dijelovi grafovi
funkcija od dvije varijable, jer zadnja nejednakost osigurava da je u
svakoj točki bar jedna parcijalna derivacija različita od
u prostoru čiji su pojedini dijelovi grafovi
funkcija od dvije varijable, jer zadnja nejednakost osigurava da je u
svakoj točki bar jedna parcijalna derivacija različita od 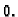 Skup
Skup
 zovemo glatkom plohom.
zovemo glatkom plohom.
Primjer 5.3
Sfera sa središtem u ishodištu i radiusom
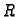
se implicitno zadaje
jednadžbom
Rješenje. U ovom slučaju je
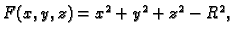 pa je
pa je
Tako je gornjom jednadžbom doista zadana glatka ploha.
Ako je ploha zadana na taj način, onda se vektor normale računa po
formuli
Također, glatku plohu možemo zadati parametrizacijom.
Neka je  područje u
područje u 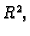 i
i
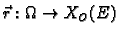 vektorska funkcija klase
vektorska funkcija klase
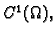 takva da je
takva da je
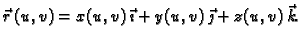 |
(5.2) |
U tom slučaju plohu čini skup točaka u prostoru
Uređeni par
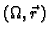 područja
područja  i vektorske funkcije
i vektorske funkcije
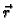 zove se
parametrizacija plohe
zove se
parametrizacija plohe  .
.
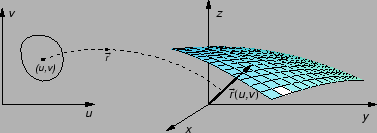
Podsjetimo se,
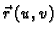 predstavlja radijvektor do točke na
plohi, a
predstavlja radijvektor do točke na
plohi, a
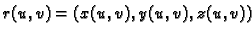 je točka na plohi, tj. vrh
radijvektora.
je točka na plohi, tj. vrh
radijvektora.
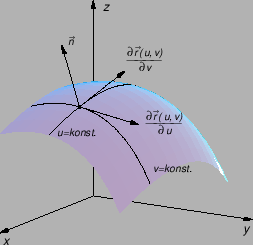
Ako u formulu (5.2) stavimo
 konst.
konst.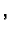 onda
onda 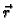 postaje vektorska funkcija jedne varijable. Pomoću takvih funkcija se parametriziraju krivulje. Tako dobivene krivulje (za razne vrijednosti od
postaje vektorska funkcija jedne varijable. Pomoću takvih funkcija se parametriziraju krivulje. Tako dobivene krivulje (za razne vrijednosti od 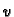 ) se zovu
) se zovu 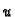 -krivulje. Ako stavimo
-krivulje. Ako stavimo
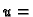 konst.
konst.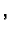 onda na isti način dobivamo drugu familiju krivulja. Te krivulje zovemo
onda na isti način dobivamo drugu familiju krivulja. Te krivulje zovemo 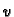 -krivuljama.
-krivuljama.
Primjer 5.4
Sfera sa središtem u ishodištu, radiusa
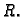
Rješenje. Ova sfera u sfernom koordinatnom sustavu ima
jednadžbu 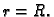 Prema tome parametrizacija je dana s
Prema tome parametrizacija je dana s
gdje je područje

određeno s
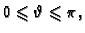
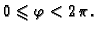
Primjer 5.5
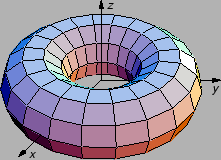
Torus s velikim radiusom
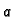
i malim radiusom
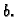
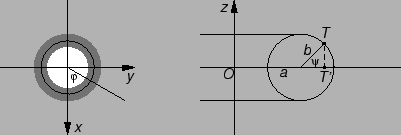
Rješenje.
Slika lijevo dolje je torus gledan s vrha osi
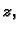
dok desna
predstavlja poprečni presjek jednog dijela torusa.
Prema ovim slikama koordinate točke
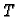
su dane s
Prema desnoj slici
Tako imamo parametrizaciju torusa
gdje je područje

određeno sa
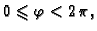
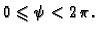
Primjer 5.6
Helikoidalna ploha, tj. ploha koja nastaje kad se od osi
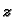
povuku
zrake okomito na os
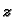
kroz točke helikoide.
Rješenje.
Za parametrizaciju nam može poslužiti parametrizacija helikoide
Iz definicije slijedi da je dovoljno shvatiti
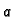
kao varijablu. Dakle
gdje je područje

određeno sa
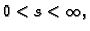
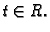
Ako je ploha zadana parametarski, vektor normale se računa
kao vektorski produkt.
gdje je
Da ploha parametarski zadana bude glatka, nužan uvjet je
Neka je  glatka ploha, i neka je na plohi definirana
gustoća mase
glatka ploha, i neka je na plohi definirana
gustoća mase 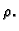 Interesira nas masa te plohe.
Interesira nas masa te plohe.
Podijelimo  na manje dijelove
na manje dijelove
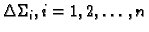 (v. 5.1.2). Na svakom od dijelova
(v. 5.1.2). Na svakom od dijelova
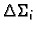 odaberemo proizvoljnu točku
odaberemo proizvoljnu točku 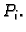 Masa dijela
Masa dijela
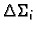 je približno
je približno
gdje
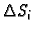 označava površinu dijela
označava površinu dijela
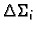 plohe
plohe
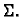 Ukupna masa plohe je približno
Ukupna masa plohe je približno
Sada dijelimo plohu na sve manje dijelove tako da
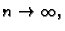 i da se pri tom dijelovi
i da se pri tom dijelovi
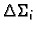 stežu na točke. Ako tada
stežu na točke. Ako tada
teži prema nekom broju 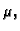 onda je taj broj masa plohe
onda je taj broj masa plohe
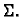
Neka je  glatka ploha, i neka je na plohi definirana funkcija
glatka ploha, i neka je na plohi definirana funkcija
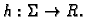 Podijelimo
Podijelimo  na manje dijelove
na manje dijelove
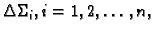
i na svakom od dijelova
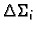 odaberemo proizvoljnu točku
odaberemo proizvoljnu točku 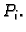 Uočimo broj
gdje
Uočimo broj
gdje
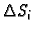 označava površinu dijela plohe
označava površinu dijela plohe
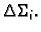 Sada dijelimo plohu na sve manje dijelove tako da
Sada dijelimo plohu na sve manje dijelove tako da
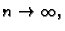 i da se pri tom dijelovi
i da se pri tom dijelovi
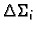 stežu na točke. Ako tada
stežu na točke. Ako tada 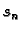 teži prema nekom broju
teži prema nekom broju 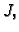 onda taj broj zovemo plošnim
integralom 1. vrste funkcije
onda taj broj zovemo plošnim
integralom 1. vrste funkcije 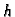 po plohi
po plohi 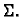 Pišemo
Pišemo
Računanje plošnog integrala 1. vrste
Neka je
![$ I=[a,b]\times [c,d],$](img1107.gif) neka je ploha
neka je ploha  zadana kao graf
funkcije
zadana kao graf
funkcije
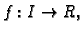 jednadžbom
jednadžbom
i neka je na plohi definirana funkcija 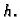 Podijelimo
Podijelimo 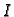 na male pravokutnike dijeleći
segmente
na male pravokutnike dijeleći
segmente
![$ [a,b],[c,d]$](img2438.gif) na podsegmente.
Ova podjela čini mrežu
malih pravokutnika
na podsegmente.
Ova podjela čini mrežu
malih pravokutnika
![$ I_{ij}=[x_{i-1},x_i]\times [y_{j-1},y_j]$](img2441.gif) na
na 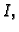 koja inducira mrežu
koja inducira mrežu
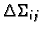 dijelova plohe
dijelova plohe 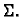
Slika 5.1:
Podjela pravokutnika.
|
|
Uočimo jedan vrh dijela
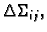 i označimo ga s
i označimo ga s
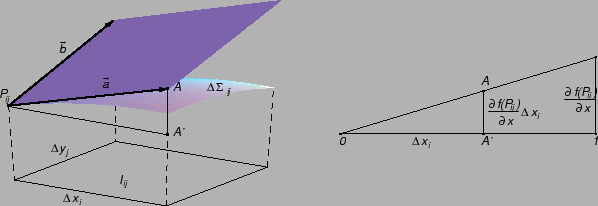
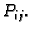 Postavimo tangencijalnu ravninu na plohu u točki
Postavimo tangencijalnu ravninu na plohu u točki 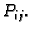 Površina dijela tangencijalne ravnine nad
Površina dijela tangencijalne ravnine nad 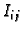 približno je
jednaka površini
približno je
jednaka površini
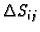 dijela plohe
dijela plohe
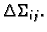 Osim toga izaberimo na dijelu
Osim toga izaberimo na dijelu
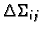 proizvoljnu točku
proizvoljnu točku
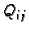 za svaki
za svaki 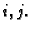 Tada suma, koja se pojavljuje kod
definicije plošnog integrala 1. vrste, postaje
gdje je
Tada suma, koja se pojavljuje kod
definicije plošnog integrala 1. vrste, postaje
gdje je
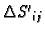 površina onog dijela tangencijalne ravnine na
plohu
površina onog dijela tangencijalne ravnine na
plohu  u točki
u točki 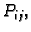 koji se nalazi iznad
koji se nalazi iznad 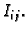 Taj
dio tangencijalne ravnine je paralelogram, pa je njegova površina
jednaka duljini vektorskog produkta vektora duž njegovih stranica s
početkom u točki
Taj
dio tangencijalne ravnine je paralelogram, pa je njegova površina
jednaka duljini vektorskog produkta vektora duž njegovih stranica s
početkom u točki 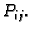 Ti vektori su
Vektorski produkt je
a njegova duljina
Ovdje je
Ti vektori su
Vektorski produkt je
a njegova duljina
Ovdje je
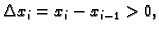
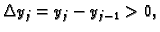 pa je tako
Ova suma se može shvatiti kao integralna
suma dvostrukog integrala funkcije
po pravokutniku
pa je tako
Ova suma se može shvatiti kao integralna
suma dvostrukog integrala funkcije
po pravokutniku 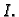 Prema tome, ako je
ploha
Prema tome, ako je
ploha  dana jednadžbom
dana jednadžbom 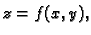 i na njoj definirana
funkcija
i na njoj definirana
funkcija 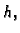 onda plošni integral 1. vrste računamo po formuli
onda plošni integral 1. vrste računamo po formuli
Ako je ploha definirana na zatvorenom području 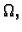 onda,
postupkom sličnom onom kod dvostrukog integrala (v.
2.1.3), možemo zaključiti da je formula za
računanje plošnog integrala 1. vrste
onda,
postupkom sličnom onom kod dvostrukog integrala (v.
2.1.3), možemo zaključiti da je formula za
računanje plošnog integrala 1. vrste
Primijetimo na kraju da se ova formula može kraće zapisati kako
slijedi
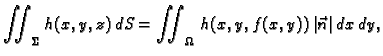 |
(5.3) |
pri čemu je 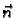 vektor normale na plohu, i to upravo onaj koji
se dobije iz jednadžbe plohe kao
vektor normale na plohu, i to upravo onaj koji
se dobije iz jednadžbe plohe kao
Primjer 5.7
Izračunati
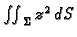
po dijelu plohe
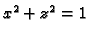
odsječene valjkom
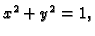
a koja se nalazi iznad
ravnine
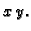
Rješenje. Imamo
pa je
Ako je ploha zadana parametarski, i njezina parametrizacija je
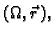 onda je vektor normale
onda je vektor normale
pa je formula za računanje
Duljina vektorskog produkta se može izračunati iz sljedeće
formule
Dakle, ako uvedemo sljedeće oznake
onda je duljina vektora normale
pa se plošni integral 1. vrste računa po formuli
Primjer 5.8
Izračunati
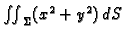
po sferi
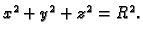
Rješenje. Parametrizacija sfere je
Odatle
Tako je
Formule za računanje pokazuju da plošni integral 1. vrste ima ista
svojstva kao dvostruki integral.
Specijalno, ako je
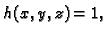 onda plošni integral funkcije
onda plošni integral funkcije 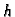 po
plohi
po
plohi  možemo shvatiti kao masu materijalne plohe čija je
gustoća mase konstantna i jednaka
možemo shvatiti kao masu materijalne plohe čija je
gustoća mase konstantna i jednaka 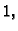 pa je
masa brojčano jednaka površini plohe. Tako imamo sljedeće
formule za računanje površine plohe.
pa je
masa brojčano jednaka površini plohe. Tako imamo sljedeće
formule za računanje površine plohe.
Ako je ploha  zadana eksplicitno,
zadana eksplicitno, 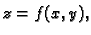 onda je
površina
onda je
površina
Ako je ploha  zadana parametarski,
zadana parametarski,
onda je površina
Primjer 5.9
Naći površinu sfere radiusa
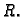
Rješenje. U prethodnom primjeru smo našli da je
pa je
Primjer 5.10
Naći površinu torusa.
Rješenje. Parametrizacija torusa je
pa je
Tako je površina torusa
- 1.
- Na koje načine se može zadati glatka ploha, i kako se u tim
slučajevima računa vektor normale?
- 2.
- Kako se definira plošni integral 1. vrste? Koji problem
rješava?
- 3.
- Kako se računa plošni integral 1. vrste ako je ploha zadana
eksplicitno?
- 4.
- Kako se računa plošni integral 1. vrste ako je ploha zadana
parametarski?
- 5.
- Što predstavljaju veličine
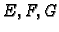 ?
?
- 6.
- Koju ulogu ima vektor normale na plohu? Da li plošni integral
1. vrste ovisi o smjeru vektora normale?
- 7.
- Kako se može izračunati površina plohe?
- 1.
- Naći središte mase gornje polusfere
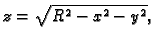 ako je
gustoća mase jednaka udaljenosti od osi
ako je
gustoća mase jednaka udaljenosti od osi 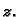
Rješenje. Zbog simetrije problema, očito je
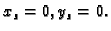
gdje je 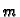 masa plohe, a
masa plohe, a 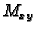 statički moment u odnosu na
ravninu
statički moment u odnosu na
ravninu 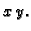 pa je, prelaskom u cilindrični koordinatni sustav,
Tako je
pa je, prelaskom u cilindrični koordinatni sustav,
Tako je
- 2.
- Naći površinu dijela sfere
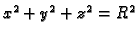 isječenog cilindrom
isječenog cilindrom
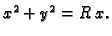 (v. sliku 2.14)
(v. sliku 2.14)
Rješenje. Ploha se sastoji od dva dijela, koji su jedan drugom simetrični u
odnosu na ravninu 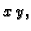 pa je dovoljno izračunati površinu jednog
dijela, na pr. onog određenog formulom
pa je dovoljno izračunati površinu jednog
dijela, na pr. onog određenog formulom
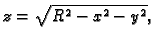 i
područjem
i
područjem
Prelaskom na polarne koordinate u ravnini imamo





Next: Plošni integral 2. vrste
Up: Plošni integrali
Previous: Plošni integrali
Contents
Index
Salih Suljagic
2000-03-11
![]() područje u
područje u ![]() i neka
i neka
![]() ima neprekidne parcijalne derivacije po
ima neprekidne parcijalne derivacije po ![]() i
i ![]() na
na ![]() Graf takve funkcije
Graf takve funkcije ![]() zovemo glatkom
plohom. Jednadžba takve plohe je
zovemo glatkom
plohom. Jednadžba takve plohe je
![]() ovako zadane plohe
ovako zadane plohe
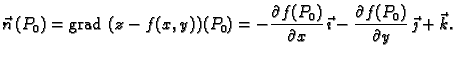
![]() područje u
područje u ![]() i
i
![]() funkcija klase
funkcija klase
![]() Tada je jednadžbom
Tada je jednadžbom
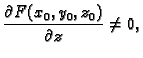
![]() shvatiti kao
funkcija od
shvatiti kao
funkcija od ![]() i
i ![]() ili
ili ![]() kao funkcija od
kao funkcija od ![]() i
i ![]() Ostajući,
međutim, na jednadžbi (5.1), i zahtijevajući da je
Ostajući,
međutim, na jednadžbi (5.1), i zahtijevajući da je
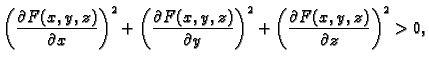
![]() pa je
pa je
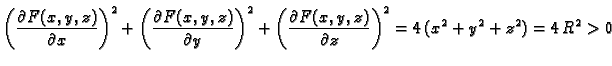
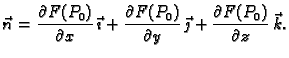
![]() područje u
područje u ![]() i
i
![]() vektorska funkcija klase
vektorska funkcija klase
![]() takva da je
takva da je
![]() područja
područja ![]() i vektorske funkcije
i vektorske funkcije
![]() zove se
parametrizacija plohe
zove se
parametrizacija plohe ![]() .
.
![]() konst.
konst.![]() onda
onda ![]() postaje vektorska funkcija jedne varijable. Pomoću takvih funkcija se parametriziraju krivulje. Tako dobivene krivulje (za razne vrijednosti od
postaje vektorska funkcija jedne varijable. Pomoću takvih funkcija se parametriziraju krivulje. Tako dobivene krivulje (za razne vrijednosti od ![]() ) se zovu
) se zovu ![]() -krivulje. Ako stavimo
-krivulje. Ako stavimo
![]() konst.
konst.![]() onda na isti način dobivamo drugu familiju krivulja. Te krivulje zovemo
onda na isti način dobivamo drugu familiju krivulja. Te krivulje zovemo ![]() -krivuljama.
-krivuljama.
![]() Prema tome parametrizacija je dana s
Prema tome parametrizacija je dana s

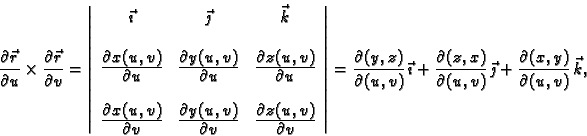
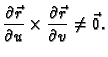
![]() glatka ploha, i neka je na plohi definirana
gustoća mase
glatka ploha, i neka je na plohi definirana
gustoća mase ![]() Interesira nas masa te plohe.
Interesira nas masa te plohe.
![]() na manje dijelove
na manje dijelove
![]() (v. 5.1.2). Na svakom od dijelova
(v. 5.1.2). Na svakom od dijelova
![]() odaberemo proizvoljnu točku
odaberemo proizvoljnu točku ![]() Masa dijela
Masa dijela
![]() je približno
je približno
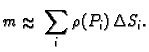
![]() i da se pri tom dijelovi
i da se pri tom dijelovi
![]() stežu na točke. Ako tada
stežu na točke. Ako tada
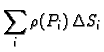
![]() glatka ploha, i neka je na plohi definirana funkcija
glatka ploha, i neka je na plohi definirana funkcija
![]() Podijelimo
Podijelimo ![]() na manje dijelove
na manje dijelove
![]()
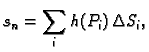
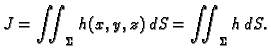
![]() neka je ploha
neka je ploha ![]() zadana kao graf
funkcije
zadana kao graf
funkcije
![]() jednadžbom
jednadžbom
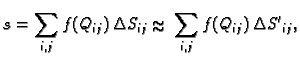
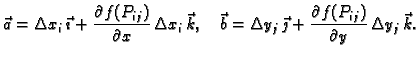
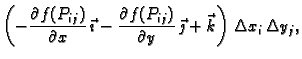
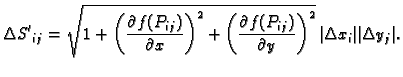
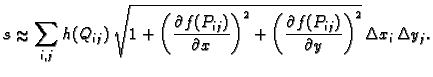
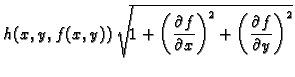
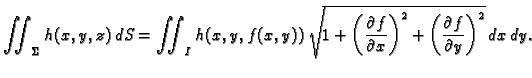
![]() onda,
postupkom sličnom onom kod dvostrukog integrala (v.
2.1.3), možemo zaključiti da je formula za
računanje plošnog integrala 1. vrste
onda,
postupkom sličnom onom kod dvostrukog integrala (v.
2.1.3), možemo zaključiti da je formula za
računanje plošnog integrala 1. vrste
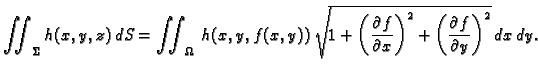
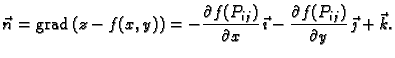
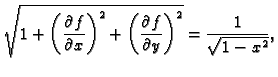
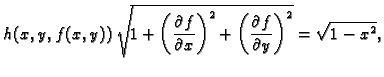
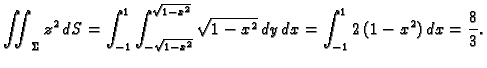
![]() onda je vektor normale
onda je vektor normale
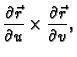
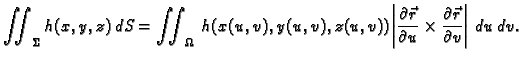
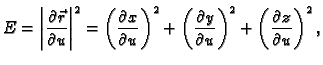
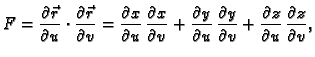
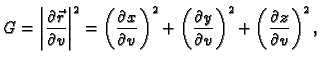
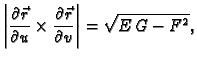
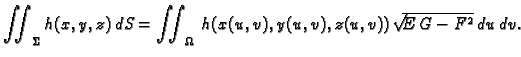
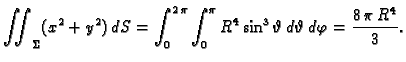
![]() onda plošni integral funkcije
onda plošni integral funkcije ![]() po
plohi
po
plohi ![]() možemo shvatiti kao masu materijalne plohe čija je
gustoća mase konstantna i jednaka
možemo shvatiti kao masu materijalne plohe čija je
gustoća mase konstantna i jednaka ![]() pa je
masa brojčano jednaka površini plohe. Tako imamo sljedeće
formule za računanje površine plohe.
pa je
masa brojčano jednaka površini plohe. Tako imamo sljedeće
formule za računanje površine plohe.
![]() zadana eksplicitno,
zadana eksplicitno, ![]() onda je
površina
onda je
površina
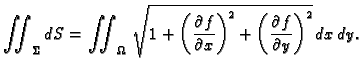
![]() zadana parametarski,
zadana parametarski,
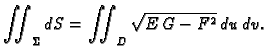
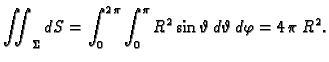
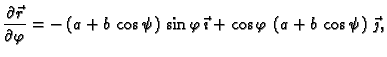
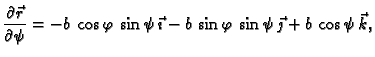
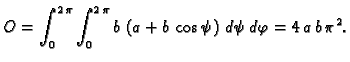
![]()
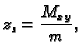
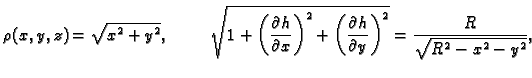
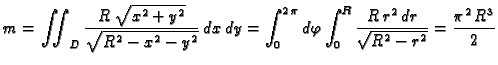
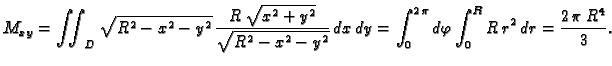
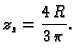
![]() pa je dovoljno izračunati površinu jednog
dijela, na pr. onog određenog formulom
pa je dovoljno izračunati površinu jednog
dijela, na pr. onog određenog formulom
![]() i
područjem
i
područjem