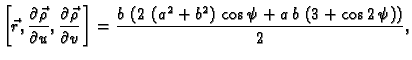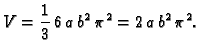Next: Primjene teorema o divergenciji
Up: Plošni integrali
Previous: Plohe. Plošni integral 1.
Contents
Index
Subsections
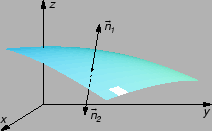
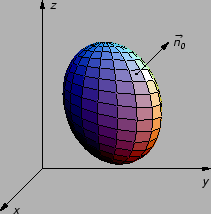
Neka je  glatka ploha. U svakoj točki na plohi postoji
tangencijalna ravnina, pa prema tome u svakoj točki na plohu mogu se
postaviti dva jedinična vektora normale.
glatka ploha. U svakoj točki na plohi postoji
tangencijalna ravnina, pa prema tome u svakoj točki na plohu mogu se
postaviti dva jedinična vektora normale.
Izborom u svakoj točki
jednoga od njih kažemo da je dana orijentacija plohe. To se
može učiniti na beskonačno mnogo načina, no nas će interesirati
samo oni od njih u kojima je tako određeno polje vektora normala
neprekidno. Plohe koje je moguće na taj način orijentirati zovu se
orijentabilne plohe. Postoje plohe kod kojih to nije moguće
učiniti.
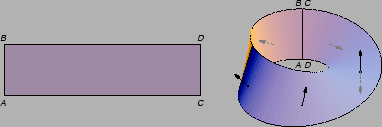
Ova ploha se zove Möbiusova vrpca. Ako krenemo po
srednjoj liniji ove plohe iz jedne točke, izabravši u njoj jedan od
dva moguća jedinična vektora normale, stići ćemo ponovno u tu
točku, ali s druge strane plohe. To pokazuje da se na toj plohi ne
može izabrati neprekidna orijentacija. Takve se plohe zovu
neorijentabilne plohe.
Nas će zanimati samo orijentabilne plohe. Orijentiranu plohu
 ćemo označavati s
ćemo označavati s
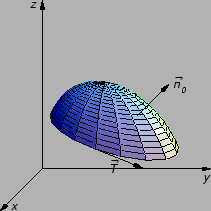
Neka se u nekom području u prostoru giba fluid. Njegovo gibanje je
određeno vektorskim poljem brzina  Pretpostavimo da je
gibanje stacionarno tj. da se
vektorsko polje brzina ne mijenja s vremenom (brzine u pojedinim
točkama ne ovise o vremenu). Zamislimo u području gibanja
orijentiranu plohu
Pretpostavimo da je
gibanje stacionarno tj. da se
vektorsko polje brzina ne mijenja s vremenom (brzine u pojedinim
točkama ne ovise o vremenu). Zamislimo u području gibanja
orijentiranu plohu 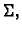 i neka je
i neka je 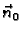 vektorsko polje
jediničnih normala na plohu
vektorsko polje
jediničnih normala na plohu 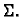 Interesira nas ukupan tok
fluida kroz plohu
Interesira nas ukupan tok
fluida kroz plohu  u jedinici vremena. Za protok količine
fluida, osim brzine potrebno je znati i masu fluida. Neka je dakle
dana gustoća mase fluida
u jedinici vremena. Za protok količine
fluida, osim brzine potrebno je znati i masu fluida. Neka je dakle
dana gustoća mase fluida 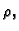 i neka ona također ne ovisi o
vremenu. Nađimo tok fluida kroz jedan djelić plohe. Uočimo
sljedeću sliku.
i neka ona također ne ovisi o
vremenu. Nađimo tok fluida kroz jedan djelić plohe. Uočimo
sljedeću sliku.
Čestica fluida u točki 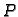 prijeđe u jedinici vremena put od točke
prijeđe u jedinici vremena put od točke
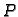 do vrha vektora
do vrha vektora
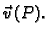 Budući da se, zbog neprekidnosti
brzine, bliske čestice gibaju približno paralelno i približno
jednako daleko, kroz mali dio plohe
Budući da se, zbog neprekidnosti
brzine, bliske čestice gibaju približno paralelno i približno
jednako daleko, kroz mali dio plohe
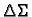 prođe u jedinici
vremena količina fluida koji ispuni približno ovu kvaziprizmu na
slici. Njezin volumen je produkt površine baze i visine, koja je
jednaka duljini projekcije vektora brzine
prođe u jedinici
vremena količina fluida koji ispuni približno ovu kvaziprizmu na
slici. Njezin volumen je produkt površine baze i visine, koja je
jednaka duljini projekcije vektora brzine
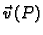 na pravac kroz
vektor normale
na pravac kroz
vektor normale
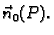 Kako je vektor
Kako je vektor
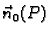 jediničan, visina je apsolutna vrijednost skalarnog produkta
No, osim količine fluida, nas interesira i smjer gibanja. Zato
nećemo uzeti apsolutnu vrijednost, već samo skalarni
produkt. Njegova pozitivnost znači da fluid protječe na onu stranu
na kojoj je vektor normale, a negativnost da fluid protječe na
suprotnu stranu. Masa fluida koja protekne u jedinici vremena kroz
uočeni djelić plohe približno je jednaka umnošku volumena i
gustoće mase u točki
jediničan, visina je apsolutna vrijednost skalarnog produkta
No, osim količine fluida, nas interesira i smjer gibanja. Zato
nećemo uzeti apsolutnu vrijednost, već samo skalarni
produkt. Njegova pozitivnost znači da fluid protječe na onu stranu
na kojoj je vektor normale, a negativnost da fluid protječe na
suprotnu stranu. Masa fluida koja protekne u jedinici vremena kroz
uočeni djelić plohe približno je jednaka umnošku volumena i
gustoće mase u točki 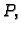 dakle
gdje je
dakle
gdje je 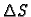 površina dijela plohe
površina dijela plohe
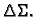 Greška će biti to manja što je promatrani djelić plohe manji.
Da dobijemo ukupni tok, podijelimo plohu
Greška će biti to manja što je promatrani djelić plohe manji.
Da dobijemo ukupni tok, podijelimo plohu  na mnogo malih
dijelova
na mnogo malih
dijelova
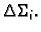 Ukupni tok kroz plohu je tada približno
jednak
Očekujemo da će suma na desnoj strani biti to bliža pravoj masi
fluida protekloj kroz plohu, što je podjela plohe na dijelove
finija.
Ukupni tok kroz plohu je tada približno
jednak
Očekujemo da će suma na desnoj strani biti to bliža pravoj masi
fluida protekloj kroz plohu, što je podjela plohe na dijelove
finija.
Neka je dana orijentirana ploha
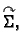 tj. neka je na plohi
tj. neka je na plohi
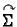 definirano
neprekidno vektorsko polje jediničnih vektora normala
definirano
neprekidno vektorsko polje jediničnih vektora normala
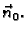 Neka je, osim toga, na plohi
Neka je, osim toga, na plohi
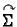 zadano vektorsko polje
zadano vektorsko polje 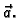 Podijelimo plohu
Podijelimo plohu  na manje
dijelove
na manje
dijelove
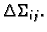 Odaberimo na
Odaberimo na
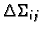 točku
točku 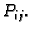 Uočimo sumu
Uočimo sumu
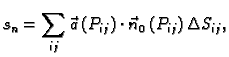 |
(5.4) |
gdje je
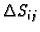 površina dijela plohe
površina dijela plohe
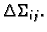 Broj
Broj 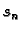 ovisi o broju dijelova plohe i
načinu dijeljenja. Pustimo sada da broj dijelova
ovisi o broju dijelova plohe i
načinu dijeljenja. Pustimo sada da broj dijelova
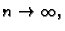 tako da se dijelovi plohe stežu na točku.
Ako u tom slučaju
tako da se dijelovi plohe stežu na točku.
Ako u tom slučaju 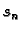 teži k nekom broju
teži k nekom broju 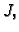 onda taj broj zovemo
plošnim integralom 2. vrste vektorskog polja
onda taj broj zovemo
plošnim integralom 2. vrste vektorskog polja
 na plohi
na plohi 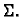 U tom slučaju pišemo
U tom slučaju pišemo
Primijetimo da se 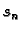 u (5.4) može shvatiti kao
integralna suma plošnog integrala 1. vrste ali skalarne funkcije
u (5.4) može shvatiti kao
integralna suma plošnog integrala 1. vrste ali skalarne funkcije
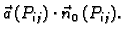 Zahvaljujući formuli
(5.3), plošni integral 2. vrste možemo zapisati
drukčije
Zahvaljujući formuli
(5.3), plošni integral 2. vrste možemo zapisati
drukčije
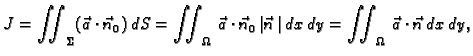 |
(5.5) |
gdje je 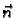 vektorsko polje normala na plohu koje se dobiva iz
jednadžbe plohe bez ikakvog normiranja. Jedino na što treba paziti
je orijentacija plohe.
vektorsko polje normala na plohu koje se dobiva iz
jednadžbe plohe bez ikakvog normiranja. Jedino na što treba paziti
je orijentacija plohe.
Neka je ploha  zadana eksplicitno jednadžbom
zadana eksplicitno jednadžbom
gdje je
![$ f:[a,b]\times [c,d]
\rightarrow R.$](img980.gif) Orijentaciju plohe možemo izabrati tako da vektor normale zatvara s
vektorom
Orijentaciju plohe možemo izabrati tako da vektor normale zatvara s
vektorom 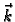 oštar ili tupi kut. U prvom slučaju vektorsko
polje normala
oštar ili tupi kut. U prvom slučaju vektorsko
polje normala 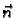 je dano formulom
U drugom slučaju umjesto
je dano formulom
U drugom slučaju umjesto 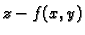 treba uzeti
treba uzeti 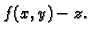 Neka je dano vektorsko polje
Neka je dano vektorsko polje
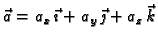 na plohi
na plohi
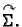 U tom slučaju je
Dakle, plošni integral 2. vrste se računa po formuli
Predznak
U tom slučaju je
Dakle, plošni integral 2. vrste se računa po formuli
Predznak 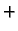 dolazi ako jedinični vektor normale zatvara s vektorom
dolazi ako jedinični vektor normale zatvara s vektorom
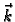 oštar kut, a
oštar kut, a 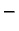 u suprotnom slučaju.
u suprotnom slučaju.
Primjer 5.11
Izračunati
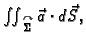
ako
je
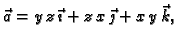
a
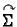
dio plohe
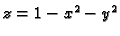
iznad ravnine
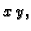
orijentirane tako da vektor normale zatvara oštar kut s vektorom
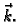
Rješenje. Budući da je ploha orijentirana tako da vektor
normale zatvara oštar kut s vektorom 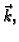 u formuli treba uzeti
u formuli treba uzeti
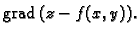 Tako imamo
Tako imamo
Ako je ploha zadana parametarski, onda je vektorsko polje normala
Ako se orijentacija plohe poklapa s onom koju određuje
parametrizacija, onda imamo formulu za računanje
gdje tri vektora u uglatim zagradama predstavlja mješoviti produkt u
tom poretku ili u nekoj cikličkoj permutaciji.
Ako je orijentacija plohe suprotna onoj koju daje parametrizacija,
onda treba uzeti 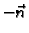 umjasto
umjasto 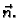
Primjer 5.12
Izračunati
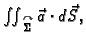
ako je
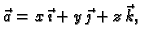
a
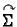
dio središnje sfere
radiusa
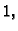
u prvom oktantu, orijentirane tako da vektor normale
zatvara oštar kut s vektorom
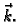
Rješenje. Sferu možemo parametrizirati
Promatrani dio sfere se dobije, ako se uzme
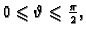
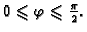
Tada je
Da bismo plohu orijentirali u skladu sa
zahtjevom, pomnožimo vektorski ove vektore
Budući da je komponenta uz vektor
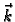
pozitivna kad se
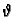
mijenja od 0 do
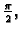
ovo je vektor normale u skladu sa zahtijevanom orijentacijom. Tako je
Dakle,
Veza između plošnih integrala 1. i 2. vrste dana je formulom
Na lijevoj strani
je integral 2. vrste vektorskog polja 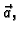 dok je na desnoj
strani integral 1. vrste skalarnog polja
dok je na desnoj
strani integral 1. vrste skalarnog polja
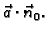 Integral 1. vrste doduše ne ovisi o orijentaciji plohe, međutim o
orijentaciji plohe ovisi skalarno polje
Integral 1. vrste doduše ne ovisi o orijentaciji plohe, međutim o
orijentaciji plohe ovisi skalarno polje
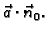 Prilikom suprotne orijentacije vektor
Prilikom suprotne orijentacije vektor 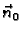 mijenja znak, pa i
skalarno polje također.
mijenja znak, pa i
skalarno polje također.
Polazeći od ove formule, možemo izvesti još jednu formulu za
računanje plošnog integrala 2. vrste. Neka je
Tada je
Brojevi
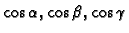 su kosinusi smjera
jediničnog vektora normale na plohu, dakle,
su kosinusi smjera
jediničnog vektora normale na plohu, dakle,
Formule za računanje pokazuju da plošni integral 2. vrste ima ista svojstva kao dvostruki integral. Osim tih svojstava, plošni integral 2. vrste mijenja znak kad se promijeni orijentacija plohe.
Teorem 22
(Teorem o divergenciji)
Neka je

zatvoreno područje u prostoru, čiji je rub
orijentabilna, po dijelovima glatka ploha
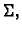
koja samu sebe ne
presijeca. Neka je na

zadano vektorsko polje vanjskih
jediničnih normala. Neka je
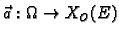
vektorsko polje klase
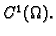
Tada vrijedi formula
Dokaz. Dokažimo teorem u jednom jednostavnom
slučaju. Neka je područje kvadar 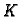 čije su stranice
čije su stranice
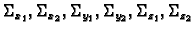 paralelne koordinatnim ravninama.
paralelne koordinatnim ravninama.
Slika 5.2:
Dokaz teorema o divergenciji.
|
|
Označimo s  projekciju kvadra
projekciju kvadra 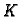 na ravninu
na ravninu 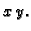
Na isti način dobivamo
Zbrojimo li ove tri jednakosti, dobivamo
Ovaj teorem se naziva još Green-Gaussov ili
Ostrogradski-Green-Gaussov teorem.
Primjer 5.13
Neka je
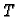
tijelo omeđeno dijelovima ravnina, koje su tangencijalne
ravnine na kuglu radiusa
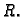
Naći tok vektorskog polja
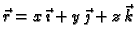
kroz rub
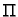
tijela
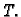
Rješenje. Tok vektorskog polja je
gdje su
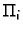
stranice tijela.
Slika 5.3:
Primjer upotrebe teorema o divergenciji.
|
|
Iz slike se vidi da je za proizvoljnu stranicu
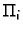
Tako je
gdje
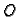
označava oplošje tijela
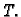
Time smo riješili zadatak, no ako primijenimo teorem o divergenciji
dobivamo usput jedan interesantan rezultat.
gdje je s
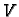
označen volumen tijela
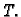
Dakle, kod takvih tijela
omjer oplošja
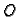
i volumena
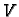
ovisi samo o radiusu upisane kugle.
Da li nešto slično vrijedi u ravnini?
Neka je dana orijentabilna ploha 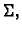 čiji je rub po dijelovima
glatka krivulja
čiji je rub po dijelovima
glatka krivulja 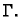 Kažemo da su ploha i njezin rub
koherentno orijentirani, ako, gledano s vrha
vektora normale na plohu u nekoj točki, orijentacija krivulje nalaže
kretanje po krivulji u pozitivnom smjeru, tj. protivno kazaljci na
satu.
Kažemo da su ploha i njezin rub
koherentno orijentirani, ako, gledano s vrha
vektora normale na plohu u nekoj točki, orijentacija krivulje nalaže
kretanje po krivulji u pozitivnom smjeru, tj. protivno kazaljci na
satu.
Teorem 23
(Stokesov teorem)
Neka je

vektorsko polje klase
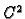
na nekom otvorenom
skupu, koji sadrži plohu
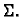
Neka je rub plohe

po
dijelovima glatka krivulja
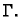
Neka su

i

koherentno orijentirane. Tada vrijedi
odnosno
- 1.
- Što znači orijentirati glatku plohu?
- 2.
- Kad kažemo za plohu da je orijentabilna?
- 3.
- Da li je svaka ploha orijentabilna? Dajte primjer.
- 4.
- Definirajte plošni integral 2. vrste. Koji problem rješava?
- 5.
- Navedite formule za računanje u ovisnosti o načinu zadavanja
plohe.
- 6.
- Koja je veza između plošnih integrala 1. i 2. vrste?
- 7.
- Kako glasi teorem o divergenciji? Dokažite ga.
- 8.
- Kako glasi Stokesov teorem? Što znači da su ploha i njezin rub
koherentno orijentirani?
- 1.
- Neka je tijelo
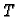 ograničeno po dijelovima glatkom plohom
ograničeno po dijelovima glatkom plohom
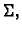 koja samu sebe ne presijeca. Dokazati da je volumen
tijela
koja samu sebe ne presijeca. Dokazati da je volumen
tijela 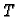 dan formulom
gdje je
dan formulom
gdje je
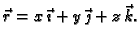
Rješenje.
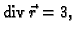 pa po teoremu o divergenciji
pa po teoremu o divergenciji
- 2.
- Naći volumen torusa.
Rješenje. Prema primjeru 5.10, parametrizacija torusa je
a prema prethodnom primjeru
Iz formule za vezu između plošnih integrala 1. i 2. vrste i
formule za računanje plošnog integrala 2. vrste po parametarski
zadanoj plohi, slijedi
Integrira se po torusu, pa je
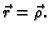 Tako je
i prema tome
Primijetite da je taj broj jednak volumenu kružnog valjka radiusa
baze
Tako je
i prema tome
Primijetite da je taj broj jednak volumenu kružnog valjka radiusa
baze 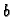 i visine jednake duljini srednje linije torusa.
i visine jednake duljini srednje linije torusa.





Next: Primjene teorema o divergenciji
Up: Plošni integrali
Previous: Plohe. Plošni integral 1.
Contents
Index
Salih Suljagic
2000-03-11
![]() glatka ploha. U svakoj točki na plohi postoji
tangencijalna ravnina, pa prema tome u svakoj točki na plohu mogu se
postaviti dva jedinična vektora normale.
glatka ploha. U svakoj točki na plohi postoji
tangencijalna ravnina, pa prema tome u svakoj točki na plohu mogu se
postaviti dva jedinična vektora normale.
![]() Pretpostavimo da je
gibanje stacionarno tj. da se
vektorsko polje brzina ne mijenja s vremenom (brzine u pojedinim
točkama ne ovise o vremenu). Zamislimo u području gibanja
orijentiranu plohu
Pretpostavimo da je
gibanje stacionarno tj. da se
vektorsko polje brzina ne mijenja s vremenom (brzine u pojedinim
točkama ne ovise o vremenu). Zamislimo u području gibanja
orijentiranu plohu ![]() i neka je
i neka je ![]() vektorsko polje
jediničnih normala na plohu
vektorsko polje
jediničnih normala na plohu ![]() Interesira nas ukupan tok
fluida kroz plohu
Interesira nas ukupan tok
fluida kroz plohu ![]() u jedinici vremena. Za protok količine
fluida, osim brzine potrebno je znati i masu fluida. Neka je dakle
dana gustoća mase fluida
u jedinici vremena. Za protok količine
fluida, osim brzine potrebno je znati i masu fluida. Neka je dakle
dana gustoća mase fluida ![]() i neka ona također ne ovisi o
vremenu. Nađimo tok fluida kroz jedan djelić plohe. Uočimo
sljedeću sliku.
i neka ona također ne ovisi o
vremenu. Nađimo tok fluida kroz jedan djelić plohe. Uočimo
sljedeću sliku.

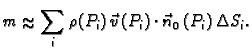
![]() tj. neka je na plohi
tj. neka je na plohi
![]() definirano
neprekidno vektorsko polje jediničnih vektora normala
definirano
neprekidno vektorsko polje jediničnih vektora normala
![]() Neka je, osim toga, na plohi
Neka je, osim toga, na plohi
![]() zadano vektorsko polje
zadano vektorsko polje ![]() Podijelimo plohu
Podijelimo plohu ![]() na manje
dijelove
na manje
dijelove
![]() Odaberimo na
Odaberimo na
![]() točku
točku ![]() Uočimo sumu
Uočimo sumu
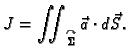
![]() u (5.4) može shvatiti kao
integralna suma plošnog integrala 1. vrste ali skalarne funkcije
u (5.4) može shvatiti kao
integralna suma plošnog integrala 1. vrste ali skalarne funkcije
![]() Zahvaljujući formuli
(5.3), plošni integral 2. vrste možemo zapisati
drukčije
Zahvaljujući formuli
(5.3), plošni integral 2. vrste možemo zapisati
drukčije
![]() zadana eksplicitno jednadžbom
zadana eksplicitno jednadžbom
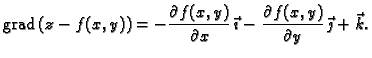
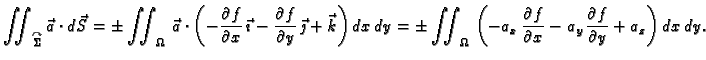
![]() u formuli treba uzeti
u formuli treba uzeti
![]() Tako imamo
Tako imamo
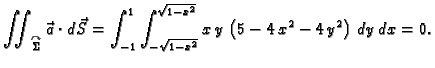
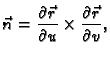
![$\displaystyle \iint_{\overset{\curvearrowright}{\Sigma}}\vec{a}\cdot d\vec{S}=\...
...ial \vec{r}}{\partial u},
\frac{\partial \vec{r}}{\partial v}\,\right]\,du\,dv,$](img2551.gif)
![]() umjasto
umjasto ![]()
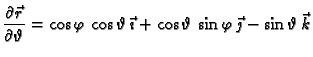
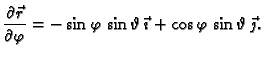
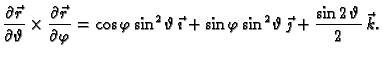
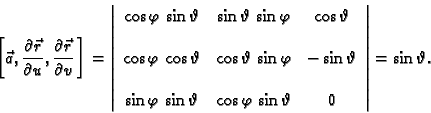
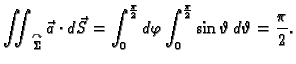
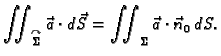
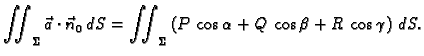
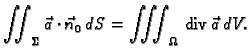
![]() projekciju kvadra
projekciju kvadra ![]() na ravninu
na ravninu ![]()
![$\displaystyle \iiint_K \frac{\partial a_z}{\partial z}\,dx\,dy\,dz =
\iint_D \left[a_z(x,y,z_2) - a_z(x,y,z_1)\right]\,dx\,dy =
\iint_D a_z(x,y,z_2)\,dx\,dy $](img2577.gif)
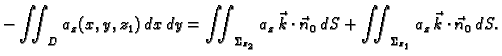
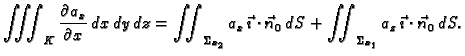
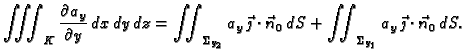
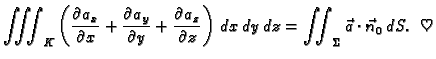
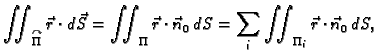
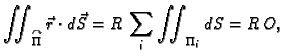
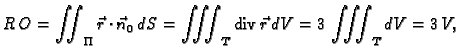
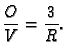
![]() čiji je rub po dijelovima
glatka krivulja
čiji je rub po dijelovima
glatka krivulja ![]() Kažemo da su ploha i njezin rub
koherentno orijentirani, ako, gledano s vrha
vektora normale na plohu u nekoj točki, orijentacija krivulje nalaže
kretanje po krivulji u pozitivnom smjeru, tj. protivno kazaljci na
satu.
Kažemo da su ploha i njezin rub
koherentno orijentirani, ako, gledano s vrha
vektora normale na plohu u nekoj točki, orijentacija krivulje nalaže
kretanje po krivulji u pozitivnom smjeru, tj. protivno kazaljci na
satu.
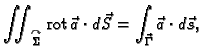
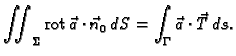
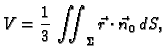
![]() pa po teoremu o divergenciji
pa po teoremu o divergenciji
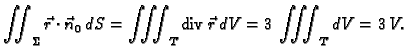
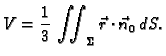
![$\displaystyle V = \iint_{D} \left[\vec{r}, \frac{\partial \vec{\rho}}{\partial u},
\frac{\partial \vec{\rho}}{\partial v}\,\right]\,du\,dv.$](img2599.gif)