Next: Obične diferencijalne jednadžbe
Up: Plošni integrali
Previous: Plošni integral 2. vrste
Contents
Index
Subsections
Iz teorema o divergenciji slijede još neke važne formule.
Na primjer
Analogno
Teorem 24
Neka je
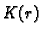
zatvorena kugla sa središtem u točki
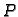
i
radiusom
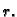
Neka je
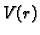
njezin volumen. Neka je
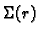
sfera, koja čini rub kugle
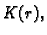
i neka je
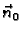
vektorsko polje vanjskih jediničnih normala na plohu
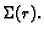
Neka je

vektorsko polje klase
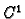
na nekom području koje
sadrži
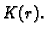
Tada vrijedi
Dokaz. Iz teorema o divergenciji slijedi
Budući da je
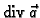 neprekidna funkcija, možemo primijeniti teorem srednje vrijednosti za integrale. Tako imamo
gdje je
neprekidna funkcija, možemo primijeniti teorem srednje vrijednosti za integrale. Tako imamo
gdje je 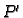 neka točka iz kugle
neka točka iz kugle 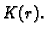 Podijelimo s
Podijelimo s 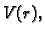 i pustimo da
i pustimo da
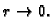 Tada se kugla steže na točku
Tada se kugla steže na točku 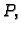 i točka
i točka 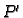 teži k
teži k 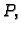 pa prema tome doista vrijedi gornja formula.
pa prema tome doista vrijedi gornja formula.

Prilikom definiranja plošnog integrala 2. vrste razmatrali smo
stacionarno protjecanje fluida. Uočimo proizvoljnu točku 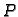 u
području gibanja fluida, i opišimo oko nje zatvorenu kuglu
u
području gibanja fluida, i opišimo oko nje zatvorenu kuglu
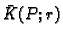 radiusa
radiusa 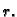 Tok mase fluida u jedinici vremena kroz rub
kugle
Tok mase fluida u jedinici vremena kroz rub
kugle 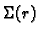 je
je
Prosječna gustoća toka mase se dobije kad se ovaj broj podijeli s
volumenom kugle 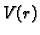 Pravu gustoću u točki
Pravu gustoću u točki 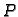 ćemo dobiti kad uzmemo limes ovog
integrala kad
ćemo dobiti kad uzmemo limes ovog
integrala kad 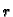 teži k nuli. To je upravo učinjeno u teoremu
24. Dakle možemo zaključiti da
teži k nuli. To je upravo učinjeno u teoremu
24. Dakle možemo zaključiti da
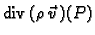 predstavlja gustoću toka mase u jedinici
vremena u točki
predstavlja gustoću toka mase u jedinici
vremena u točki 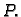 Ako je
Ako je
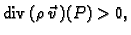 onda u
točki
onda u
točki 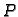 imamo izvor mase, ako je
imamo izvor mase, ako je
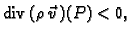 onda
u točki
onda
u točki 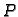 imamo ponor mase, ako je
imamo ponor mase, ako je
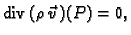 onda u točki
onda u točki 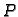 nema niti izvora, niti ponora mase.
nema niti izvora, niti ponora mase.
Pretpostavimo da se fluid giba u nekom području  bez izvora i ponora,
i da to gibanje ovisi i o vremenu (nije stacionarno). Dakle, gustoća
mase je
bez izvora i ponora,
i da to gibanje ovisi i o vremenu (nije stacionarno). Dakle, gustoća
mase je
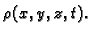 Zamislimo, u području gibanja, fiksno
područje
Zamislimo, u području gibanja, fiksno
područje 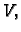 čiji je rub ploha
čiji je rub ploha 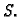
Ukupna masa fluida u 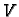 je
Ukupna masa, koja u jedinici vremena izađe iz
je
Ukupna masa, koja u jedinici vremena izađe iz 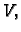 je
S druge strane, ta veličina je jednaka promjeni ukupne mase u
području
je
S druge strane, ta veličina je jednaka promjeni ukupne mase u
području 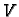 Dakle
odnosno
Prema teoremu o divergenciji to je
odnosno
Budući da je podintegralna funkcija neprekidna, i da smo područje
Dakle
odnosno
Prema teoremu o divergenciji to je
odnosno
Budući da je podintegralna funkcija neprekidna, i da smo područje
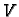 mogli birati proizvoljno, slijedi
Ova jednadžba se zove jednadžba kontinuiteta i jedna je od osnovnih
jednadžbi u hidromehanici.
mogli birati proizvoljno, slijedi
Ova jednadžba se zove jednadžba kontinuiteta i jedna je od osnovnih
jednadžbi u hidromehanici.
Specijalno, ako je fluid nestlačiv (na pr. voda), onda je gustoća
konstanta po prostornim varijablama i po vremenu, pa jednadžba
kontinuiteta postaje
- 1.
- Navedite formule analogne teoremu o divergenciji koje se odnose na
gradijent, rotaciju i Laplace.
- 2.
- Navedite fizikalnu interpretaciju divergencije.
- 3.
- Napišite jednadžbu kontinuiteta, i izvedite je.





Next: Obične diferencijalne jednadžbe
Up: Plošni integrali
Previous: Plošni integral 2. vrste
Contents
Index
Salih Suljagic
2000-03-11
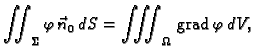
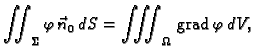
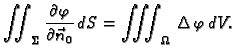
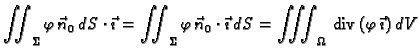
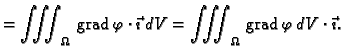
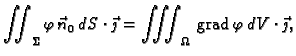
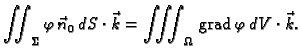
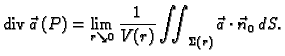
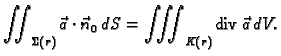
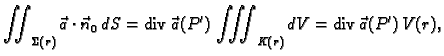
![]() u
području gibanja fluida, i opišimo oko nje zatvorenu kuglu
u
području gibanja fluida, i opišimo oko nje zatvorenu kuglu
![]() radiusa
radiusa ![]() Tok mase fluida u jedinici vremena kroz rub
kugle
Tok mase fluida u jedinici vremena kroz rub
kugle ![]() je
je
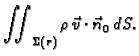
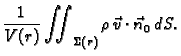
![]() bez izvora i ponora,
i da to gibanje ovisi i o vremenu (nije stacionarno). Dakle, gustoća
mase je
bez izvora i ponora,
i da to gibanje ovisi i o vremenu (nije stacionarno). Dakle, gustoća
mase je
![]() Zamislimo, u području gibanja, fiksno
područje
Zamislimo, u području gibanja, fiksno
područje ![]() čiji je rub ploha
čiji je rub ploha ![]()

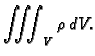
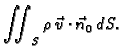
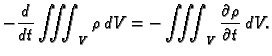
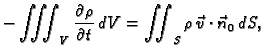
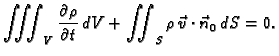
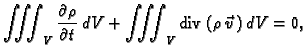
![% latex2html id marker 42551
$\displaystyle \iiint_V \left[\frac{\partial\rho}{\partial t} +
{\rm div\,}(\rho\,\vec{v}\,)\right]\,dV = 0.$](img2638.gif)