Znanstveno-stručni časopis
Hrvatskog društva za geometriju i grafiku

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics




János Pallagi, Benedek Schultz, Jenö Szirmai (jpallagi@math.bme.hu, schultz.benedek@gmail.com, szirmai@math.bme.hu)

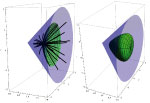
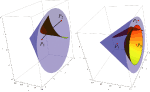
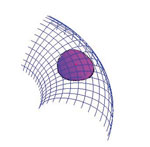
Ekvidistantne plohe u prostoru H2×R

Nakon istraživanja ekvidistanthih ploha ("okomitih simetrala" dviju točaka) u prostoru S2×R (vidi [6]), razmatramo analogni problem u prostoru H2×R iz osam Thurstonovih geometrija. U radu [10] treći je autor odredio geodetske krivulje i kugle prostora H2×R te definirao pojam popunjavanja geodetskim kuglama i njegovu gustoću. Pored toga, razvio je metodu određivanja gustoće popunjavanja geodetskim kuglama za generalizirane Coxeterove grupe prostora H2×R i primijenio taj algoritam na njih. U ovom radu uvodimo pojam ekvidistantne plohe dviju točaka u geometriji H2×R, određujemo njihovu jednadžbu i vizualiziramo neke slučajeve. Slike su napravljene u Wolframovom programu Mathematica.

Ključne riječi: neeuklidske geometrije, geodetska krivulja, geodetska sfera, ekvidistantna ploha u H2×R geometriji

Članak u PDF-u.








Miljenko Lapaine (mlapaine@geof.hr)

Mollweideova kartografska projekcija

Karl Brandan Mollweide (1774-1825) bio je njemački matematičar i astronom. U ovom radu prikazane su formule nazvane po njemu kao Mollweideove formule, a uz njih "dokaz bez riječi". Zatim je definirana Mollweideova kartografska projekcija uz izvod formula na nekoliko različitih načina kako bi se pokazalo da postoji više mogućnosti koje vode do istoga rezultata. Izvedena je generalizacija Mollweideove projekcije koja omogućava dobivanje pseudocilindričnih ekvivalentnih (istopovršinskih) projekcija smještenih u elipsu s bilo kojim unaprijed bzadanim odnosnom njezinih poluosi. Izvedene su i inverzne jednadžbe Mollweideove projekcije.
Najvažniji dio istraživanja svake kartografske projekcije je ustanovljavanje razdiobe deformacija. Stoga su u radu dane formule i grafički prikazi koji daju uvid u razdiobu linearnih i kutnih deformacija Mollweideove projekcije. Na kraju je prikazano nekoliko primjena Mollweideove projekcije. Među njima je i logotip Međunarodnoga kartografskog društva, kao jedan od primjera njezine uspješne primjene.

Ključne riječi: Mollweide, Mollweideova formula, Mollweideova kartografska projekcija

Članak u PDF-u.

 

Márta Szilvási-Nagy, Szilvia Szilvia Béla (szilvasi@math.bme.hu, belus@math.bme.hu)

B-splajn dijelovi koji pristaju na plohe i triangularne mreže

U ovom se radu prikazuje metoda za konstrukciju kvartnog polinoma B-splajn dijela podesnog za analitičke plohe i mreže trokuta. Ulazni podaci su vrijednosti zakrivljenosti i glavni smjerovi u danoj točki plohe, koji se mogu izravno računati za plohu zadanu vektorskom funkcijom.
Za slučaj diskretne reprezentacije plohe, tj. za triangularnu mrežu, odgovarajući ulazni podaci računaju se iz kružne okoline određenog trokuta mreže. Takvi dijelovi mogu zamijeniti dobro definirano područje mreže, i mogu se upotrijebiti npr. u retriangulaciji, simplifikaciji mreže i renderiranju.

Ključne riječi: B-splajn ploha, lokalna aproksimacija plohe, glavne zakrivljenosti, mreža trokuta

Članak u PDF-u.





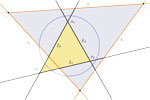
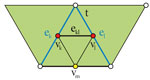
Norman John Wildberger (n.wildberger@unsw.edu.au)

Univerzalna hiperbolička geometrija III: Prvi koraci u projektivnoj geometriji trokuta

Na temelju algebarskog pristupa univerzalne geometrije, uvodimo geometriju trokuta u projektivno-metrički okvir. To rezultira jednim novim oblikom hiperboličke geometrije trokuta. Tri su glavne okosnice: hijerarhije ortocentara, središta upisanih i središta opisanih kružnica, od kojih su posljednje dvije dualne. Primjena ortolinearnih koordinata u formulama ima bitnu ulogu. Istaknuto je pet posebnih točaka (b, z, x, h i s) koje leže na ortogonalnoj osi A. Bogato, kaleidoskopsko gledište karakterizira obradu teme.

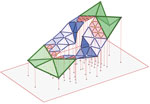
Ključne riječi: univerzalna hiperbolička geometrije, geo metrija trokuta, projektivna geometrija, bilinearna forma, ortolinearne koordinate, središte upisane kružnice, središte opisane kružnice, ortogonalna os

Članak u PDF-u.




Günter Wallner, Franz Gruber (guenter.wallner@uni-ak.ac.at, franz.gruber@uni-ak.ac.at)

Interaktivno modeliranje i razdioba fleksibilnog mehanizma jednakostraničnih trokuta

Prema zahtjevima arhitekata razvijamo sustav koji dozvojava interaktivnu tvorbu i razdiobu fleksibilne triangulirane plohe. Broj različitih sastavnih dijelova iz ekonomskih razloga treba biti mali. Zbog toga koristimo samo sukladne jednakostranične bazne trokute s mogućnošću razdiobe. Kako bismo dozvolili interaktivno kretanje vrhova i osigurali konstantnost duljine bridova umjesto inverzne kinematike koristimo metodu upravljanja silom. Rad opisuje strukturu podataka, algoritam i utjecaj razdiobe na kinematičku fleksibilnost mreže.

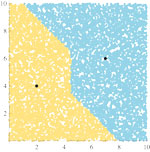
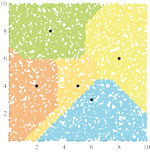
Ključne riječi: razdioba, uniformna 1-4 podjela, fleksibilni mahanizam, algoritam upravljanja silom

Članak u PDF-u.


Kristian Sabo, Sanja Scitovski (ksabo@mathos.hr, sanja@mathos.hr)

Lokacija objekata u ravnini

U radu razmatramo izravni i obratni problem lokacije objekata u ravnini uz korištenje različitih kvazimetričkih funkcija s odgovarajućim ilustracijama. Dano je nekoliko primjera iz različitih područja primjena.

Ključne riječi: grupiranje podataka, klasteri, problem lokacije, k-sredina, k-median, optimizacija

Članak u PDF-u.


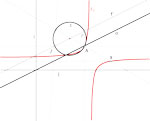
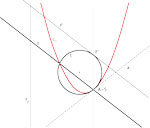
Ana Sliepčević, Ivana Božić (anas@grad.hr, ivana.bozic@tvz.hr)

Perspektivna kolineacija i oskulacijska kružnica konike u PE-ravnini i I-ravnini

Sve perspektivne kolineacije u realnoj afinoj ravnini klasificiraju se s obzirom na karakterističnu konstantu te položaj središta i osi. Pokazuje se, kako odabrati temeljne elemente perspektivne kolineacije kako bi se neka konika i njezina slika dodirivale u jednoj ili dvije točke, oskulirale se ili hiperoskulirale. Na afinim se modelima izotropne i pseudoeuklidske ravnine pomoću perspektivne kolineacije konstruiraju oskulacijske kružnice konika.

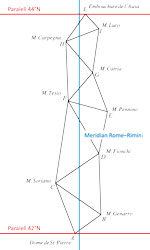
Ključne riječi: perspektivna kolineacija, homologija, elacija, karakteristična konstanta, konika, oskulacijska kružnica

Članak u PDF-u.



Martina Triplat Horvat, Miljenko Lapaine, Dražen Tutić (mthorvat@geof.hr, mlapaine@geof.hr, dtutic@geof.hr)

Primjena Boškovićeve geometrijske metode izjednačenja na pet meridijanskih stupnjeva

U ovom radu detaljno je prikazana prva metoda izjednačenja, koju je osmislio Josip Ruđer Bošković, na primjeru pet stupnjeva meridijana. Bošković je izračunao popravke kojima bi popravio duljine meridijanskih stupnjeva i na taj način dobio što bolje procjene njihovih pravih vrijednosti. Postavljajući tri uvjeta tom prilikom formirao je svoju metodu izjednačenja koju je primijenio na podatke o duljinama meridijanskih stupnjeva. Uvjeti koji moraju biti zadovoljeni objašnjeni su geometrijskom metodom kakvu Bošković opisuje u svim svojim djelima. U postupku računanja, koja su provedena u ovom radu na pet meridijanskih stupnjeva, korišteni su podaci iz Boškovićevih originalnih djela.
Geometrijsko rješenje kako ga je Bošković opisao nije odmah lako razumljivo, što su uočili i drugi autori koji su proučavali Boškovićevu metodu. Stoga će geometrijski opisana Boškovićeva metoda biti također prikazana i u analitičkom obliku.

Ključne riječi: Josip Ruđer Bošković, geometrijska metoda izjednačenja

Članak u PDF-u.


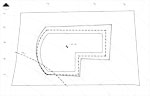
Mirela Katić Žlepalo, Boris Uremović (mkatić@tvz.hr, boris.uremovic@tvz.hr)

Primjena kotirane projekcije u određivanju obima iskopa građevinske jame

Jedan od čestih problema s kojim se građevinski inženjeri susreću tijekom planiranja procesa izgradnje je definiranje obima iskopa građevinske jame. Za rješavanje navedenog problema najčešće se koristi kotirana projekcija. U ovom članku navode se faze rješavanja obima iskopa građevinske jame i pokazuje se jedan primjer iz prakse te kako se nizom elementarnih položajnih zadataka riješenih u kotiranoj projekciji dolazi do rješenja.

Ključne riječi: kotirana projekcija, obim iskopa građevinske jame

Članak u PDF-u.