 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
| János Pallagi, Benedek Schultz, Jenö Szirmai (jpallagi@math.bme.hu, schultz.benedek@gmail.com, szirmai@math.bme.hu)
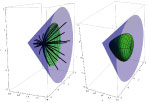
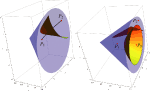
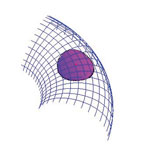
Equidistant Surfaces in H2×R SpaceAfter having investigated the equidistant surfaces ("perpendicular bisectors" of two points) in S2×R space (see[6]) we consider the analogous problem in H2×R space from among the eight Thurston geometries. In [10] the third author has determined the geodesic curves, geodesic balls of H2×R space and has computed their volume, has defined the notion of the geodesic ball packing and its density. Moreover, he has developed a procedure to determine the dendity of the geodesic ball packing for deneralized Coxeter space groups of H2×R and he has applied this algorithm to them.
 Article in PDF. Article in PDF. |
| Miljenko Lapaine (mlapaine@geof.hr)
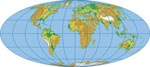
Mollweide map ProjectionKarl Brandan Mollweide (1774-1825) was German mathematician and astronomer. The formulas known after him as Mollweide's formulas are shown in the paper, as well as the proof "without words". Then, the Mollweide map projection is defined and formulas derived in different ways to show several possibilities that lead to the same result. A generalization of Mollweide projection is derived enabling to obtain a pseudocylindrical equal-area projection having the overall shape of an ellipse with any prescribed ratio of its semiaxes. The inverse equations of Mollweide projection has been derived, as well.
|
|
| Márta Szilvási-Nagy, Szilvia Béla (szilvasi@math.bme.hu, belus@math.bme.hu)
B-spline Patches Fitting on Surfaces and Triangular MeshesIn this paper a technique for the construction of quartic polynomial B-spline patches fitting on analytical surfaces and triangle meshes is presented. The input data are curvature values and principal directions at a given surface point which can be computed directly, if the surface is represented by a vector function.
|
|
| Norman John Wildberger (n.wildberger@unsw.edu.au)
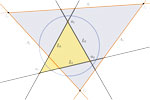
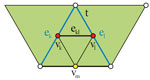
Universal Hyperbolic Geometry III: First Steps in Projective Triangle Geometry We initiate a triangle geometry in the projective metrical setting, based on the purely algebraic approach of universal geometry, and yielding in particular a new form of hyperbolic triangle geometry. There are three main strands: the Orthocenter, Incenter and Circumcenter hierarchies, with the last two dual. Formulas using ortholinear coordinates are a main objective. Prominent are five particular points, the b, z, x, h and s points, all lying on the Orthoaxis A. A rich kaleidoscopic aspect colours the subject. |
|
| Günter Wallner, Franz Gruber (guenter.wallner@uni-ak.ac.at, franz.gruber@uni-ak.ac.at)
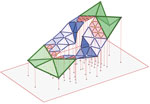
Interactive Modeling and Subdivision of Flexible Equilateral Triangular MechanismsBased on the requests from architects, we developed a system which allows to interactively design and subdivide flexible triangular surfaces. Due to economical reasons the number of different types of building elements should be small. For that reason we only use equilateral base triangles of unique size with the possibility of subdivision. To allow to interactively move vertices and to ensure constant edge length we use force-directed methods instead of inverse kinematics. This paper describes the data structure, the algorithm and the influence of subdivision on the kinematic flexibility of the mesh. |
|
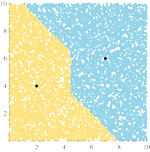
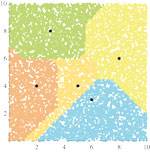
| Kristian Sabo, Sanja Scitovski (ksabo@mathos.hr, sanja@mathos.hr)
Location of Objects in a PlaneIn the paper we consider a direct and the inverse location problem in the plane. Thereby we use different distance-like functions with appropriate illustrations. Several examples from various areas of applications are given.Key words: data clustering, location problem, k-means, k-median, optimization  Article in PDF. Article in PDF. |
| Ana Sliepčević, Ivana Božić (anas@grad.hr, ivana.bozic@tvz.hr)
Perspective Collineation and Osculating Circle of Conic in PE-plane and I-planeAll perspective collineations in a real affine plane are classified according to a constant cross-ratio and the position of the center and axis. A special attention will be given to the conditions which basic elements of perspective collineation have to fulfill in order to obtain the touch or osculation or hyperosculation of two conics. On the affine models of an isotropic and pseudo - Euclidean plane the osculating circle of a conic is constructed by using perspective collineations.Key words: perspective collineation, homology, elation, constant cross - ratio, conic, osculating circle  Article in PDF. Article in PDF. |
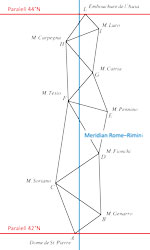
| Martina Triplat Horvat, Miljenko Lapaine, Dražen Tutić (mthorvat@geof.hr, mlapaine@geof.hr, dtutic@geof.hr)
Application of Bošković's Geometric Adjustment
|
| Mirela Katić Žlepalo, Boris Uremović (mkatić@tvz.hr, boris.uremovic@tvz.hr)
Application of Elevational Projection in Defining
|