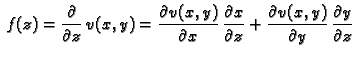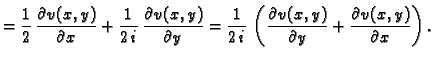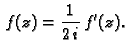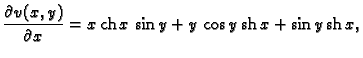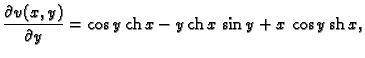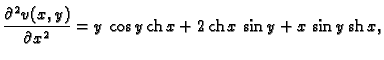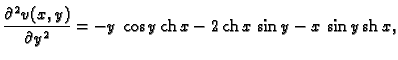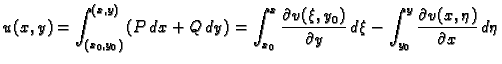Next: Integralni račun
Up: Funkcije kompleksne varijable
Previous: Elementarne funkcije
Contents
Index
Subsections
Definicija 51
Neka je

područje u
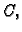
i neka je
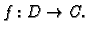
Ako

ima neprekidnu derivaciju na
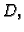
onda se takva funkcija zove
analitička funkcija.
Primjer 7.13
Odrediti područje analitičnosti funkcije
Rješenje.
Odavde se vidi da derivacija postoji i neprekidna je za svaki
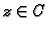
osim
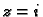
i
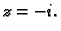
Teorem 35
1. Neka funkcija
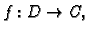
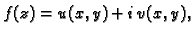
ima
neprekidnu derivaciju na
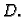
Tada su
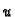
i
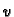
funkcije klase
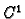
na

i za svaki
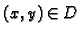
vrijede Cauchy-Riemannove jednadžbe
2. Obratno, neka su 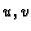 realne funkcije klase
realne funkcije klase 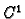 na
na 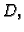 i neka vrijede
Cauchy-Riemannove jednadžbe na
i neka vrijede
Cauchy-Riemannove jednadžbe na 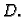 Tada funkcija
Tada funkcija  ima neprekidnu
derivaciju na
ima neprekidnu
derivaciju na 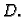
Dokaz. 1.
Ovaj limes ne ovisi o putu kojim 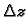 teži k nuli. Neka je
teži k nuli. Neka je
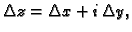 i stavimo
najprije
i stavimo
najprije
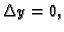 tj.
tj.
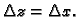 Tada
je
Sada stavimo
Tada
je
Sada stavimo
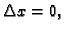 tj.
tj.
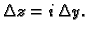 Tada je
Izjednačimo li desne strane, dobivamo upravo Cauchy-Riemannove jednadžbe.
Tada je
Izjednačimo li desne strane, dobivamo upravo Cauchy-Riemannove jednadžbe.
2. Zbog uvjeta na funkcije 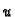 i
i 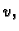 vrijede formule konačnih
prirasta
vrijede formule konačnih
prirasta
s tim da greška teži k nuli kad
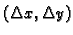 teži k
teži k
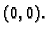
Stavimo
Tada imamo
Zbog Cauchy-Riemannovih jednadžbi
Tako je
Desna strana ne ovisi o 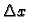 niti o
niti o
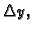 pa je
Prema tome derivacija funkcije
pa je
Prema tome derivacija funkcije  postoji. Neprekidnost parcijalnih derivacija od
postoji. Neprekidnost parcijalnih derivacija od 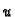 i
i 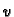 povlači neprekidnost derivacije od
povlači neprekidnost derivacije od 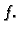

Dakle, možemo zaključiti da je funkcija  analitička na
području
analitička na
području 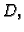 ako i samo ako njezini realni i imaginarni dijelovi
zadovoljavaju Cauchy-Riemannove jednadžbe na
ako i samo ako njezini realni i imaginarni dijelovi
zadovoljavaju Cauchy-Riemannove jednadžbe na 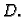
Osim toga, iz dokaza prethodnog teorema vidimo da je
odnosno, ako upotrebimo Cauchy-Riemannove jednadžbe,
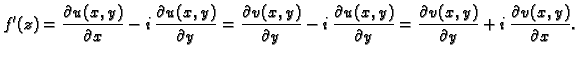 |
(7.2) |
Primjer 7.14
Nađimo derivaciju od
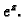
Rješenje.
Tako je
Dakle,

je analitička funkcija, i
Primjer 7.15
Nađimo derivaciju od
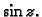
Rješenje.
Prema tome je
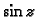
analitička funkcija, i
Na sličan način, a negdje jednostavno koristeći formule za deriviranje,
možemo dobiti da je
Harmonijske funkcije
Neka je
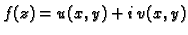 analitička funkcija. Tada vrijedi
analitička funkcija. Tada vrijedi
Derivirajmo prvu jednadžbu po 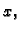 a drugu po
a drugu po 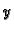 i zbrojimo. Dobivamo
Slično se može dobiti
Ova jednadžba se zove Laplaceova jednadžba. Funkcije koje
zadovoljavaju Laplaceovu jednadžbu se zovu harmonijske funkcije.
Tako imamo ovaj zaključak. Realni i imaginarni dijelovi analitičke funkcije su
harmonijske funkcije.
i zbrojimo. Dobivamo
Slično se može dobiti
Ova jednadžba se zove Laplaceova jednadžba. Funkcije koje
zadovoljavaju Laplaceovu jednadžbu se zovu harmonijske funkcije.
Tako imamo ovaj zaključak. Realni i imaginarni dijelovi analitičke funkcije su
harmonijske funkcije.
Postavlja se pitanje obrata, tj. da li se pomoću dvije harmonijske
funkcije može konstruirati analitička funkcija? Bilo koje dvije harmonijske
se ne mogu shvatiti kao realni, odnosno imaginarni dio jedne analitičke
funkcije, jer općenito neće zadovoljavati Cauchy-Riemannove
jednadžbe.
Primjer 7.16
Funkcije
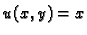
i
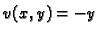
jesu harmonijske, međutim
one ne zadovoljavaju Cauchy-Riemannove jednadžbe, pa funkcija
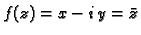
nije analitička.
Ipak vrijedi ovaj teorem.
Teorem 36
Neka je

jednostruko povezano područje, i
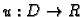
harmonijska
funkcija na
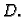
Tada postoji jedinstvena do na konstantu funkcija
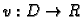
harmonijska na
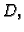
takva da je
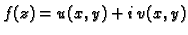
analitička funkcija.
Dokaz.
Stavimo
Odatle
pa zbog toga što 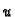 zadovoljava Laplaceovu jednadžbu, na
zadovoljava Laplaceovu jednadžbu, na  vrijedi
Taj uvjet i jednostruka povezanost područja povlače da je vektorsko polje
potencijalno (19), pa prema tome krivuljni integral druge vrste
ne ovisi o putu, već samo o krajnjim točkama. Tako možemo staviti
vrijedi
Taj uvjet i jednostruka povezanost područja povlače da je vektorsko polje
potencijalno (19), pa prema tome krivuljni integral druge vrste
ne ovisi o putu, već samo o krajnjim točkama. Tako možemo staviti
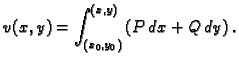 |
(7.3) |
Funkcija 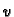 je potencijal za vektorsko polje
je potencijal za vektorsko polje
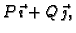 pa vrijedi
pa vrijedi
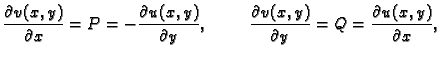 |
(7.4) |
odakle se vidi da su 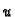 i
i 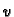 realni i imaginarni dio jedne analitičke
funkcije.
realni i imaginarni dio jedne analitičke
funkcije.
Pretpostavimo da je 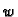 druga funkcija, takva da je
druga funkcija, takva da je 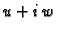 analitička
funkcija. Tada
analitička
funkcija. Tada
pa je na  Odatle slijedi da je
Odatle slijedi da je
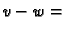 konst.
konst.

Harmonijske funkcije koje su realni odnosno imaginarni dio jedne te iste
analitičke funkcije zovu se konjugirane harmonijske funkcije.
Primjer 7.17
Naći onu analitičku funkciju
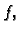
čiji je realni dio
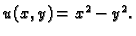
Rješenje.
Prema tome funkcija
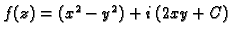
je analitička. To je jasno,
jer je
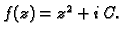
- 1.
- Kako se definira derivacija funkcije kompleksne varijable?
Navedite pravila za deriviranje.
- 2.
- Što je to analitička funkcija?
- 3.
- Navedite nužan i dovoljan uvjet da funkcija bude
analitička. Kako se ta tvrdnja dokazuje? Da li su elementarne
funkcije analitičke?
- 4.
- Pomoću kojih formula se može računati derivacija analitičke
funkcije? Napišite derivacije elementarnih funkcija.
- 5.
- Što su to harmonijske funkcije? Kakva je njihova veza s
analitičkim funkcijama?
- 6.
- Kada dvije harmonijske funkcije zovemo konjugiranima? Da li bilo
koje dvije harmonijske funkcije tvore analitičku funkciju? Dajte
primjer. Kako se iz harmonijske funkcije dobiva analitička?
- 1.
- Derivirati funkciju
i navesti u kojim točkama
 nije derivabilna.
nije derivabilna.
Rješenje. Derivacija je
pa funkcija nije derivabilna u točkama za koje je
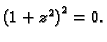 To su točke
To su točke 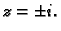
- 2.
- Provjeriti da su Cauchy-Riemannove jednadžbe ekvivalentne
jednadžbi
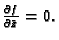
Rješenje. Neka je
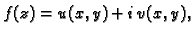 i
i 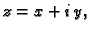 odnosno
odnosno
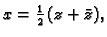
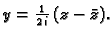
Imamo
Kad ovo uvrstimo gore, sredimo i izjednačimo s nulom, dobivamo upravo
Iz ove formule slijedi tražena ekvivalencija.
- 3.
- Neka je
 analitička funkcija. Tada vrijedi
analitička funkcija. Tada vrijedi
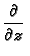
Im
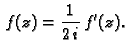
Rješenje. Neka je
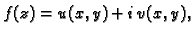 i
i 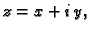 odnosno
odnosno
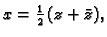
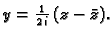
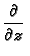
Im
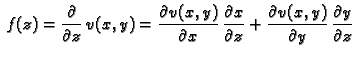
Iz formule (7.2) slijedi
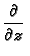
Im
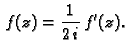
- 4.
- Naći analitičku funkciju
 ako je
ako je
Im
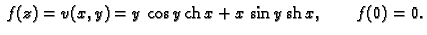
Rješenje. Najprije treba provjeriti da li je dana funkcija harmonijska.
pa je očito
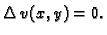
Analogno formulama (7.3) i (7.4)
imamo
Iz uvjeta 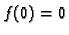 slijedi
slijedi





Next: Integralni račun
Up: Funkcije kompleksne varijable
Previous: Elementarne funkcije
Contents
Index
Salih Suljagic
2000-03-11
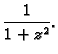
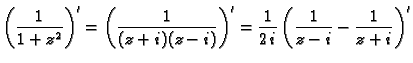
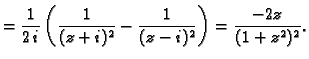
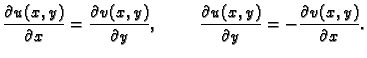
![]() realne funkcije klase
realne funkcije klase ![]() na
na ![]() i neka vrijede
Cauchy-Riemannove jednadžbe na
i neka vrijede
Cauchy-Riemannove jednadžbe na ![]() Tada funkcija
Tada funkcija ![]() ima neprekidnu
derivaciju na
ima neprekidnu
derivaciju na ![]()
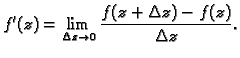
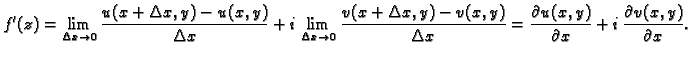
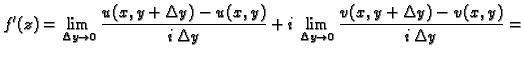
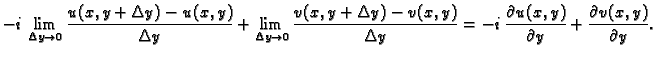
![]() i
i ![]() vrijede formule konačnih
prirasta
vrijede formule konačnih
prirasta
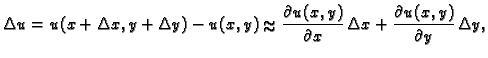
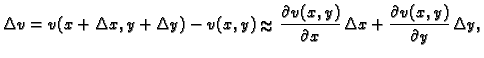
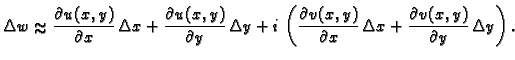
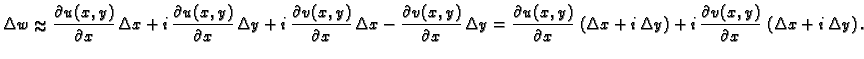
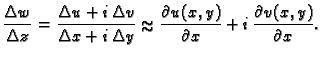
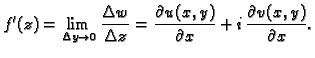
![]() analitička na
području
analitička na
području ![]() ako i samo ako njezini realni i imaginarni dijelovi
zadovoljavaju Cauchy-Riemannove jednadžbe na
ako i samo ako njezini realni i imaginarni dijelovi
zadovoljavaju Cauchy-Riemannove jednadžbe na ![]()
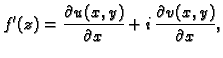
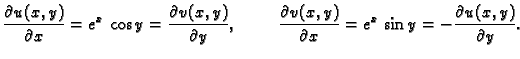
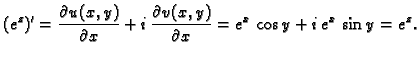
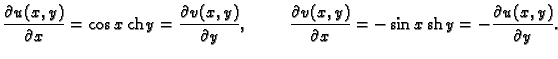
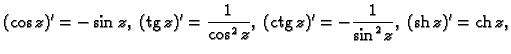
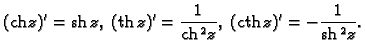
![]() analitička funkcija. Tada vrijedi
analitička funkcija. Tada vrijedi
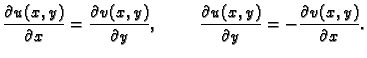
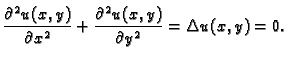
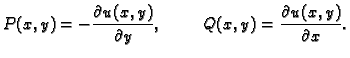
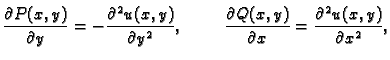
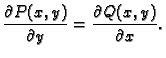
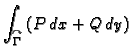
![]() druga funkcija, takva da je
druga funkcija, takva da je ![]() analitička
funkcija. Tada
analitička
funkcija. Tada
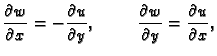
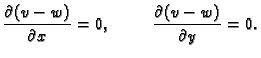
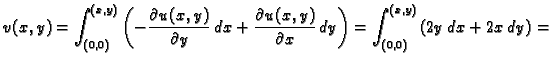
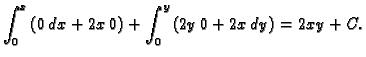
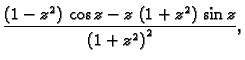
![]() i
i ![]() odnosno
odnosno
![]()
![]()
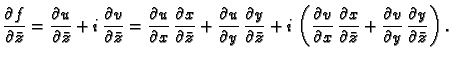
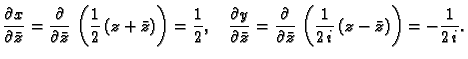
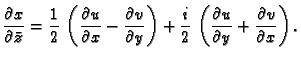
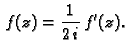
![]() i
i ![]() odnosno
odnosno
![]()
![]()