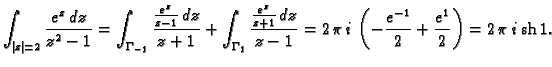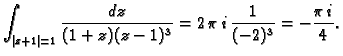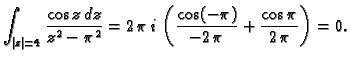Next: Konformno preslikavanje i primjene
Up: Funkcije kompleksne varijable
Previous: Analitičke i harmonijske funkcije
Contents
Index
Subsections
Neka je
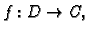 gdje je
gdje je  područje u
područje u 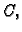 neprekidna
funkcija na
neprekidna
funkcija na 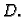 Neka je
Neka je
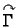 glatka
orijentirana krivulja u
glatka
orijentirana krivulja u 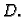 Neka je
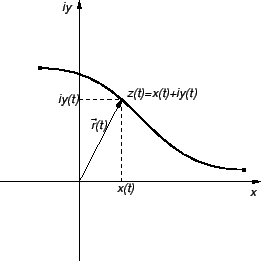
Neka je
![$ \vec{r}\,(t)=x(t)\,\vec{\imath}+y(t)\,\vec{\jmath},\;t\in [a,b],$](img3548.gif) njezina
parametrizacija. Točke na krivulji tada možemo pisati kao
njezina
parametrizacija. Točke na krivulji tada možemo pisati kao
Tada je
pa je
što
se može kraće zapisati kao
ako se uzme u obzir da je
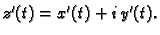
Ako je krivulja  po dijelovima glatka, onda se integral definira kao
suma integrala po glatkim dijelovima. Ovdje se radi ustvari o krivuljnom
integralu druge vrste, pa prema tome integral ovisi o orijentaciji krivulje.
po dijelovima glatka, onda se integral definira kao
suma integrala po glatkim dijelovima. Ovdje se radi ustvari o krivuljnom
integralu druge vrste, pa prema tome integral ovisi o orijentaciji krivulje.
Navedimo neka svojstva integrala.
- 1.
- Za proizvoljne kompleksne brojeve
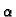 i
i 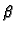 i neprekidne
funkcije
i neprekidne
funkcije  i
i 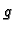 na
na  vrijedi
vrijedi
- 2.
- Ako je
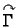 krivulja sastavljena od dvije krivulje
krivulja sastavljena od dvije krivulje
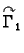 i
i
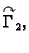 onda vrijedi
onda vrijedi
- 3.
- Neka je
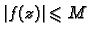 za
za
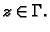 Tada vrijedi
gdje je
Tada vrijedi
gdje je
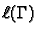 duljina krivulje
duljina krivulje 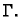
Primjer 7.18
Izračunati
po kružnici oko
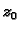
radiusa
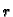
pozitivno orijentiranoj (protivno
kretanju kazaljke na satu).
Rješenje. Jednadžba kružnice je
i pritom ova parametrizacija daje pozitivnu orijentaciju. Odatle
pa je
Uočite da integral
ne ovisi o 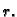
Primjer 7.19
Izračunati
po istoj kružnici kao u prethodnom primjeru.
Rješenje.
jer je
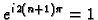
za proizvoljan cijeli broj
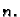
Uočite da niti ovaj integral
ne ovisi o 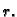
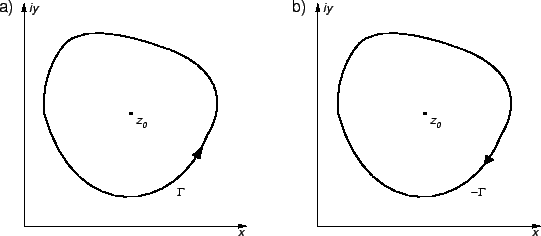
Slika 7.4:
a) Pozitivno orijentirana krivulja. Točka 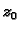 se nalazi u unutrašnjem području. b) Negativno orijentirana krivulja. Točka
se nalazi u unutrašnjem području. b) Negativno orijentirana krivulja. Točka 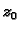 se ne nalazi u unutrašnjem području.
se ne nalazi u unutrašnjem području.
|
|
U daljnjem ćemo često zahtijevati da krivulja  bude
zatvorena. U tom slučaju kažemo da je
bude
zatvorena. U tom slučaju kažemo da je  pozitivno orijentirana ako orijentacija
nalaže obilaženje po krivulji protivno kazaljci na satu. Suprotnu
orijentaciju, tj. u smjeru kazaljke na satu, zvat ćemo
negativnom orijentacijom zatvorene krivulje
pozitivno orijentirana ako orijentacija
nalaže obilaženje po krivulji protivno kazaljci na satu. Suprotnu
orijentaciju, tj. u smjeru kazaljke na satu, zvat ćemo
negativnom orijentacijom zatvorene krivulje
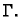 Unutrašnjim područjem orijentirane krivulje
Unutrašnjim područjem orijentirane krivulje
 smatrat ćemo onaj dio kompleksne ravnine koji ostaje s
lijeve strane prilikom obilaska po krivulji u smjeru
orijentacije. Također ćemo reći da orijentirana krivulja
smatrat ćemo onaj dio kompleksne ravnine koji ostaje s
lijeve strane prilikom obilaska po krivulji u smjeru
orijentacije. Također ćemo reći da orijentirana krivulja  obuhvaća točku
obuhvaća točku 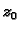 , ako se točka
, ako se točka 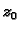 nalazi u njezinom
unutrašnjem području. Kad se radi o zatvorenoj krivulji, oznaka
nalazi u njezinom
unutrašnjem području. Kad se radi o zatvorenoj krivulji, oznaka
 će značiti automatski pozitivnu orijentiranost. Negativno
orijentiranu krivulju ćemo označavati s
će značiti automatski pozitivnu orijentiranost. Negativno
orijentiranu krivulju ćemo označavati s
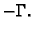
Teorem 37
Neka je

analitička funkcija na jednostruko povezanom području
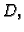
i neka je

zatvorena, po dijelovima glatka krivulja u
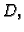
orijentirana tako da se unutrašnje područje od

nalazi u

(v. sl.
7.5). Tada je
Slika 7.5:
Integral po  funkcije, analitičke na
funkcije, analitičke na  iščezava.
iščezava.
|
|
Dokaz. Iz analitičnosti funkcije
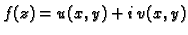 slijedi da
slijedi da 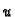 i
i 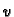 zadovoljavaju Cauchy-Riemannove
jednadžbe
zadovoljavaju Cauchy-Riemannove
jednadžbe
To znači da su vektorska polja
konzervativna, pa njihovi krivuljni integrali druge vrste po zatvorenoj
krivulji iščezavaju.
Tako je
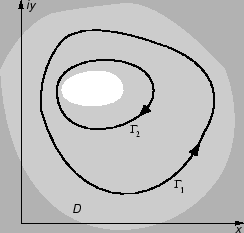
Posljedica. Neka je  višestruko povezano područje i neka je
višestruko povezano područje i neka je
 analitička na
analitička na 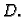 Neka su u
Neka su u  dane po dijelovima glatke, zatvorene
krivulje
dane po dijelovima glatke, zatvorene
krivulje 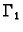 i
i 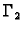 koje se međusobno ne sijeku, tako da
je
koje se međusobno ne sijeku, tako da
je
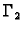 u unutrašnjem području krivulje
u unutrašnjem području krivulje
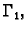 i da
presjek unutrašnjih područja
i da
presjek unutrašnjih područja
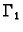 i
i
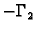 leži u
leži u
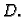
Tada vrijedi
gdje je
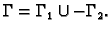
Primjedba. Neka je  područje,
područje,  funkcija analitička na
funkcija analitička na
 osim možda u točki
osim možda u točki 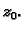 Odaberimo u
Odaberimo u  zatvorenu, po
dijelovima glatku pozitivno orijentiranu krivulju
zatvorenu, po
dijelovima glatku pozitivno orijentiranu krivulju  unutar koje
se nalazi
unutar koje
se nalazi 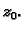 Opišimo oko
Opišimo oko 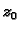 pozitivno orijentiranu kružnicu
pozitivno orijentiranu kružnicu
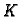 tako da potpuno leži u unutrašnjem području krivulje
tako da potpuno leži u unutrašnjem području krivulje
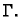 Na području omeđenom krivuljom
Na području omeđenom krivuljom  i kružnicom
i kružnicom 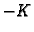 funkcija
funkcija  je analitička. Tako je
je analitička. Tako je
Odatle je
Isti zaključak dobivamo i ako se  nalazi u unutrašnjem
području kružnice. Tako možemo, ako su ispunjeni gornji uvjeti,
integral analitičke funkcije po bilo kakvoj krivulji zamijeniti
integralom po kružnici.
nalazi u unutrašnjem
području kružnice. Tako možemo, ako su ispunjeni gornji uvjeti,
integral analitičke funkcije po bilo kakvoj krivulji zamijeniti
integralom po kružnici.
Teorem 38
Neka je

analitička funkcija na jednostruko povezanom području
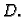
Tada
integral
ne ovisi o putu integracije, već samo o krajnjim točkama. Funkcija
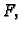
koju on određuje, je analitička, i vrijedi
Dokaz. Da integral ne ovisi o putu slijedi odmah
iz Cauchyjevog teorema. Analitičnost od 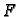 će slijediti, ako dokažemo
da je
će slijediti, ako dokažemo
da je
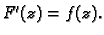
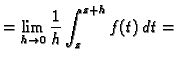
prema teoremu srednje vrijednosti za integrale
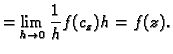

Funkcija 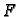 se zove primitivna funkcija funkcije
se zove primitivna funkcija funkcije 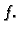
Teorem 39
Neka je

jednostruko povezano područje i neka je
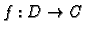
analitička funkcija na
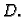
Neka je

po dijelovima glatka zatvorena krivulja u
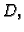
orijentirana tako da
unutrašnje područje od

leži u

(v. sl.
7.5). Tada za svaki
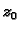
u unutrašnjem području od

vrijedi
Dokaz. Neka je
Funkcija 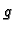 nije definirana u
nije definirana u 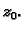 No
No
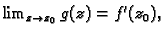 pa ako stavimo
pa ako stavimo
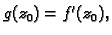 onda je tako proširena funkcija
onda je tako proširena funkcija 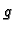 neprekidna na
neprekidna na 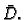 Osim toga
funkcija
Osim toga
funkcija 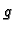 je analitička u
je analitička u  osim u točki
osim u točki 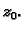 Prema tome
za bilo koji
Prema tome
za bilo koji 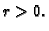 To znači da drugi integral ne ovisi o
To znači da drugi integral ne ovisi o 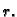 No, funkcija
No, funkcija
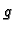 je neprekidna na kružnici
je neprekidna na kružnici
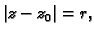 kružnica je zatvoren ograničen
skup, pa postoji
kružnica je zatvoren ograničen
skup, pa postoji 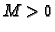 takav da je
takav da je
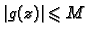 za svaki
za svaki 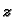 na kružnici.
Prema svojstvu integrala
Budući da integral ne ovisi o
na kružnici.
Prema svojstvu integrala
Budući da integral ne ovisi o 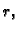 i da se on može uzeti po volji malen,
slijedi
Odatle
tj.
što je formula iz teorema drugačije napisana.
i da se on može uzeti po volji malen,
slijedi
Odatle
tj.
što je formula iz teorema drugačije napisana.

Formula
se zove Cauchyjeva formula. Ona vrijedi i u slučaju višestruko
povezanog područja 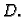
Primjer 7.20
Izračunati integral
gdje je

zatvorena glatka krivulja koja obuhvaća točku
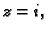
ali
ne obuhvaća točku
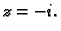
Rješenje.
Primjer 7.21
Izračunati
gdje je

pozitivno orijentirana središnja kružnica radiusa
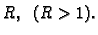
Rješenje. Funkcija
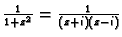 nije analitička u krugu
omeđenom kružnicom
nije analitička u krugu
omeđenom kružnicom 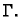 No, ako opišemo kružnice
No, ako opišemo kružnice 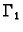 i
i
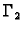 radiusa
radiusa 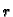 oko
oko 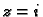 i oko
i oko 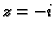 tako da potpuno leže unutar
tako da potpuno leže unutar 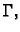 onda u
području između ovih kružnica i kružnice
onda u
području između ovih kružnica i kružnice  funkcija
funkcija
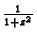 jeste analitička. Ako kružnice
jeste analitička. Ako kružnice 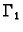 i
i
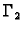 pozitivno orijentiramo, onda po Cauchyjevom teoremu za
višestruko povezana područja
pozitivno orijentiramo, onda po Cauchyjevom teoremu za
višestruko povezana područja
Tako je
Na kraju napomenimo da funkcija
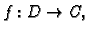 analitička na
području
analitička na
području 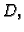 ima na
ima na  derivaciju bilo kojeg reda, i ona se u
točki
derivaciju bilo kojeg reda, i ona se u
točki 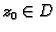 računa po formuli
računa po formuli
gdje je  bilo koja
zatvorena, po dijelovima glatka, pozitivno orijentirana krivulja u
bilo koja
zatvorena, po dijelovima glatka, pozitivno orijentirana krivulja u 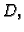 koja obuhvaća točku
koja obuhvaća točku 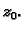
- 1.
- Kako se definira integral funkcije kompleksne varijable? O kojem
se integralu ovdje radi?
- 2.
- Kakvu orijentaciju zatvorene krivulje smatramo pozitivnom, a
kakvu negativnom? Što je unutrašnje područje zatvorene
orijentirane krivulje?
- 3.
- Kako glasi Cauchyjev teorem? Da li ga znate dokazati?
- 4.
- Kad kažemo da je neko područje višestruko povezano? Da li
Cauchyjev teorem vrijedi za višestruko povezana područja?
- 5.
- Što je primitivna funkcija neke analitičke funkcije? Kako se
može izračunati? Zašto?
- 6.
- Kako glasi Cauchyjeva formula?
- 7.
- Koje važno svojstvo imaju analitičke funkcije?
- 1.
- Izračunati
po pravcu od točke
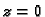 do točke
do točke 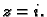
Rješenje. Parametrizacija krivulje integracije je
![$ z=i\,t,\;t\in [0,1].$](img3622.gif) Slijedi
Slijedi
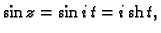
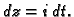 Dakle
Dakle
- 2.
- Pomoću Cauchyjeve formule izračunati sljedeće integrale
Kružnice po kojima se integrira su pozitivno orijentirane.
Rješenje. a) U unutrašnjem području krivulje nalaze se dvije točke u
kojima finkcija nije analitička 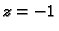 i
i 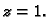 Prema primjeru
7.21 integral je jednak sumi integrala oko ovih
točaka po pozitivno orijentiranim kručnicama koje obilaze samo jednu od
njih. Dakle
Prema primjeru
7.21 integral je jednak sumi integrala oko ovih
točaka po pozitivno orijentiranim kručnicama koje obilaze samo jednu od
njih. Dakle
b) Točke u kojima funkcija nije analitička su 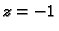 i
i 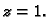 U
unutrašnjem području se nalazi samo točka
U
unutrašnjem području se nalazi samo točka 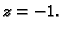 Tako imamo
c) Točke u kojima funkcija nije analitička jesu
Tako imamo
c) Točke u kojima funkcija nije analitička jesu 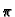 i
i 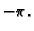 Obje
leže u unutrašnjem području kružnice, pa imamo
Obje
leže u unutrašnjem području kružnice, pa imamo





Next: Konformno preslikavanje i primjene
Up: Funkcije kompleksne varijable
Previous: Analitičke i harmonijske funkcije
Contents
Index
Salih Suljagic
2000-03-11
![]() gdje je
gdje je ![]() područje u
područje u ![]() neprekidna
funkcija na
neprekidna
funkcija na ![]() Neka je
Neka je
![]() glatka
orijentirana krivulja u
glatka
orijentirana krivulja u ![]() Neka je
Neka je
![]() njezina
parametrizacija. Točke na krivulji tada možemo pisati kao
njezina
parametrizacija. Točke na krivulji tada možemo pisati kao
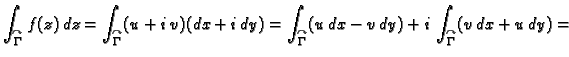
![$\displaystyle \int_a^b\left[u(x(t),y(t))x'(t)-v(x(t),y(t))y'(t)\right]dt +
i\,\int_a^b\left[v(x(t),y(t))x'(t)+u(x(t),y(t))y'(t)\right]dt,$](img3553.gif)
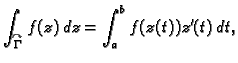
![]() po dijelovima glatka, onda se integral definira kao
suma integrala po glatkim dijelovima. Ovdje se radi ustvari o krivuljnom
integralu druge vrste, pa prema tome integral ovisi o orijentaciji krivulje.
po dijelovima glatka, onda se integral definira kao
suma integrala po glatkim dijelovima. Ovdje se radi ustvari o krivuljnom
integralu druge vrste, pa prema tome integral ovisi o orijentaciji krivulje.
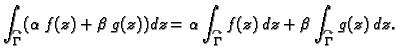
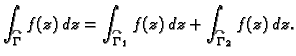
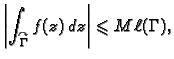
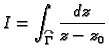
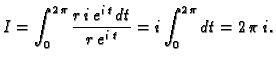
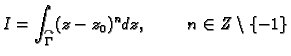
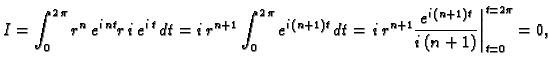
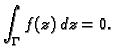
![]() slijedi da
slijedi da ![]() i
i ![]() zadovoljavaju Cauchy-Riemannove
jednadžbe
zadovoljavaju Cauchy-Riemannove
jednadžbe
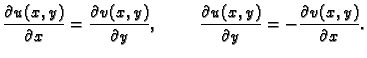
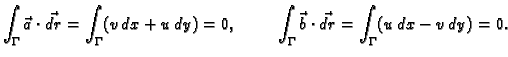
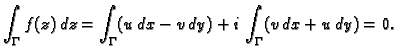
![]() višestruko povezano područje i neka je
višestruko povezano područje i neka je
![]() analitička na
analitička na ![]() Neka su u
Neka su u ![]() dane po dijelovima glatke, zatvorene
krivulje
dane po dijelovima glatke, zatvorene
krivulje ![]() i
i ![]() koje se međusobno ne sijeku, tako da
je
koje se međusobno ne sijeku, tako da
je
![]() u unutrašnjem području krivulje
u unutrašnjem području krivulje
![]() i da
presjek unutrašnjih područja
i da
presjek unutrašnjih područja
![]() i
i
![]() leži u
leži u
![]()
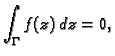
![]() područje,
područje, ![]() funkcija analitička na
funkcija analitička na
![]() osim možda u točki
osim možda u točki ![]() Odaberimo u
Odaberimo u ![]() zatvorenu, po
dijelovima glatku pozitivno orijentiranu krivulju
zatvorenu, po
dijelovima glatku pozitivno orijentiranu krivulju ![]() unutar koje
se nalazi
unutar koje
se nalazi ![]() Opišimo oko
Opišimo oko ![]() pozitivno orijentiranu kružnicu
pozitivno orijentiranu kružnicu
![]() tako da potpuno leži u unutrašnjem području krivulje
tako da potpuno leži u unutrašnjem području krivulje
![]() Na području omeđenom krivuljom
Na području omeđenom krivuljom ![]() i kružnicom
i kružnicom ![]() funkcija
funkcija ![]() je analitička. Tako je
je analitička. Tako je
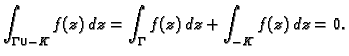
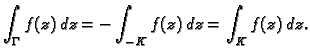
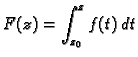
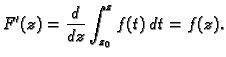
![]() će slijediti, ako dokažemo
da je
će slijediti, ako dokažemo
da je
![]()
![$\displaystyle F'(z)=\lim_{h \rightarrow 0} \frac{1}{h}[F(z+h)-F(z)]=
\lim_{h \r...
...ow 0}
\frac{1}{h}\left[\int_{z_0}^{z+h} f(t)\,dt-\int_{z_0}^z f(t)\,dt\right]=$](img3590.gif)
![$\displaystyle =\lim_{h \rightarrow 0}
\frac{1}{h}\left[\int_{z_0}^{z+h} f(t)\,dt+\int_z^{z_0} f(t)\,dt\right]=$](img3591.gif)
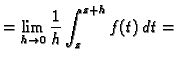 prema teoremu srednje vrijednosti za integrale
prema teoremu srednje vrijednosti za integrale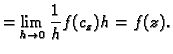
![]() se zove primitivna funkcija funkcije
se zove primitivna funkcija funkcije ![]()
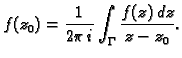
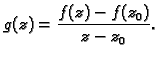
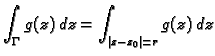
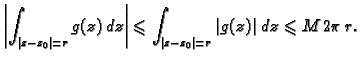
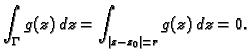
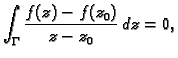
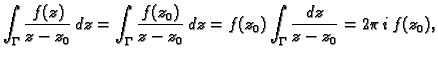
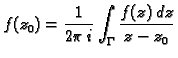
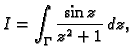
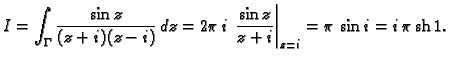
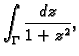
![]() nije analitička u krugu
omeđenom kružnicom
nije analitička u krugu
omeđenom kružnicom ![]() No, ako opišemo kružnice
No, ako opišemo kružnice ![]() i
i
![]() radiusa
radiusa ![]() oko
oko ![]() i oko
i oko ![]() tako da potpuno leže unutar
tako da potpuno leže unutar ![]() onda u
području između ovih kružnica i kružnice
onda u
području između ovih kružnica i kružnice ![]() funkcija
funkcija
![]() jeste analitička. Ako kružnice
jeste analitička. Ako kružnice ![]() i
i
![]() pozitivno orijentiramo, onda po Cauchyjevom teoremu za
višestruko povezana područja
pozitivno orijentiramo, onda po Cauchyjevom teoremu za
višestruko povezana područja
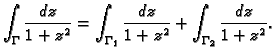
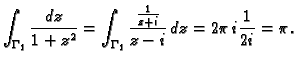
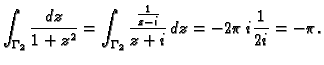
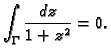
![]() analitička na
području
analitička na
području ![]() ima na
ima na ![]() derivaciju bilo kojeg reda, i ona se u
točki
derivaciju bilo kojeg reda, i ona se u
točki ![]() računa po formuli
računa po formuli
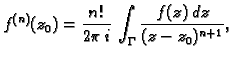
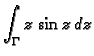
![]() Slijedi
Slijedi
![]()
![]() Dakle
Dakle
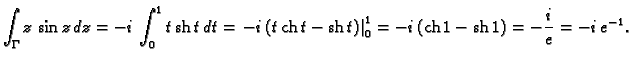
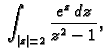 b)
b)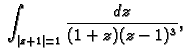 c)
c)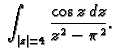
![]() i
i ![]() Prema primjeru
7.21 integral je jednak sumi integrala oko ovih
točaka po pozitivno orijentiranim kručnicama koje obilaze samo jednu od
njih. Dakle
Prema primjeru
7.21 integral je jednak sumi integrala oko ovih
točaka po pozitivno orijentiranim kručnicama koje obilaze samo jednu od
njih. Dakle