




Next: Dodaci
Up: Funkcije kompleksne varijable
Previous: Integralni račun
Contents
Index
Subsections
Neka je  područje u
područje u 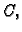 neka je
neka je
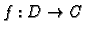 analitička
funkcija, neka je
analitička
funkcija, neka je 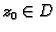 i neka je
i neka je
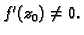 Budući da je
analitička, funkcija
Budući da je
analitička, funkcija  ima derivacije bilo kojeg reda. To znači da
za proizvoljan
ima derivacije bilo kojeg reda. To znači da
za proizvoljan 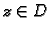 postoji
postoji
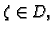 koji se nalazi na
spojnici točaka
koji se nalazi na
spojnici točaka 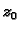 i
i 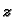 tako da vrijedi
tako da vrijedi
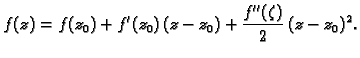 |
(7.5) |
Za
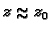 je
je
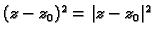 vrlo maleno, pa član
vrlo maleno, pa član
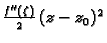 vrlo malo utječe na ponašanje
funkcije
vrlo malo utječe na ponašanje
funkcije  (kvadrat malenog pozitivnog broja je puno manji od samog
broja). Zaključujemo da se funkcija
(kvadrat malenog pozitivnog broja je puno manji od samog
broja). Zaključujemo da se funkcija  lokalno u točki
lokalno u točki 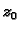 ponaša kao funkcija
Preslikavanje
ponaša kao funkcija
Preslikavanje 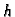 je složeno od
translacije za
je složeno od
translacije za 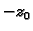 i preslikavanja opisanog u primjeru
7.2. Ovo posljednje je kompozicija homotetije
(rotacije za kut
i preslikavanja opisanog u primjeru
7.2. Ovo posljednje je kompozicija homotetije
(rotacije za kut
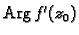 i rastezanja ili stezanja za faktor
i rastezanja ili stezanja za faktor
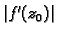 ), i translacije za
), i translacije za 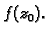 Prema tome to preslikavanje
čuva kuteve, i kružnice oko
Prema tome to preslikavanje
čuva kuteve, i kružnice oko 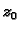 preslikava u kružnice oko
preslikava u kružnice oko
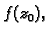 s tim da se radius može pri tom povećati ili smanjiti.
Preslikavanje, koje lokalno ima ta svojstva u svakoj točki nekog
područja
s tim da se radius može pri tom povećati ili smanjiti.
Preslikavanje, koje lokalno ima ta svojstva u svakoj točki nekog
područja  u kompleksnoj ravnini, zove se konformno
preslikavanje.
u kompleksnoj ravnini, zove se konformno
preslikavanje.
Dakle, ako je  analitička funkcija na području
analitička funkcija na području  u kompleksnoj
ravnini, i
u kompleksnoj
ravnini, i
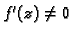 za svaki
za svaki 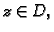 onda je funkcijom
onda je funkcijom  definirano konformno preslikavanje područja
definirano konformno preslikavanje područja  u
u 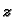 -ravnini u
njegovu
-ravnini u
njegovu  -sliku, područje
-sliku, područje 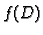 u
u 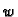 -ravnini. Vrijedi i obrat. Ako je
preslikavanje područja
-ravnini. Vrijedi i obrat. Ako je
preslikavanje područja  u
u 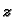 -ravnini u područje
-ravnini u područje 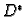 u
u
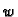 -ravnini konformno, onda postoji analitička funkcija
-ravnini konformno, onda postoji analitička funkcija  na
na  takva da je
takva da je
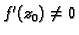 i da preslikava
i da preslikava  na
na 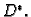
Osnovni problem se sastoji u tome da se za zadana područja  i
i
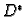 nađe funkcija koja ostvaruje konformno preslikavanje
područja
nađe funkcija koja ostvaruje konformno preslikavanje
područja  na područje
na područje 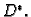
Teorem 40
(Riemann)
Neka su

i
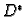
proizvoljna jednostruko povezana područja
takva da im granice sadrže više od jedne točke, i neka su dani
proizvoljni
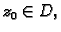
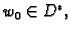
i realan broj
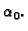
Slika 7.6:
Konformno preslikavanje.
|
|
Tada postoji jedno i samo jedno konformno preslikavanje
područja

na područje
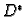
takvo da je
Razlomljeno linearno preslikavanje
Funkcija zadana s kompleksnim brojevima 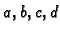 formulom
formulom
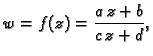
gdje je
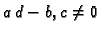
se zove razlomljeno linearno preslikavanje, ili
razlomljeno linearna funkcija.
Domena razlomljeno linearnog preslikavanja je
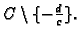 Derivacija je
Derivacija je
pa se vidi da uvjet na koeficijente 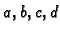 osigurava konformnost
razlomljeno linearnog preslikavanja.
osigurava konformnost
razlomljeno linearnog preslikavanja.
Budući da se brojnik i nazivnik mogu podijeliti s onim od brojeva
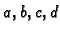 koji je različit od nule, vidimo da je razlomljeno linearno
preslikavanje zadano s tri uvjeta. Tako zahtjev da određene tri
točke
koji je različit od nule, vidimo da je razlomljeno linearno
preslikavanje zadano s tri uvjeta. Tako zahtjev da određene tri
točke 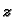 -ravnine budu preslikane u određene tri točke
-ravnine budu preslikane u određene tri točke 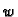 -ravnine
potpuno određuje razlomljeno linearno preslikavanje. Razlomljeno
linearno preslikavanje je injekcija, tj. ne lijepi točke, i preslikava
pravce i kružnice u pravce i kružnice.
-ravnine
potpuno određuje razlomljeno linearno preslikavanje. Razlomljeno
linearno preslikavanje je injekcija, tj. ne lijepi točke, i preslikava
pravce i kružnice u pravce i kružnice.
Primjer 7.22
Odrediti ono razlomljeno linearno preslikavanje koje preslikava
točke
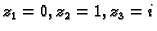
redom u točke
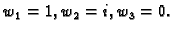
Slika 7.7:
Linearno razlomljeno preslikavanje.
|
|
Rješenje. Iz uvjeta
slijedi
Traženo preslikavanje je dakle
Da bismo vidjeli u što se preslikava realna os, nađimo sliku još
jedne, treće točke na realnoj osi. Za 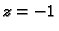 imamo
imamo
Dakle, točke
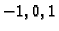
se preslikavaju u
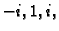
pa slijedi da se
realna os preslikava u jediničnu kružnicu. Osim toga
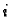
se
preslikava u
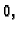
pa se prema tome gornja poluravnina preslikava u
jedinični krug.
Dirichletov problem
Neka je dano područje 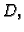 i neka je dana neprekidna funkcija
i neka je dana neprekidna funkcija 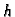 na
rubu
na
rubu
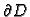 područja
područja 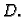 Treba naći funkciju
Treba naći funkciju 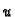 harmonijsku
na području
harmonijsku
na području 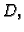 neprekidnu na rubu
neprekidnu na rubu
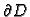 takvu da je
takvu da je
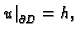 tj. treba riješiti problem
tj. treba riješiti problem
Kad se radi o jediničnom krugu kao području, Dirichletov problem
rješava Poissonov integral. Ako je 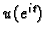 neprekidna funkcija na
jediničnoj kružnici, onda je funkcija
neprekidna funkcija na
jediničnoj kružnici, onda je funkcija
harmonijska u unutrašnjosti jediničnog kruga, neprekidna na
jediničnoj kružnici, i prima vrijednosti 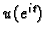 na njoj.
na njoj.
Neka je  proizvoljno jednostruko povezano područje čiji rub
sadrži više od jedne točke, i neka je na njegovom rubu
proizvoljno jednostruko povezano područje čiji rub
sadrži više od jedne točke, i neka je na njegovom rubu
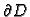 zadana neprekidna funkcija
zadana neprekidna funkcija 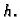 Prema Riemannovom
teoremu postoji konformno preslikavanje
Prema Riemannovom
teoremu postoji konformno preslikavanje  sa
sa  na jedinični krug.
Funkcija
na jedinični krug.
Funkcija  preslikava
preslikava 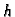 u funkciju
u funkciju
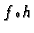 neprekidnu na
jediničnoj kružnici. Ako sada primijenimo Poissonov integral na
funkciju
neprekidnu na
jediničnoj kružnici. Ako sada primijenimo Poissonov integral na
funkciju
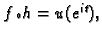 dobit ćemo harmonijsku funkciju
dobit ćemo harmonijsku funkciju 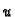 u
jediničnom krugu, koja se na jediničnoj kružnici poklapa s
u
jediničnom krugu, koja se na jediničnoj kružnici poklapa s
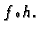 Kompozicija
Kompozicija
je harmonijska funkcija na  takva da se na rubu
takva da se na rubu
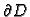 od
od
 poklapa s
poklapa s 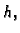 dakle rješenje Dirichletovog problema za područje
dakle rješenje Dirichletovog problema za područje
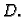
Razmotrimo stacionarno, bezvrtložno, ravninsko gibanje nestlačivog fluida u jednostruko povezanom području 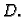 Jednadžba kontinuiteta
Jednadžba kontinuiteta
u tom slučaju glasi
Bezvrtložnost se izražava jednadžbom
Pretpostavimo da je polje brzina
Tada gornje jednadžbe daju
To su Cauchy-Riemannove jednadžbe za funkcije 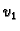 i
i 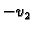 . Slijedi
da je
analitička funkcija. Funkcija
. Slijedi
da je
analitička funkcija. Funkcija 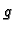 se zove kompleksna brzina.
se zove kompleksna brzina.
Osim toga
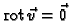 na
na  znači da je vektorsko
polje brzina potencijalno, tj. da postoji skalarno polje (potencijal
brzine)
znači da je vektorsko
polje brzina potencijalno, tj. da postoji skalarno polje (potencijal
brzine) 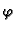 na
na 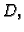 takvo da je
takvo da je
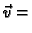
grad
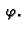
Odatle
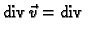
grad
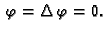
Tako je 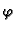 harmonijska funkcija na
harmonijska funkcija na 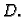 Neka je
Neka je 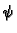 konjugirana
harmonijska funkcija. Tada je
analitička funkcija. Ona se zove kompleksni potencijal. Funkcija
konjugirana
harmonijska funkcija. Tada je
analitička funkcija. Ona se zove kompleksni potencijal. Funkcija
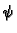 ima svojstvo da je konstantna na strujnicama (linijama toka) fluida.
Zato se zove funkcija toka. Kad nju znamo, onda nam njezine
nivokrivulje daju strujnice. S druge strane, nivokrivulje funkcije
ima svojstvo da je konstantna na strujnicama (linijama toka) fluida.
Zato se zove funkcija toka. Kad nju znamo, onda nam njezine
nivokrivulje daju strujnice. S druge strane, nivokrivulje funkcije
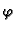 nam daju linije istog potencijala brzine. I jedna i druga
funkcija se pojavljuju kao rješenja Laplaceove jednadžbe.
nam daju linije istog potencijala brzine. I jedna i druga
funkcija se pojavljuju kao rješenja Laplaceove jednadžbe.
U teoriji elastičnosti prilikom analize deformacija čvrstog tijela u
ravnini, dolazi se do Maxwellove jednadžbe
Pomoću funkcije 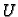 se mogu dobro opisati
naprezanja kojima je podvrgnuto tijelo i njegovi pomaci. Funkcije, koje rješavaju
Maxwellovu jednadžbu, se zovu biharmonijske funkcije. Važnost
funkcija kompleksne varijable u rješavanju problema elastičnosti ogleda
se u činjenici da se i biharmonijske funkcije mogu opisati pomoću
analitičkih funkcija.
se mogu dobro opisati
naprezanja kojima je podvrgnuto tijelo i njegovi pomaci. Funkcije, koje rješavaju
Maxwellovu jednadžbu, se zovu biharmonijske funkcije. Važnost
funkcija kompleksne varijable u rješavanju problema elastičnosti ogleda
se u činjenici da se i biharmonijske funkcije mogu opisati pomoću
analitičkih funkcija.
Neka je 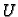 proizvoljna biharmonijska funkcija. Tada je
proizvoljna biharmonijska funkcija. Tada je 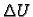 harmonijska, pa postoji analitička funkcija
harmonijska, pa postoji analitička funkcija  takva da je
takva da je
Umjesto funkcije  pogodnije je promatrati četvrtinu njezine primitivne.
Funkcija
pogodnije je promatrati četvrtinu njezine primitivne.
Funkcija 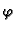 je također analitička, pa su
je također analitička, pa su 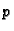 i
i 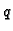 harmonijske.
Pri tom je
Iz ovih formula slijedi
Tako je funkcija
harmonijska, jer je
Označimo s
harmonijske.
Pri tom je
Iz ovih formula slijedi
Tako je funkcija
harmonijska, jer je
Označimo s 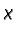 analitičku funkciju, čiji je realni dio funkcija
analitičku funkciju, čiji je realni dio funkcija 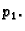 Tada je
Tada je
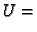
Re
![$\displaystyle \,[\bar{z}\,\varphi (z)+\chi(z)]=
\frac{1}{2}(\bar{z}\,\varphi (z)+z\,\overline{\varphi (z)}+\chi(z)+
\overline{\chi(z)}).$](img3718.gif)
Tako smo funkciju 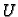 prikazali pomoću dvije analitičke funkcije
prikazali pomoću dvije analitičke funkcije 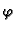 i
i
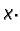
- 1.
- Koje karakteristike treba imati preslikavanje
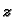 -ravnine u
-ravnine u 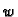 -ravninu, da bude konformno?
-ravninu, da bude konformno?
- 2.
- Kada funkcija kompleksne varijable ostvaruje konformno preslikavanje?
- 3.
- Kako glasi Riemannov teorem o konformnom preslikavanju?
- 4.
- Što je razlomljeno linearno preslikavanje, i koja su njegova svojstva?
- 5.
- Izrecite Dirichletov problem.
- 6.
- Na koji način se rješava Dirichletov problem za jedinični krug?
- 7.
- Na koji način se rješava Dirichletov problem za proizvoljno jednostruko povezano područje čiji rub sadrži više od jedne točke?
- 8.
- Kako glasi osnovna jednadžba stacionarnog, bezvrtložnog, ravninskog gibanja nestlačivog fluida?
- 9.
- Objasnite pojmove kompleksna brzina, potencijal brzine, kompleksni potencijal, funkcija toka.
- 10.
- Kako glasi Maxwellova jednadžba?
- 11.
- Što su to biharmonijske funkcije?
- 12.
- Kako se biharmonijska funkcija može opisati pomoću analitičkih funkcija?
- 1.
- Naći linearno razlomljeno preslikavanje, ako je
- (a)
-
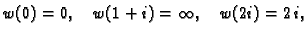
- (b)
-
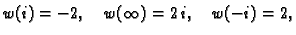
i naći u što se preslikava poluravnina 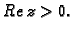
Rješenje.
- (a)
- Koeficijente linearnog razlomljenog preslikavanja ćemo dobiti
rješavajući jednadžbe
To su tri jednadžbe s četiri nepoznanice. Ako stavimo
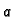 kao
parametar, dobivamo
pa je tako traženo preslikavanje
Da bismo vidjeli u što se preslika poluravnina
kao
parametar, dobivamo
pa je tako traženo preslikavanje
Da bismo vidjeli u što se preslika poluravnina
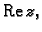 dovoljno je vidjeti u što se preslika rub poluravnine i jedna
unutrašnja točka. Imamo
pa se rub
poluravnine preslikava u kružnicu sa središtem u
dovoljno je vidjeti u što se preslika rub poluravnine i jedna
unutrašnja točka. Imamo
pa se rub
poluravnine preslikava u kružnicu sa središtem u 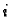 i radiusom
i radiusom
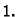 Budući da se
Budući da se 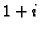 preslikava u
preslikava u 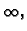 poluravnina
poluravnina
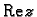 se preslikava u neograničeni dio ravnine određen ovom
kružnicom kao rubom.
se preslikava u neograničeni dio ravnine određen ovom
kružnicom kao rubom.
- (b)
- Jednadžbu iz drugog uvjeta ćemo dobiti tako da linearno
razlomljeno preslikavanje prepišemo ovako
i zatim uzmemo limes kad
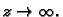 Tako imamo jednadžbe
Rješavajući ove jednadžbe uz
parametar
Tako imamo jednadžbe
Rješavajući ove jednadžbe uz
parametar 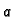 dobivamo
Tako je traženo preslikavanje
dobivamo
Tako je traženo preslikavanje
Iz zadanih točaka preslikavanja slijedi da se rub poluravnine
preslikava u kružnicu sa središtem u ishodištu i radiusom 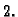 Kako
je
Kako
je 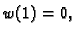 poluravnina se preslikava u ograničeni dio kompleksne
ravnine omeđen ovom kružnicom.
poluravnina se preslikava u ograničeni dio kompleksne
ravnine omeđen ovom kružnicom.





Next: Dodaci
Up: Funkcije kompleksne varijable
Previous: Integralni račun
Contents
Index
Salih Suljagic
2000-03-11
![]() područje u
područje u ![]() neka je
neka je
![]() analitička
funkcija, neka je
analitička
funkcija, neka je ![]() i neka je
i neka je
![]() Budući da je
analitička, funkcija
Budući da je
analitička, funkcija ![]() ima derivacije bilo kojeg reda. To znači da
za proizvoljan
ima derivacije bilo kojeg reda. To znači da
za proizvoljan ![]() postoji
postoji
![]() koji se nalazi na
spojnici točaka
koji se nalazi na
spojnici točaka ![]() i
i ![]() tako da vrijedi
tako da vrijedi
![]() analitička funkcija na području
analitička funkcija na području ![]() u kompleksnoj
ravnini, i
u kompleksnoj
ravnini, i
![]() za svaki
za svaki ![]() onda je funkcijom
onda je funkcijom ![]() definirano konformno preslikavanje područja
definirano konformno preslikavanje područja ![]() u
u ![]() -ravnini u
njegovu
-ravnini u
njegovu ![]() -sliku, područje
-sliku, područje ![]() u
u ![]() -ravnini. Vrijedi i obrat. Ako je
preslikavanje područja
-ravnini. Vrijedi i obrat. Ako je
preslikavanje područja ![]() u
u ![]() -ravnini u područje
-ravnini u područje ![]() u
u
![]() -ravnini konformno, onda postoji analitička funkcija
-ravnini konformno, onda postoji analitička funkcija ![]() na
na ![]() takva da je
takva da je
![]() i da preslikava
i da preslikava ![]() na
na ![]()
![]() i
i
![]() nađe funkcija koja ostvaruje konformno preslikavanje
područja
nađe funkcija koja ostvaruje konformno preslikavanje
područja ![]() na područje
na područje ![]()
![]() formulom
formulom
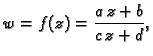 gdje je
gdje je
![]() Derivacija je
Derivacija je
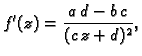
![]() koji je različit od nule, vidimo da je razlomljeno linearno
preslikavanje zadano s tri uvjeta. Tako zahtjev da određene tri
točke
koji je različit od nule, vidimo da je razlomljeno linearno
preslikavanje zadano s tri uvjeta. Tako zahtjev da određene tri
točke ![]() -ravnine budu preslikane u određene tri točke
-ravnine budu preslikane u određene tri točke ![]() -ravnine
potpuno određuje razlomljeno linearno preslikavanje. Razlomljeno
linearno preslikavanje je injekcija, tj. ne lijepi točke, i preslikava
pravce i kružnice u pravce i kružnice.
-ravnine
potpuno određuje razlomljeno linearno preslikavanje. Razlomljeno
linearno preslikavanje je injekcija, tj. ne lijepi točke, i preslikava
pravce i kružnice u pravce i kružnice.
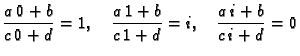
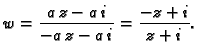
![]() imamo
imamo
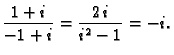
![]() i neka je dana neprekidna funkcija
i neka je dana neprekidna funkcija ![]() na
rubu
na
rubu
![]() područja
područja ![]() Treba naći funkciju
Treba naći funkciju ![]() harmonijsku
na području
harmonijsku
na području ![]() neprekidnu na rubu
neprekidnu na rubu
![]() takvu da je
takvu da je
![]() tj. treba riješiti problem
tj. treba riješiti problem
![]() neprekidna funkcija na
jediničnoj kružnici, onda je funkcija
neprekidna funkcija na
jediničnoj kružnici, onda je funkcija
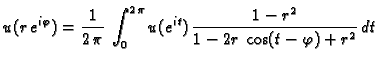
![]() proizvoljno jednostruko povezano područje čiji rub
sadrži više od jedne točke, i neka je na njegovom rubu
proizvoljno jednostruko povezano područje čiji rub
sadrži više od jedne točke, i neka je na njegovom rubu
![]() zadana neprekidna funkcija
zadana neprekidna funkcija ![]() Prema Riemannovom
teoremu postoji konformno preslikavanje
Prema Riemannovom
teoremu postoji konformno preslikavanje ![]() sa
sa ![]() na jedinični krug.
Funkcija
na jedinični krug.
Funkcija ![]() preslikava
preslikava ![]() u funkciju
u funkciju
![]() neprekidnu na
jediničnoj kružnici. Ako sada primijenimo Poissonov integral na
funkciju
neprekidnu na
jediničnoj kružnici. Ako sada primijenimo Poissonov integral na
funkciju
![]() dobit ćemo harmonijsku funkciju
dobit ćemo harmonijsku funkciju ![]() u
jediničnom krugu, koja se na jediničnoj kružnici poklapa s
u
jediničnom krugu, koja se na jediničnoj kružnici poklapa s
![]() Kompozicija
Kompozicija
![]() Jednadžba kontinuiteta
Jednadžba kontinuiteta
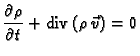
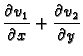
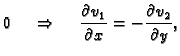
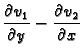
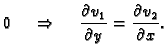
![]() na
na ![]() znači da je vektorsko
polje brzina potencijalno, tj. da postoji skalarno polje (potencijal
brzine)
znači da je vektorsko
polje brzina potencijalno, tj. da postoji skalarno polje (potencijal
brzine) ![]() na
na ![]() takvo da je
takvo da je
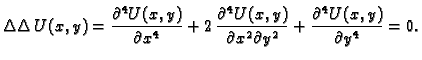
![]() proizvoljna biharmonijska funkcija. Tada je
proizvoljna biharmonijska funkcija. Tada je ![]() harmonijska, pa postoji analitička funkcija
harmonijska, pa postoji analitička funkcija ![]() takva da je
takva da je
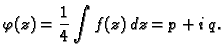
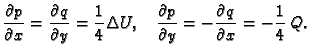
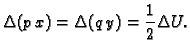
![$\displaystyle \,[\bar{z}\,\varphi (z)+\chi(z)]=
\frac{1}{2}(\bar{z}\,\varphi (z)+z\,\overline{\varphi (z)}+\chi(z)+
\overline{\chi(z)}).$](img3718.gif)
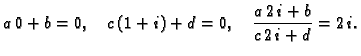
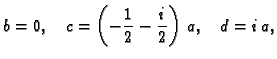
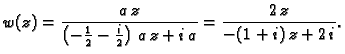
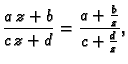
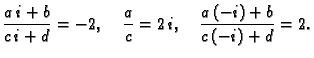
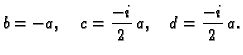
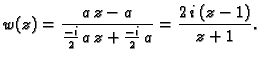
![]() Kako
je
Kako
je ![]() poluravnina se preslikava u ograničeni dio kompleksne
ravnine omeđen ovom kružnicom.
poluravnina se preslikava u ograničeni dio kompleksne
ravnine omeđen ovom kružnicom.