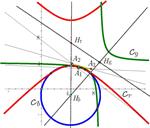
Incenter Circles, Chromogeometry, and the
Omega Triangle

Chromogeometry brings together planar Euclidean geometry, here called blue geometry, and two relativistic geometries, called red and green. We show that if a triangle has four blue Incenters and four red Incenters, then these eight points lie on a green circle, whose center is the green Orthocenter of the triangle, and similarly for the other colours. Tangents to the incenter circles yield interesting additional standard quadrangles and concurrencies. The proofs use the framework of rational trigonometry together with standard coordinates for triangle geometry, while a dilation argument allows us to extend the results also to Nagel and Speiker points.

Key words: triangle geometry, incenter circles, rational
trigonometry, chromogeometry, four-fold symmetry, Nagel
points, Spieker points, Omega triangle

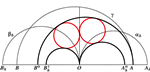
The Arbelos with Overhang

We consider a generalized arbelos consisting of three semicircles with collinear centers, in which only two of the three
semicircles touch. Many Archimedean circles of the ordinary arbelos are generalized to our generalized arbelos.

Key words: arbelos, arbelos with overhang, Archimedean
circles
Article in PDF.

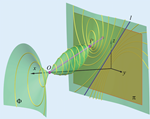
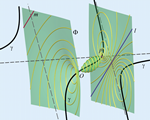
Distances and Central Projections

Given a point P in Euclidean space R³ we look for all points Q such that the length PQ of the line segments PQ from P to Q equals the length of the central image of the segment. It turns out that for any fixed point P the set of all points Q is a quartic surface \Phi. The quartic \Phi carries a one-parameter family of circles, has two conical nodes, and intersects the image plane p along a proper line and the three-fold ideal line p₂ of \pi if we perform the projective closure of the Euclidean three-space. In the following we shall describe and analyze the surface \Phi.

Key words: central projection, distance, principal line,
distortion, circular section, quartic surface, conical node

Article in PDF.

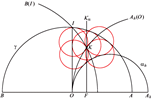
Non-standard Visualizations of Fibonacci Numbers and the Golden Mean

Fibonacci numbers and the Golden Mean are numbers and thus 0-dimensional objects. Usually, they are visualized in the Euclidean plane using squares and rectangles in a spiral arrangement. The Golden Mean, as a ratio, is an affine geometric concept and therefore Euclidean visualizations are not mandatory. There are attempts to visualize the Fibonacci number sequence and Golden Spirals in higher dimensions [11], in Minkowski planes [12], [4] and in hyperbolic planes (again [4]). The latter has to replace the not existing squares by sequences of touching circles. This article aims at visualizations in all Cayley-Klein planes and makes use of three different visualization ideas: nested sets of squares, sets of touching circles and sets of triangles that are related to Euclidean right angled triangles.

Key words: Cayley-Klein geometries, Fibonacci numbers,
Golden Mean

Article in PDF.

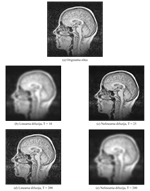
Application of Linear and Nonlinear Heat Equ-
ation in Digital Image Processing

We will explore the application of partial differential equations on digital images. We will show how to use the heat equation to eliminate noise in an image, highlight important elements and prepare it for possible further processing. We also show known heat equation's theoretical results in a methodical sequence and then derive simple numerical schemes based on the finite differences method. Guided by the idea of image structure preservation, for example edge preservation, the central part of this article introduces Perona-Malik equation as an example of a nonlinear heat equation. We conclude by comparing linear
and nonlinear heat equation application on a couple of test
images.

Key words: heat equation, Perona-Malik equation

Article in PDF.

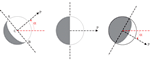
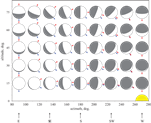
The Moon Tilt Illusion

The moon tilt illusion is the startling discrepancy between the direction of the light beam illuminating the moon and the direction of the sun. The illusion arises because the observer erroneously expects a light ray between sun and moon to appear as a line of constant slope according to the positions of the sun and the moon in the sky. This expectation does not correspond to the reality that observation by direct vision or a camera is according to perspective projection, for which the observed slope of a straight line in three-dimensional space changes according to the direction of observation. Comparing the observed and expected directions of incoming light at the moon, we derive a quantitative expression for the magnitude of the moon tilt illusion that can be applied to all configurations of sun and moon in the sky.

Key words: moon tilt, perspective projection, illusion

Article in PDF.