




Next: Homogenizacija rubnih uvjeta.
Up: Rubni problemi
Previous: Početni uvjeti
Sadržaj
Indeks
Linearnost
Opća jednadžba u primjerima koje smo promatrali, nakon uvrštenja
drugog zakona ponašanja je
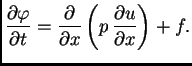 |
(2.6) |
Funkciju 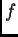 zovemo slobodnim članom. Ako je
zovemo slobodnim članom. Ako je 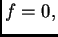 onda jednadžbu
onda jednadžbu
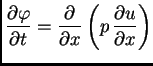 |
(2.7) |
zovemo homogenom, u protivnom je zovemo
nehomogenom.
Ograničimo razmatranje na one primjere u kojima je prvi zakon
ponašanja glasio
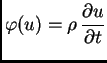 ili ili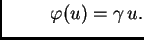 |
(2.8) |
Interesira nas kakvu strukturu ima skup svih rješenja rubnog problema
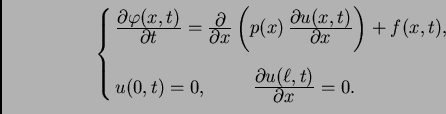 |
(2.9) |
U tu svrhu promatrajmo najprije rubni problem s homogenom jednadžbom,
tj. slučaj kad je
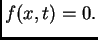
Teorem 14
Neka su
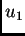
i
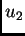
dva rješenja rubnog problema
(
2.9) s pripadnom homogenom jednadžbom, i
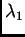
i
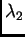
proizvoljni brojevi. Tada je
također rješenje istog rubnog
problema (
2.9).
Dokaz. U svrhu dokaza napišimo
jednadžbu drukčije
Bez
obzira koji 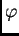 iz (2.8) bio u jednadžbi, vrijedi
Također
Prema
tome
Dakle,
iz (2.8) bio u jednadžbi, vrijedi
Također
Prema
tome
Dakle,
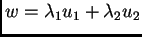 rješava
jednadžbu. Ta funkcija zadovoljava i rubne uvjete, jer je
rješava
jednadžbu. Ta funkcija zadovoljava i rubne uvjete, jer je
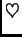
Iz ovog teorema slijedi da je skup svih rješenja homogene jednadžbe
vektorski prostor (skup svih linearnih kombinacija linearno nezavisnih
rješenja).
Za rješenja rubnog problema (2.9) s nehomogenom
jednadžbom imamo sljedeće tvrdnje.
Teorem 15
Neka je
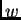
rješenje rubnog problema (
2.9) s
nehomogenom jednadžbom, te

rješenje rubnog problema
(
2.9) s homogenom jednadžbom. Tada je
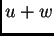
rješenje
rubnog problema (
2.9) s nehomogenom jednadžbom.
Dokaz. Koristeći svojstva funkcije
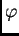 iz dokaza prethodnog teorema, možemo napisati
iz dokaza prethodnog teorema, možemo napisati
Dakle 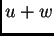 rješava
nehomogenu jednadžbu. Osim toga
rješava
nehomogenu jednadžbu. Osim toga 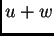 očito zadovoljava i rubne
uvjete.
očito zadovoljava i rubne
uvjete.
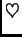
Teorem 16
Neka su
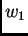
i
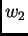
dva rješenja rubnog problema
(
2.9) s nehomogenom jednadžbom. Tada je
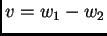
rješenje rubnog problema (
2.9) s homogenom
jednadžbom.
Dokaz.
Osim toga 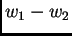 očito
zadovoljava i rubne uvjete.
očito
zadovoljava i rubne uvjete.
Na temelju ovih teorema imamo sljedeći zaključak.
Neka je 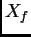 skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je
skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je 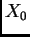 skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
gdje je 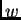 jedno (partikularno)
rješenje rubnog problema (2.9) s nehomogenom jednadžbom.
jedno (partikularno)
rješenje rubnog problema (2.9) s nehomogenom jednadžbom.
Subsections





Next: Homogenizacija rubnih uvjeta.
Up: Rubni problemi
Previous: Početni uvjeti
Sadržaj
Indeks
2001-10-26
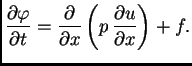
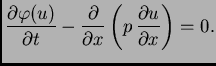
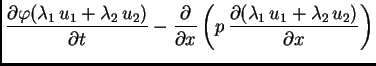
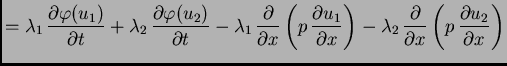
![$\displaystyle =
\lambda_1\,\left[\frac{\partial\varphi (u_1)}{\partial t} -
\fr...
...partial}{\partial
x}\left(p\,\frac{\partial u_2}{\partial x}\right)\right] = 0.$](img1265.png)
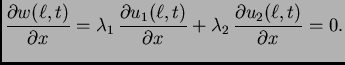
![]() iz dokaza prethodnog teorema, možemo napisati
iz dokaza prethodnog teorema, možemo napisati
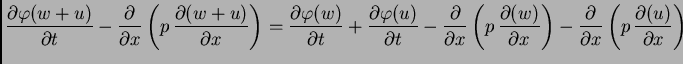

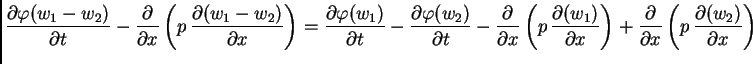
![$\displaystyle = \frac{\partial\varphi(w_1)}{\partial t} -
\frac{\partial}{\part...
...partial x}\left(p\,\frac{\partial (w_2)}{\partial
x}\right)\right] = f - f = 0.$](img1277.png)
![]() skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je
skup svih rješenja rubnog problema (2.9) s
nehomogenom jednadžbom. Neka je ![]() skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je
skup svih rješenja rubnog
problema (2.9) s homogenom jednadžbom. Tada je