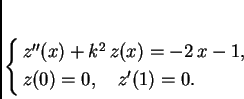Homogenizacija rubnih uvjeta.

Ako su rubni uvjeti nehomogeni, onda linearne kombinacije više ne zadovoljavaju iste rubne uvjete, pa gornji teoremi više ne vrijede. Prema tome pogodno je imati homogene rubne uvjete. To se može postići na sljedeći način. Neka je dan na pr. sljedeći rubni problem

$$\begin{array}{l} \rho\,\frac{\texts... ...ial x}}\right)+f(x,t),\\ [3mm] u(0,t)=a,\hspace{1cm}u(\ell,t)=b. \end{array}$$

Izaberimo proizvoljnu što jednostavniju funkciju $v(x)$ klase $C^2$ ali tako da zadovoljava rubne uvjete

$$v(0) = a,\hspace{1cm}v(\ell) = b.$$

Stavimo $\tilde{u}(x,t)=u(x,t)-v(x).$ Tada funkcija $\tilde{u}$ zadovoljava homogene rubne uvjete

$$\tilde{u}(0,t) = u(0,t) - v(0) = 0,\hspace{1cm}\tilde{u}(0,t) = u(\ell,t) - v(\ell) = 0.$$

S druge strane, da bismo vidjeli koju jednadžbu zadovoljava $\tilde{u},$ uvrstimo $u(x,t) = \tilde{u}(x,t) + v(x)$ u jednadžbu iz rubnog problema

$$\rho\,\frac{\partial^2 (\tilde{u}(x,t)+v(x))}{\partial t^2} = \fr... ...ial x}\left(p\,\frac{\partial (\tilde{u}(x,t)+v(x))}{\partial x}\right)+f(x,t),$$

$$\rho\,\frac{\partial^2 \tilde{u}(x,t)}{\partial t^2} = \frac{\par... ...\partial}{\partial x}\left(p\,\frac{\partial v(x)}{\partial x}\right) + f(x,t),$$

$$\rho\,\frac{\partial^2 \tilde{u}(x,t)}{\partial t^2} = \frac{\par... ... x}\left(p\,\frac{\partial \tilde{u}(x,t)}{\partial x}\right) + \tilde{f}(x,t),$$

gdje je

$$\tilde{f}(x,t) = \frac{\partial}{\partial x}\left(p\,\frac{\partial v(x)}{\partial x}\right) + f(x,t).$$

Primjer 2.5   Homogenizirati rubni problem

$$% latex2html id marker 34244 \begin{cases} y''(x) + k^2\,y(x) = 0,& \\ y(0) = 1,\quad y'(1) = 2. \end{cases}$$

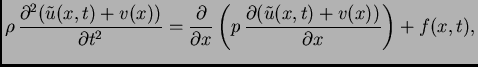
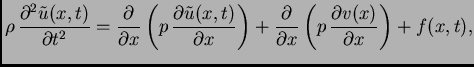
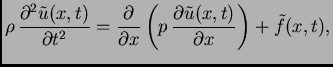
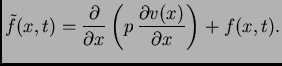
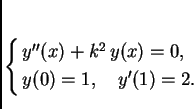
Rješenje. Izaberimo najjednostavniju funkciju $v(x)$ takvu da funkcija

$$z(x) = y(x) + v(x)$$

zadovoljava homogene rubne uvjete, tj.

$$z(0) = 0,\quad z'(1) = 0.$$

Zbog toga što se radi o uvjetu u samo dvije točke, dovoljno je uzeti

$$v(x) = A\,x + B.$$

Tako je

$$z(0) = y(0) + v(0) = 1 + v(0) = 0,$$

$$z'(1) = y'(1) + v'(1) = 2 + v'(1) = 0.$$

Odatle $v(0)=-1,$ $v'(1)=-2.$ Slijedi $A=-2,$ $B=-1.$ Tako je

$$z(x) = y(x) -2\,x - 1,$$

pa kad $y$ izračunamo odavde i uvrstimo u jednadžbu, imamo rubni problem

$$% latex2html id marker 34270 \begin{cases} z''(x) + k^2\,z(x) = - 2\,x - 1,& \\ z(0) = 0,\quad z'(1) = 0. \end{cases}$$