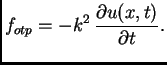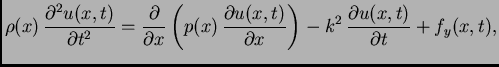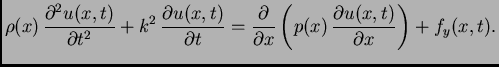Next: Ravnoteža žice.
Up: Poprečne oscilacije žice
Previous: Zakon održanja količine gibanja
Sadržaj
Indeks
Zakoni ponašanja
Označimo s 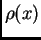 linearnu gustoću mase žice u točki
linearnu gustoću mase žice u točki 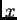 u čas
u čas
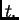 Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki
Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki 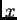 u čas
u čas 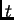 jednaka
umnošku mase po jedinici duljine u točki
jednaka
umnošku mase po jedinici duljine u točki 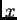 i brzine u točki
i brzine u točki 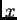 u
čas
u
čas 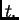 Tako imamo prvi zakon ponašanja
Tako imamo prvi zakon ponašanja
Usvojimo sada sljedeća pojednostavljenja.
Pretpostavljamo da se gibanje odvija u ravnini 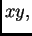 i to tako da je
i to tako da je
tj. tako da je komponenta
progiba u smjeru osi 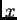 jednaka nuli. U skladu s ovom pretpostavkom
možemo progib smatrati skalarnim poljem
jednaka nuli. U skladu s ovom pretpostavkom
možemo progib smatrati skalarnim poljem 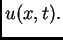
Promatrat ćemo male progibe žice, tako da možemo pretpostaviti da
je
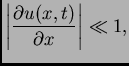
za svaki
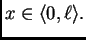
U tom
slučaju ćemo reći da je deformacija mala. Odatle
odnosno
To znači da je apsolutni
prirast progiba u odnosu na progib u ishodištu vrlo malen prema
duljini žice.
Slika 2.3:
Kontaktna sila pri malim deformacijama
|
|
Budući da je deformacija mala, možemo pretpostaviti da je kontaktna
sila
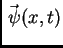 u točki
u točki 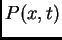 kolinearna s jediničnim
tangencijalnim vektorom na progib žice
kolinearna s jediničnim
tangencijalnim vektorom na progib žice 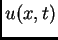 u točki
u točki 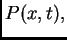 tj.
tj.
Funkcija 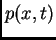 se
zove napetost
žice u točki
se
zove napetost
žice u točki 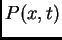 u čas
u čas 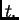 U daljnjem ćemo pretpostavljati
da napetost ne ovisi o vremenu, i da je u svakoj točki pozitivna,
tj. da je
U daljnjem ćemo pretpostavljati
da napetost ne ovisi o vremenu, i da je u svakoj točki pozitivna,
tj. da je
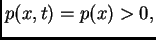
za svaki
![$\displaystyle x \in [0,\ell].$](img1108.png)
Tako je
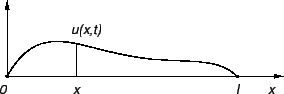
Progib
možemo shvatiti kao krivulju u ravnini s parametrizacijom
![$ ([0,\ell],\vec{\,r}),$](img1110.png) gdje je
gdje je
Slika 2.4:
Progib kao krivulja u ravnini.
|
|
Tada je
Budući da je
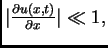 možemo zanemariti
možemo zanemariti
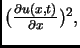 pa imamo
odnosno imamo drugi zakon
ponašanja
pa imamo
odnosno imamo drugi zakon
ponašanja
Vanjska sila po jedinici duljine djeluje u ravnini 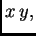 pa možemo
pisati
pa možemo
pisati
Slika 2.5:
Vanjska sila po jedinici duljine
|
|
Ako se s ovim vratimo u diferencijalnu jednadžbu
(2.1), imamo
što se
raspada na dvije skalarne jednadžbe
Prva jednadžba omogućava izračunavanje napetosti žice. Da bi
napetost bila neovisna o vremenu, nužno mora 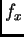 biti neovisno o
vremenu. Tako imamo
biti neovisno o
vremenu. Tako imamo
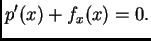 |
(2.2) |
Integrirajmo ovu jednadžbu
Ako vanjska sila
djeluje poprečno na žicu, onda je
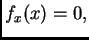 pa je
pa je
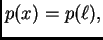 tj. napetost je konstantna, i jednaka napetosti na desnom
rubu. Ako vanjska sila ima komponentu u smjeru osi
tj. napetost je konstantna, i jednaka napetosti na desnom
rubu. Ako vanjska sila ima komponentu u smjeru osi 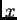 različitu od
nule, onda napetosti na desnom rubu treba dodati još doprinos od
vanjske sile po jedinici duljine.
različitu od
nule, onda napetosti na desnom rubu treba dodati još doprinos od
vanjske sile po jedinici duljine.
Druga jednadžba
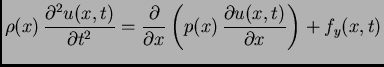 |
(2.3) |
se zove
valna jednadžba. To je parcijalna diferencijalna
jednadžba. Napetost izračunamo iz prve jednadžbe, 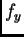 je
zadano time što je zadana vanjska sila po jedinici duljine.
je
zadano time što je zadana vanjska sila po jedinici duljine. 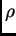 je zadana linijska gustoća mase žice. Nepoznanica u jednadžbi je
progib
je zadana linijska gustoća mase žice. Nepoznanica u jednadžbi je
progib 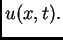 Osnovni problem je, dakle, izračunati
Osnovni problem je, dakle, izračunati 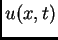 iz
valne jednadžbe. Ako pretpostavimo da je napetost konstantna duž
žice, valna jednadžba poprima oblik
Također
je prirodno pretpostaviti da je
iz
valne jednadžbe. Ako pretpostavimo da je napetost konstantna duž
žice, valna jednadžba poprima oblik
Također
je prirodno pretpostaviti da je
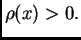 Tada možemo podijeliti
jednadžbu s
Tada možemo podijeliti
jednadžbu s 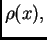 pa imamo
gdje je
pa imamo
gdje je 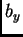 sila po jedinici duljine i po jedinici gustoće mase u
smjeru osi
sila po jedinici duljine i po jedinici gustoće mase u
smjeru osi 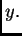 (U ovom slučaju to je akceleracija vanjske sile u
smjeru osi
(U ovom slučaju to je akceleracija vanjske sile u
smjeru osi 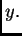 )
)
Ako žica oscilira u nekom sredstvu koje pruža otpor gibanju, onda
treba uzeti u obzir silu otpora. Budući da su oscilacije male,
može se pretpostaviti da sredstvo reagira kao elastično, tj. da
je sila otpora po jedinici duljine proporcionalna progibu i
suprotnog smjera
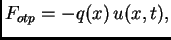 gdje je
gdje je
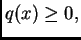 za
za
![$ x \in
[0,\ell]\,$](img1044.png) faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
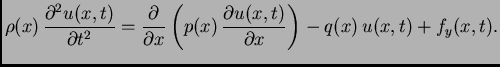
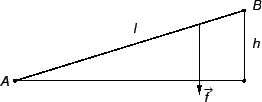
Primjer 2.1
Homogena teška žica, gustoće mase
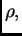
duljine
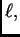
razapeta
je između točaka
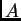
na zemlji i
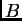
na visini
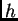
kao na slici.
Naći napetost žice u svakoj točki, ako je žica napeta u točki
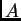
napetošću
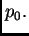
Rješenje. Kad kažemo teška žica, mislimo na to da se njezina težina ne
može zanemariti. To znači da na žicu djeluje vanjska sila, sila
teža. U izvodu jednadžbi mi smo koristili linearnu gustoću vanjske
sile (silu po jedinici duljine). Ona je ovdje u svakoj točki po
iznosu 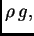 a po smjeru okomita je prema površini zemlje.
a po smjeru okomita je prema površini zemlje.
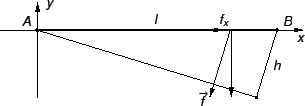
Postavimo koordinatni sustav tako da os 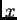 prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
Iz slike vidimo (pomoću sličnosti trokuta) da je
Integrirajmo jednadžbu (
2.2) od 0 do
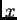
Ako žica nije homogena,
onda treba znati gustoću mase kao funkciju od
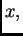
tj. tada
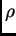
nije konstanta, već funkcija od
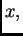
pa je tada
Primjer 2.2
Izvesti jednadžbu malih oscilacija napete žice u sredstvu s
otporom, koji je proporcionalan brzini.
Rješenje. Budući da se radi o malim oscilacijama, možemo usvojiti ona
pojednostavnjenja i zanemarivanja, koja smo usvojili kod izvoda
valne jednadžbe (2.3). Dakle, možemo pretpostaviti da
žica oscilira u smjeru okomitom na njezin ravnotežni
položaj. U tom smjeru se javlja i sila otpora, no kako se ona opire
kretanju, ona djeluje suprotno od smjera kretanja. Postavimo
koordinatni sustav tako da žica u ravnoteži leži na osi 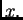 Tada
se kretanje događa u smjeru osi
Tada
se kretanje događa u smjeru osi 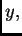 pa imamo jednadžbu za
napetost
pa imamo jednadžbu za
napetost
U smjeru osi
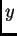
osim vanjske sile po jedinici
duljine i kontaktne sile imamo još i silu otpora po jedinici duljine
Prema tome sada valna jednadžba glasi
odnosno
Subsections





Next: Ravnoteža žice.
Up: Poprečne oscilacije žice
Previous: Zakon održanja količine gibanja
Sadržaj
Indeks
2001-10-26
![]() linearnu gustoću mase žice u točki
linearnu gustoću mase žice u točki ![]() u čas
u čas
![]() Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki
Linearna gustoća mase je masa po jedinici duljine. Tada je
količina gibanja po jedinici duljine u točki ![]() u čas
u čas ![]() jednaka
umnošku mase po jedinici duljine u točki
jednaka
umnošku mase po jedinici duljine u točki ![]() i brzine u točki
i brzine u točki ![]() u
čas
u
čas ![]() Tako imamo prvi zakon ponašanja
Tako imamo prvi zakon ponašanja
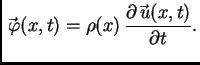
![]() i to tako da je
i to tako da je
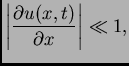 za svaki
za svaki 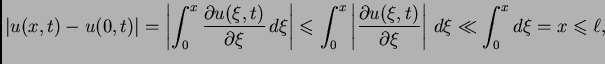
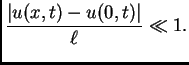
![]() u točki
u točki ![]() kolinearna s jediničnim
tangencijalnim vektorom na progib žice
kolinearna s jediničnim
tangencijalnim vektorom na progib žice ![]() u točki
u točki ![]() tj.
tj.
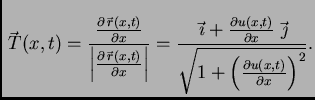
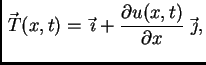
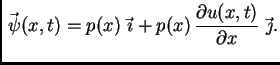
![]() pa možemo
pisati
pa možemo
pisati
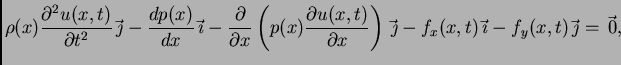
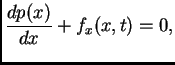
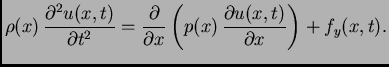
![]() biti neovisno o
vremenu. Tako imamo
biti neovisno o
vremenu. Tako imamo
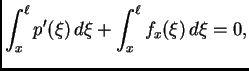
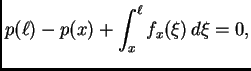
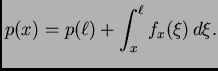
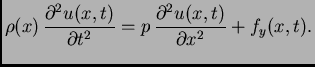
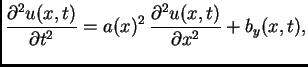
![]() gdje je
gdje je
![]() za
za
![]() faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
faktor proporcionalnosti. U tom slučaju imamo
jednadžbu oscilacija
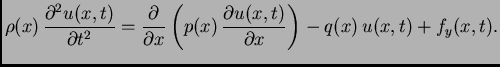
![]() a po smjeru okomita je prema površini zemlje.
a po smjeru okomita je prema površini zemlje.
![]() prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
prolazi žicom. Gustoća
sile se može rastaviti na komponentu koja djeluje duž žice i onu
drugu koja je okomita na žicu. Napetosti pridonosi samo komponenta
duž žice.
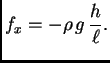
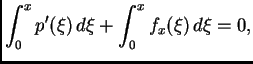
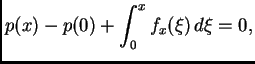
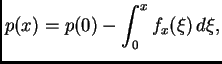
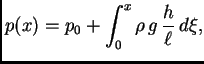
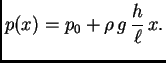
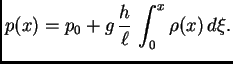
![]() Tada
se kretanje događa u smjeru osi
Tada
se kretanje događa u smjeru osi ![]() pa imamo jednadžbu za
napetost
pa imamo jednadžbu za
napetost