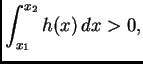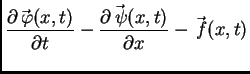Next: Zakoni ponašanja
Up: Poprečne oscilacije žice
Previous: Poprečne oscilacije žice
Sadržaj
Indeks
Zakon održanja količine gibanja
Uočimo proizvoljan komad žice
![$ D=[x_1,x_2].$](img1054.png)
Ukupna količina gibanja
tog dijela žice u čas 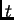 je
a ukupna količina gibanja komada žice
je
a ukupna količina gibanja komada žice 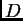 po jedinici vremena
je derivacija ukupne količine gibanja po vremenu
po jedinici vremena
je derivacija ukupne količine gibanja po vremenu
Količina gibanja po jedinici vremena komada žice 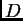 u čas
u čas 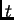 uslijed djelovanja vanjske sile je
uslijed djelovanja vanjske sile je
Količina gibanja koja se po jedinici vremena prenese na 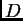 u čas
u čas
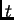 na desnom rubu, u točki
na desnom rubu, u točki 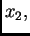 je
je
a količina gibanja koja se po jedinici
vremena prenese na 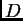 u čas
u čas 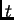 na lijevom rubu, u točki
na lijevom rubu, u točki 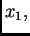 je
jer smo za pozitivan smjer prenošenja
količine gibanja duž žice izabrali smjer s desna na lijevo.
je
jer smo za pozitivan smjer prenošenja
količine gibanja duž žice izabrali smjer s desna na lijevo.
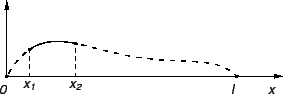
Slika 2.2:
Kontaktna sila na rubovima
|
|
Ukupna količina gibanja po jedinici vremena komada 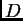 jednaka je
zbroju količina gibanja po jedinici vremena uslijed djelovanja
preostalog dijela žice i uslijed djelovanja vanjske sile. Dakle
jednaka je
zbroju količina gibanja po jedinici vremena uslijed djelovanja
preostalog dijela žice i uslijed djelovanja vanjske sile. Dakle
Ova jednadžba se zove
jednadžba balansa ili zakon
održanja količine gibanja. (Uočite
da se ovdje radi o poznatom fizikalnom zakonu da je promjena količine
gibanja nekog tijela u jedinici vremena jednaka zbroju sila koje
djeluju na tijelo.)
Pretostavka da je ukupna količina gibanja po jedinici vremena
neprekidna
funkcija, što fizikalno znači da se brzina promjene količine
gibanja neprekidno mijenja (neprekidnost sile), omogućava da
primijenimo Leibnizovo
pravilo za deriviranje pod znakom integrala. Zatim, ako još
shvatimo kao jednu stranu Newton-Leibnizove formule (osnovne formule
integralnog računa), onda imamo
odnosno
Naglasimo da ovaj izvod
vrijedi za proizvoljan segment žice
![$ [x_1,x_2].$](img1069.png)
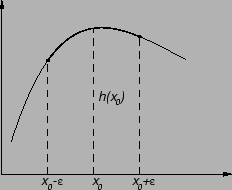
Lema 1
(Osnovna lema) Neka je skalarna funkcija
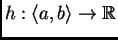
neprekidna na
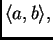
i neka je
za svaki par brojeva
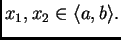
Tada je 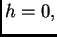 tj.
tj. 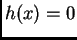 za svaki
za svaki
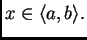
Dokaz. Pretpostavimo suprotno, da
postoji 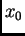 takav da je
takav da je 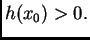 (Slično ide dokaz uz
pretpostavku
(Slično ide dokaz uz
pretpostavku 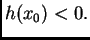 ) Zbog neprekidnosti funkcije
) Zbog neprekidnosti funkcije 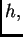 postoji
postoji
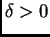 takav da
takav da
To
znači da je 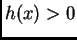 za
za
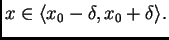 Ako izaberemo
Ako izaberemo
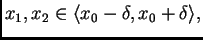 onda
je
što je u kontradikciji s
pretpostavkom u teoremu.
onda
je
što je u kontradikciji s
pretpostavkom u teoremu.
Podintegralna funkcija
je
vektorska. Iščezavanje njezinog integrala na proizvoljnom segmentu
![$ [x_1,x_2]$](img1089.png) povlači iščezavanje integrala svake skalarne komponente
na tom segmentu. To, prema osnovnoj lemi povlači da je svaka skalarna
komponenta nulfunkcija. Slijedi
povlači iščezavanje integrala svake skalarne komponente
na tom segmentu. To, prema osnovnoj lemi povlači da je svaka skalarna
komponenta nulfunkcija. Slijedi
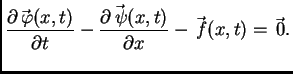 |
(2.1) |
Ova jednadžba predstavlja zakon
održanja količine gibanja u diferencijalnom obliku.
Ovo je opća jednadžba koja vrijedi za bilo kako napetu žicu od bilo
kakvog materijala. Karakteristike materijala i način na koji je žica
napeta opisuju se vezama između gore navedenih vektorskih polja. Te
veze se zovu zakoni ponašanja.





Next: Zakoni ponašanja
Up: Poprečne oscilacije žice
Previous: Poprečne oscilacije žice
Sadržaj
Indeks
2001-10-26
![]()
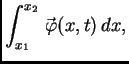
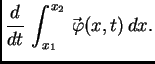
![]() u čas
u čas ![]() uslijed djelovanja vanjske sile je
uslijed djelovanja vanjske sile je
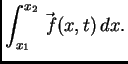
![]() u čas
u čas
![]() na desnom rubu, u točki
na desnom rubu, u točki ![]() je
je
![]() jednaka je
zbroju količina gibanja po jedinici vremena uslijed djelovanja
preostalog dijela žice i uslijed djelovanja vanjske sile. Dakle
jednaka je
zbroju količina gibanja po jedinici vremena uslijed djelovanja
preostalog dijela žice i uslijed djelovanja vanjske sile. Dakle
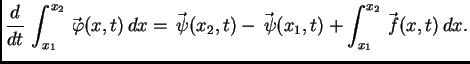
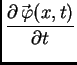
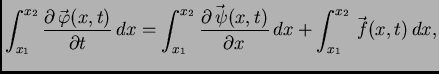
![$\displaystyle \int_{x_1}^{x_2} \left[\frac{\partial\vec{\,\varphi}(x,t)}{\parti...
...\partial\vec{\,\psi}(x,t)}{\partial x} -
\vec{\,f}(x,t)\right]\,dx = \vec{\,0}.$](img1068.png)
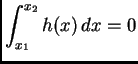
![]() tj.
tj. ![]() za svaki
za svaki
![]()
![]() takav da je
takav da je ![]() (Slično ide dokaz uz
pretpostavku
(Slično ide dokaz uz
pretpostavku ![]() ) Zbog neprekidnosti funkcije
) Zbog neprekidnosti funkcije ![]() postoji
postoji
![]() takav da
takav da