Druga metoda, Eulerova, se sastoji u tome da se rješenje pripadnog homogenog sustava pretpostavi u obliku
![% latex2html id marker 33042
$\displaystyle \boldsymbol{C}= \left[ \begin{array}{c} C_1 \\ C_2 \\ \vdots \\ C_n
\end{array} \right].$](img921.png)
Rješenje. Najprije promatramo pripadni homogeni sustav
![\begin{displaymath}
% latex2html id marker 33055
\left[
\begin{array}{c}
y(x)...
...ft[ \begin{array}{c}
y(x) \\
z(x)
\end{array}
\right].\end{displaymath}](img926.png)
![% latex2html id marker 33057
$\displaystyle \left[
\begin{array}{c}
y(x) \\
...
...t] = e^{\lambda x} \left[ \begin{array}{c}
C_1 \\
C_2
\end{array}
\right].$](img927.png)
| 0 | |||
![% latex2html id marker 33083
$\displaystyle \left[ \begin{array}{r} 1 \\ -1 \end{array}\right].$](img936.png)
![% latex2html id marker 33091
$\displaystyle \left[ \begin{array}{r} 1 \\ \frac{1}{4} \end{array} \right]. $](img939.png)
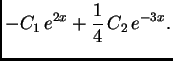 |
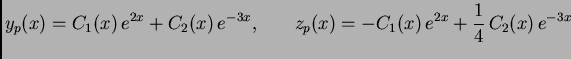
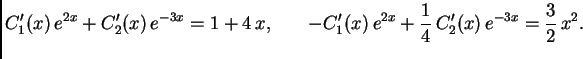
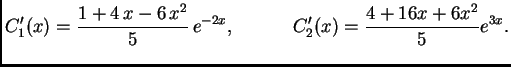
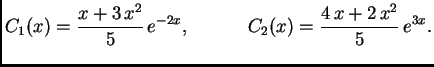

Ako sustav rješavamo Eulerovom metodom, onda se može dogoditi da neka
vlastita vrijednost od ![]() ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
ima kratnost veću od 1. Tada razlikujemo dva
slučaja.
a) Vlastitoj vrijednosti je pridruženo onoliko linearno nezavisnih vlastitih vektora kolika ja njena kratnost.
b) Vlastitoj vrijednosti pripada manje linearno nezavisnih vlastitih vektora nego što je njena kratnost.
Pogledajmo na primjerima kako se ti problemi rješavaju.
Rješenje. Matrica sustava je
![% latex2html id marker 33121
$ \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1
\end{array} \right]$](img950.png) i prema tome očigledno je
i prema tome očigledno je
![]() kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
kratnosti 2.
Nadalje, svaki vektor je vlastiti, pa možemo naći dva linearno nezavisna
vlastita vektora. Tu se dakle radi o slučaju a), pa je rješenje
![\begin{displaymath}
% latex2html id marker 33125
\left[
\begin{array}{c} y \\ ...
...C_2\,e^x \left[
\begin{array}{c} 0 \\ 1 \end{array}
\right],\end{displaymath}](img951.png)
Rješenje. Matrica sustava je
![% latex2html id marker 33134
$ \left[ \begin{array}{cc} 1 & 1 \\ 0 & 1
\end{array} \right],$](img955.png) pa je
pa je
![]() kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
kratnosti 2. Traženje vlastitih
vektora nas vodi do sustava
![% latex2html id marker 33148
$ \; C_1 \left[ \begin{array}{c} 1 \\ 0 \end{array} \right].$](img959.png) Ti vektori čine jednodimenzionalan vektorski prostor, pa ne postoje dva
linearno nezavisna vektora. To je prema tome slučaj b). Riješimo taj
zadatak prvom metodom. Deriviranje prve jednadžbe dovodi do
Ti vektori čine jednodimenzionalan vektorski prostor, pa ne postoje dva
linearno nezavisna vektora. To je prema tome slučaj b). Riješimo taj
zadatak prvom metodom. Deriviranje prve jednadžbe dovodi do
![% latex2html id marker 33166
$\displaystyle \left[ \begin{array}{c} y \\ z \end...
...array} \right] +C_2\,e^x
\left[ \begin{array}{c} x \\ 1 \end{array} \right] .$](img967.png)
Rješenje. Ovaj sustav ima rješenja
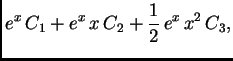 |
|||
![% latex2html id marker 33207
$\displaystyle \boldsymbol{y}= C_1\,e^x \left[
\be...
...\left[
\begin{array}{c}
\frac{1}{2}\,x^2 \\
x \\
1
\end{array}
\right].$](img980.png)
Neki put se ne mogu lagano eliminirati sve nepoznate funkcije osim jedne kao
što se to radi u prvoj metodi. Pokušajte na primjer riješiti objema
metodama slijedeći primjer
U posljednjim primjerima smo rješavali homogene sustave radi jednostavnosti. Da su bili nehomogeni, varijacijom konstanti dobili bismo partikularno rješenje.