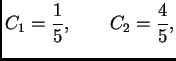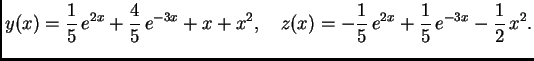Jedna od metoda se sastoji u tome da se višestrukim deriviranjem
jednadžbi izbace sve nepoznate funkcije osim jedne. Na taj način dolazimo
do jedne linearne diferencijalne jednadžbe 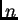 -tog reda, koju zatim
rješavamo poznatim metodama.
-tog reda, koju zatim
rješavamo poznatim metodama.
Primjer 1.29
Treba naći opće rješenje sustava
Rješenje.
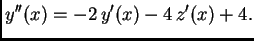 |
(1.13) |
Iz prve jednadžbe izračunamo
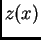
, uvrstimo u drugu i zatim
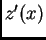
iz
druge uvrstimo u (
1.13). Dobivamo
Opće rješenje ove jednadžbe je
Uvrštavanjem u prvu jednadžbu možemo naći
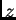
:
Dakle
pa vidimo da je
Specijalno, ako je početni uvjet
uvrštavanjem u opće rješenje dobivamo
i prema tome rješenje je
To rješenje vidimo na sljedećoj slici
Slika 1.28:
Rješenje sustava diferencijalnih jednadžbi, uz zadani početni uvjet.
|
|
![]() -tog reda, koju zatim
rješavamo poznatim metodama.
-tog reda, koju zatim
rješavamo poznatim metodama.
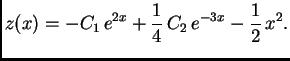
![\begin{displaymath}
% latex2html id marker 33025
\left[
\begin{array}{c}
y(x)...
...array}{c}
x+x^2 \\
-\frac{1}{2} x^2
\end{array}
\right],\end{displaymath}](img914.png)
![\begin{displaymath}
% latex2html id marker 33027
\boldsymbol{u}_1=e^{2x}\,\left[...
...\begin{array}{r}
1 \\
-\frac{1}{2}
\end{array}
\right]. \end{displaymath}](img915.png)