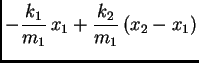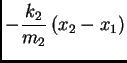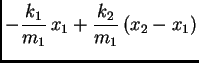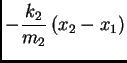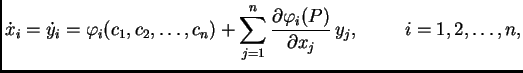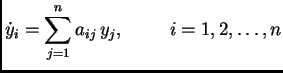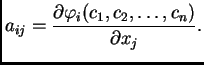Primjer 1.26
Neka su dvije mase spojene oprugama za fiksnu točku kao na slici
1.27.
Slika 1.27:
Sustav od dva harmonijska oscilatora: a) ravnotežni položaj, b) u nekom trenutku 
|
|
Ako zanemarimo otpor sredstva i težinu, onda za male oscilacije (u okviru
kojih vrijedi Hookeov zakon) imamo
Brojevi
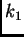
i
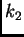
su pozitivni i oni karakteriziraju opruge.
Oscilacije ovog sistema će biti potpuno zadane ako definiramo u čas
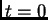
početne položaje i početne brzine:
Stavimo
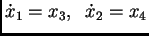
. Dobivamo sustav diferencijalnih
jednadžbi
uz početni uvjet
Osim što ovaj primjer pokazuje kako modeliranje konkretnog fizikalnog
problema dovodi do sustava diferencijalnih jednadžbi, on pokazuje također
kako se sustav u kojem se pojavljuju derivacije višeg reda može svesti na
sustav u kojem dolaze samo prve derivacije. Cijena za to je povećanje broja
jednadžbi, no to pokazuje da se možemo ograničiti na razmatranje sustava u
kojima dolaze samo prve derivacije.
Primjer 1.27
Dajmo jedan općenitiji primjer. Neka je fizikalni sustav
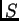
u
nekom vremenskom trenutku
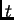
u potpunosti zadan s
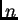
veličina,
koje opisujemo kao funkcije vremena
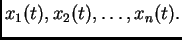
Pretpostavimo zatim da brzina promjene tih veličina ovisi
samo o njima samima. To se matematički izražava ovako
Ponašanje sustava
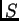
ovisi
još o stanju u kojem se nalazi u početnom trenutku. To zadajemo
početnim uvjetom za svaku veličinu
Posebno interesantne su one vrijednosti
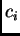
za koje je
Tada je
brzina promjene veličina
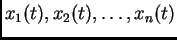
jednaka je nuli, pa se sustav
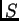
nalazi u ravnoteži. Pitanje je da li je ta ravnoteža stabilna. To
ispitujemo na taj način da sustav
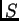
pomaknemo malo iz položaja
ravnoteže i ustanovimo što se događa. Stavimo
i uvrstimo u
diferencijalne jednadžbe
Uz
dodatni uvjet da funkcije
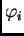
imaju neprekidne derivacije,
možemo primijeniti teorem srednje vrijednosti
gdje je
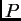
stanje sustava između
stanja
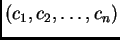
i
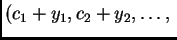
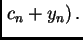
Budući da su pomaci iz
ravnotežnog stanja maleni, možemo umjesto
staviti
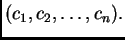
Uzimajući u obzir
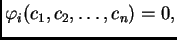
imamo
gdje je