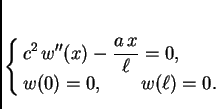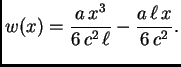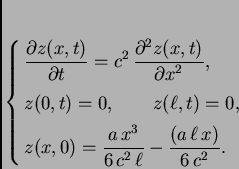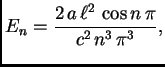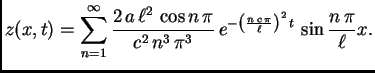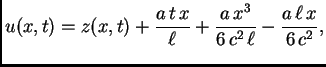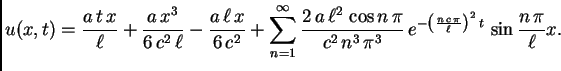Primjer 2.18
Naći raspodjelu temperature u homogenom tankom štapu, duljine
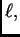
bočno toplinski izoliranom, ako se na lijevom kraju
održava temperatura
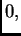
a na desnom se mijenja s vremenom po
formuli
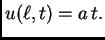
Početna temperatura štapa je
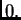
Rješenje. Rubno-početni problem glasi
Najprije treba homogenizirati rubne uvjete. Očito funkcija
zadovoljava homogene rubne
uvjete. Pripadni rubno-početni problem za
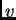
je
Sada homogeniziramo jednadžbu. Stavimo
gdje je
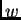
rješenje problema
Rješenje ovog problema je
Na taj način smo
homogenizirali rubne uvjete i jednadžbu, ali se
nehomogenost pojavila u početnom uvjetu. Tako
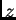
rješava sljedeći rubno-početni problem
pa je rješenje rubnog problema za
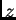
Rješenje početnog problema je
dakle
![]() i
i ![]() (v. 2.1.4) konstante, i
neka je
(v. 2.1.4) konstante, i
neka je
![]() Tada je rubno-početni problem
provođenja zadan kako slijedi
Tada je rubno-početni problem
provođenja zadan kako slijedi
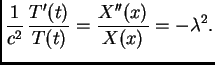
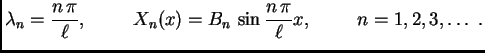
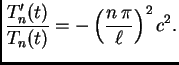
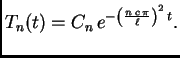
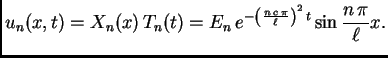
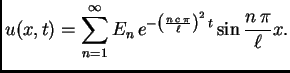
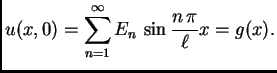
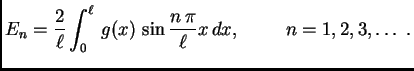
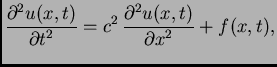
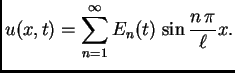
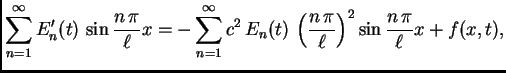
![$\displaystyle \sum_{n=1}^{\infty}
\left[E'_n(t) + \left(c\,\frac{n\,\pi}{\ell}\right)^2E_n(t)\right]
\,\sin\frac{n\,\pi}{\ell}x = f(x,t).$](img1783.png)
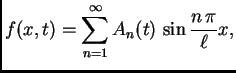
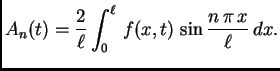
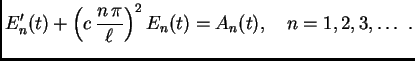
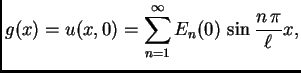
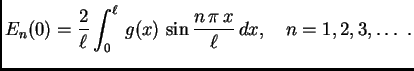
![\begin{displaymath}
% latex2html id marker 35609
\begin{cases}
\frac{\textstyl...
...0,\qquad u(\ell,t)=a\,t,& \\ [1mm]
u(x,0) = 0.
\end{cases}
\end{displaymath}](img1790.png)
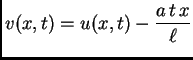
![\begin{displaymath}
% latex2html id marker 35615
\begin{cases}
\displaystyle \...
...)=0,\qquad v(\ell,t)=0,& \\ [1mm]
v(x,0) = 0.
\end{cases}
\end{displaymath}](img1793.png)