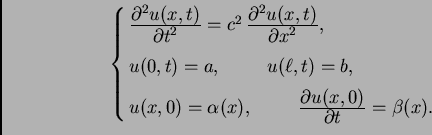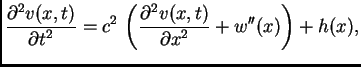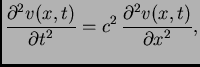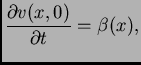Next: Prisilne oscilacije
Up: Slobodne oscilacije žice
Previous: Interpretacija rješenja.
Sadržaj
Indeks
Homogenizacija rubnih uvjeta.
Želimo riješiti problem slobodnih oscilacija žice uz zadane
nehomogene rubne uvjete.
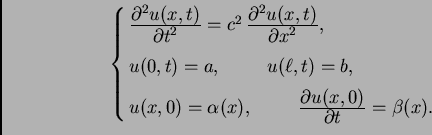 |
(2.26) |
Najprije homogeniziramo rubne uvjete kao u 2.3.3. Na taj
način homogeniziramo rubne uvjete, ali se pojavi nehomogena
diferencijalna jednadžba
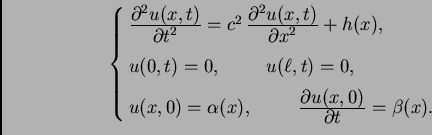 |
(2.27) |
Sada homogeniziramo jednadžbu na sljedeći način.
Rješenje pretpostavljamo u obliku
gdje je 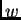 rješenje stacionarnog rubnog problema
Uvrstimo
rješenje stacionarnog rubnog problema
Uvrstimo 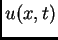 u jednadžbu. Budući da
u jednadžbu. Budući da 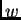 ne ovisi o
ne ovisi o 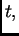 imamo
jer je
imamo
jer je
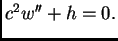
Rubni uvjeti ostaju isti, a početni uvjeti se mijenjaju
pa je tako početni položaj
a početna brzina ostaje
jer
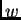 ne ovisi o
ne ovisi o 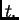 Tako smo problem sveli na homogenu jednadžbu i
homogene rubne uvjete, što smo već riješili.
Tako smo problem sveli na homogenu jednadžbu i
homogene rubne uvjete, što smo već riješili.





Next: Prisilne oscilacije
Up: Slobodne oscilacije žice
Previous: Interpretacija rješenja.
Sadržaj
Indeks
2001-10-26