 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
| Helena Halas, Ema Jurkin (hhalas@grad.hr, ejurkin@rgn.hr)
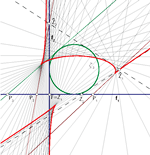
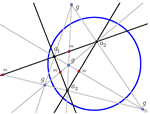
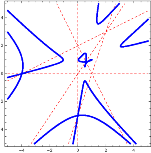
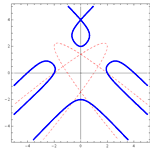
Cirkularne krivulje 3. razreda u kvazihiperboličnoj ravnini dobivene projektivnim preslikavanjemU kvazihiperboličnoj ravnini metrika je inducirana s apsolutnom figurom FQH = {F, f1, f2} koja se sastoji od dva
realna pravca f1 i f2 sa sjecištem u realnoj točki F. Za
krivulju razreda n kažemo da je cirkularna u kvazihiperboličnoj ravnini ako sadrži barem jedan apsolutni pravac.
Krivulje 3. razreda se mogu dobiti projektivnim pridruživanjem između pramena krivulja 2. razreda i niza točaka.
U ovom ćemo članku pokazati kako se svi tipovi cirkularnih krivulja 3. razreda mogu konstruirati projektivnim
preslikavanjem. |
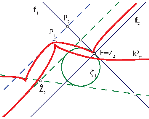
| Ana Sliepčević, Ivana Božić Dragun (ivana.bozic@tvz.hr, anasliepcevic@gmail.com)
Uvod u planimetriju kvazieliptičke ravnineKvazieliptička ravnina jedna je od devet projektivno metričkih ravnina. Apsolutnu figuru FQE = { j1, j2,F} određuju dva imaginarna pravca j1 i j2 i njihovo realno sjecište F. U ovom radu definirat ćemo osnove pojmove, prikazati odabrane konstrukcije i dokazati jedan teorem.Ključne riječi: kvazieliptička ravnina, okomite točke, centrala, klasifikacija qe-konika, hiperoskulacijska qe- kružnica, omotaljka centrala  Article in PDF. Article in PDF. |
|
| Nguyen Le, N J Wildberger (nguyenlecm2009@gmail.com, n.wildberger@unsw.edu.au)
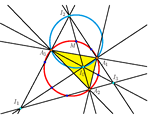
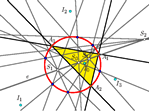
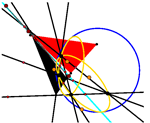
"Upisana simetrija", Eulerovi pravci i Schifflerove točkeProučavamo četverostruku simetriju određenu četverovrhom, čiji su vrhovi središta upisanih (pripisanih) kružnica danog trokuta, te vezu s opisanom
kružnicom trokuta koja je u ovom slučaju konika devet
točaka spomenutog četverokuta. Proučavajući Eulerove
pravce takozvanih upisanih trokuta, pokazujemo da je
poopćenje klasičcne Schifflerove točke skup od četiriju
točaka koje leže na Eulerovom pravcu. Promatra se
četverokut u čijim se vrhovima sijeku Eulerovi pravci
upisanih trokuta, te njegov dijagonalni trokut. Kako se
koristi algebarski pristup, dobiveni rezultati vrijede za
opću bilinearnu formu. Dajemo i primjer svojevrsnog
nestanka četverostruke simetrije. |
|
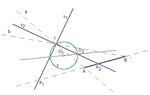
| Gunter Weiss (weissgunter@hotmail.com)
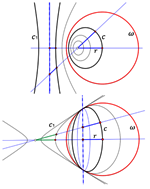
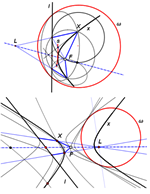
Specijalne konike u hiperboličnoj ravniniU euklidskoj ravnini s obzirom na euklidsku grupu simetrija razlikujemo tri tipa specijalnih konika: kružnice, parabole i specijalne hiperbole. S jedne strane, one imaju specijalno euklidsko svojstvo (vidi [7]), a s druge su strane čvrsto vezane uz apsolutnu eliptičnu involuciju na idealnom pravcu projektivno proširene euklidske ravnine. Zbog toga, u hiperboličnoj ravnini (h-ravnini) - i slično u svakoj Cayley-Kleinovoj ravnini - treba promatrati i projektivna geometrijska svojstva i elementarno-hiperbolična geometrijska svojstva. Pokazuje se da u brojnim slučajevima konika u hiperboličnoj ravnini klasični koncepti "kružnica", "parabola" i "(jednakostranična) hiperbola" nisu primjenjivi (vidi npr. [10]). Unatoč tome, moguće je sustavno promatranje konika u h-ravnini koje imaju jedno ili više svojstava triju euklidskih specijalnih konika. Proučavanje će se vršiti na "univerzalnoj hiperboličnoj ravnini" π, tj. projektivnoj ravnini u kojoj su udaljenost i mjera kuta definirani apsolutnim polaritetom. |
|
| Sebastian Blefari, N J Wildberger (sebastian.eduard.blefari@gmail.com, n.wildberger@unsw.edu.au)
Težišta četverokuta u univerzalnoj hiperboličkoj geometrijiPromatramo veze između osam projektivnih težišta četverokuta u univerzalnoj hiperboličnoj geometriji koji su analogoni baricentričnom središtu euklidskog četverokuta. Određujemo teoretske uvjete postojanja tih središta i pokazujemo da osam težišta tvore dva četverokuta koji zajedno s danim četverokutom imaju trostruku perspektivnu simetriju. I dijagonalni trokuti ovih četverokuta su trostruko perspektivni.
|
|
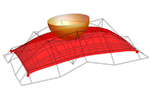
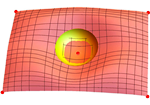
| Boris Odenhal (boris.odehnal@uni-ak.ac.at)
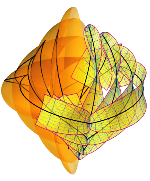
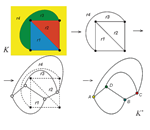
O algebarskim minimalnim plohamaDajemo pregled različitih konstrukcija algebarskih minimalnih ploha u euklidskom trodimenzionalnom prostoru. Posebice se promatraju primjeri niskog stupnja. U tu svrhu koristimo različite prikaze koje daje WEIERSTRASS, uključujući takozvanu Björlingovu formulu. LIJEV stari rezultat pokazuje da se evolute prostornih krivulja mogu koristiti za konstruiranje minimalnih ploha s racionalnim parametrizacijama. Mi opisujemo jednoparametarsku familiju racionalnih minimalnih ploha koje diraju ortogonalne hiperboličke paraboloide duž njihovih krivulja s konstantnom Gaussovom zakrivljenošću. Štoviše, nalazimo novu klasu algebarskih i čak racionalno parametrizirajućih minimalnih ploha i nazivamo ih cikloidnim minimalnim plohama.
|
|
| Szilvia B.-S. Béla, Márta Szilvási-Nagy (belus@math.bme.hu, silvasi@math.bme.hu)
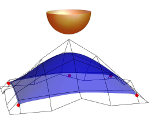
Podešavanje zakrivljenosti B-splajn ploha operacijama na čvor vektorimaNa ovaj način čvor vektori B-splajn ploha određuju
temeljne funkcije zajedno s kontrolnim točkama te oblik plohe. U nekoliko članaka (vidi na primjer [4] i [5])
proučavale su se operacije na čvorovima i njihov utjecaj na obilk krivulja. Izračuni mogu biti izvedeni vrlo
efikasno ako su temeljne funkcije i vektor funkcije B-splajn
plohe prikazane u matričnom obliku (vidi [1] i [6]). U
našem posljednjem radu [2] saželi smo metode operacija
na čvorovima i odgovarajućih izračuna u matričnom obliku.
Također, razvili smo algoritam za izravno klizanje čvorova,
tj. pokazali smo kako čvor može biti premješten u jednom
koraku umjesto da uvodimo novu vrijednost čvora, a zatim
uklanjanjem starog iz čvor vektora.
|
|
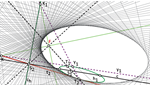
| Mirela Katić-Žlepalo (mkatic@tvz.hr)
Krivulje žarišta u pramenovima konika u pseudo-euklidskoj ravniniU ovom članku pokazat će se da je krivulja žarišta pramena konika u pseudo-euklidskoj ravnini općenito bicirkularna krivulja šestog reda. U nekim slučajevima, u ovisnosti o položaju četiriju temeljnih točaka pramena, krivulja žarišta može biti petog, četvrtog ili trećeg reda, a može biti i konika ili samo pravac.
|
|
| Ivančica Mirošević (ivancica.mirosevic@fesb.hr)
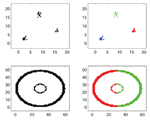
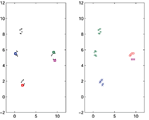
Algoritam k-sredinaU članku je objašnjen algoritam k-sredina (k-means algorithm), heuristika koja rješava NP teški optimizacijski
problem razvrstavanja podataka (točaka) u skupine (klastere) s unaprijed zadanim brojem skupina. Zbog jednostavnosti i brzine konvergencije, algoritam je u
širokoj primjeni, unatoč tendenciji zapinjanja u lokalnom minimumu,
te nemogućosti prepoznavanja skupina koje nisu razdvojive hiperravninama.
|
|
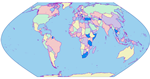
| Mate Glaurdić, Jelena Beban-Brkić, Dražen Tutić (mate.glaurdic@gmail.com, jbeban@geof.hr, dtutic@geof.hr)
O problemu bojanja grafova s primjenom u kartografijiProblem bojanja geografskih političkih karata povijesno je vezan uz teoriju bojanja grafova. Polovicom 19. stoljeća nametnulo se pitanje koliko je boja potrebno da bi se dana geografska karta obojila tako da zemlje koje graniče budu obojane različitim bojama. Do rješenja se došlo povezivanjem karata i grafova. Bilo je potrebno više od jednog stoljeća kako bi se dokazalo da su četiri boje dovoljne za obojiti (geografsku) kartu na takav način da susjedna područja (države) imaju različitu boju.
|