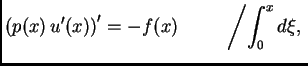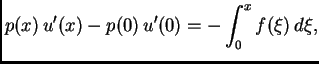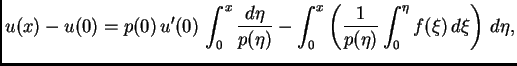Next: I. (Oba uvjeta kinematička.)
Up: Jedinstvenost rješenja
Previous: Jedinstvenost rješenja
Sadržaj
Indeks
Slučaj
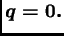 (nema otpora sredstva)
(nema otpora sredstva)
Jednadžba je tada
pa imamo
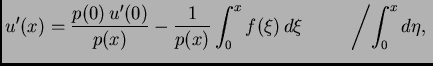 |
(2.10) |
tj.
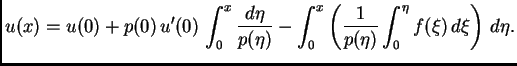 |
(2.11) |
U ovoj formuli imamo dvije neodređene veličine 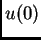 i
i
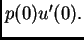 Razmotrimo sada jedinstvenost uz navedene rubne uvjete.
Razmotrimo sada jedinstvenost uz navedene rubne uvjete.
Subsections
2001-10-26