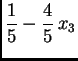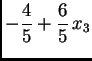Ova diskusija omogućava da se u jednostavnijim slučajevima 'vidi' skup svih rješenja, što je sadržaj sljedećeg primjera.
Primjer 1.20
Razmotrimo ponovno primjer
1.18. U tom slučaju je rang matrice sustava jednak rangu proširene matrice, i iznosi
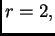
dok je
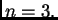
Osim toga je treći stupac linearna kombinacija prva dva. Dakle, svako rješenje je oblika
odnosno
To se može drukčije napisati ovako
što predstavlja parametarske jednadžbe pravca u prostoru. Prvi
stupac desno od jednakosti čine koordinate točke kojom pravac
prolazi, a drugi stupac čine komponente vektora smjera pravca.
Rješenja su dakle točke na pravcu (slika
1.13) u prostoru
(radijvektori u prostoru, čiji vrhovi leže na jednom pravcu).
Rješenje pripadnog homogenog sustava se dobije tako da se izbaci prvi
stupac desno od jednakosti (vektor
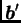
). U tom slučaju su
rješenja točke na pravcu kroz ishodište, koji je paralelan gornjem
pravcu.
Slika 1.13:
Jednoparametarsko rješenje sustava linearnih algebarskih jednadžbi.
|
|
Kako su u gornjem sustavu samo dvije
jednadžbe linearno nezavisne, i budući da svaka od njih predstavlja
jednadžbu ravnine u prostoru, rješavanje ovog sustava se zapravo
svodi na to da se želi dobiti jednadžba pravca u prostoru koji je
zadan kao presjek dviju ravnina.
Primjer 1.21
Ako se sustav sastoji od dvije ili više jednadžbi s tri
nepoznanice, od kojih je samo jedna linearno nezavisna, onda to
znači da su ostale jednadžbe multipli prve. Kako je prva
jednadžba linearna, skup točaka koji je zadovoljava predstavlja
ravninu u prostoru. Dakle, skup svih rješenja takvog sustava je
skup radijvektora (vektorstupaca), čiji vrhovi leže u ravnini u
prostoru koja je zadana bilo kojom od jednadnadžbi sustava (slika
1.14). U pripadnom homogenom sustavu je i dalje samo
jedna (bilo koja) jednadžba linearno nezavisna, pa kao rješenje
homogenog sustava imamo također ravninu, paralelnu prethodnoj, ali
koja prolazi ishodištem.
Slika 1.14:
Dvoparametarsko rješenje sustava linearnih algebarskih jednadžbi.
|
|
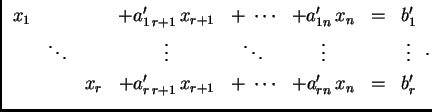
![% latex2html id marker 31748
$\displaystyle \left[\begin{array}{c}
x_1 \\ \vdo...
..._{r+1}-\cdots -a'_{rn}\,x_n \\
x_{r+1} \\ \vdots \\ x_n \end{array}\right]=$](img523.png)
![% latex2html id marker 31750
$\displaystyle = \left[\begin{array}{c}
b'_1 \\ \...
...c}
-a'_{1n} \\ \vdots \\ -a'_{rn} \\ 0 \\ \vdots \\ 1 \end{array}\right].$](img524.png)
![% latex2html id marker 31752
$\displaystyle \boldsymbol{x}= \left[\begin{array}{...
...}
-a'_{1n} \\ \vdots \\ -a'_{rn} \\ 0 \\ \vdots \\ 1
\end{array}\right].$](img525.png)
![% latex2html id marker 31781
$\displaystyle \left[
\begin{array}{c}
x_1 \\ x_...
...eft[
\begin{array}{c}
-\frac{4}{5} \\ \frac{6}{5} \\ 1
\end{array}\right].$](img538.png)