




Next: Točno zaokružene operacije
Up: Još o greškama
Previous: Realni brojevi
Sadržaj
Indeks
U zapisu pomoću pomičnog zareza je
pa je relativna greška
Ako je 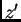 najbolja moguća aproksimacija broja
najbolja moguća aproksimacija broja 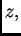 onda je
apsolutna greška (brojnik ovog razlomka) najviše
Brojevi oblika
onda je
apsolutna greška (brojnik ovog razlomka) najviše
Brojevi oblika
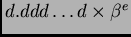 se nalaze između
se nalaze između
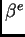 i
i
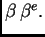 Prema tome najveća moguća
relativna greška je
Ovaj broj se zove kompjuterski epsilon. Najmanja moguća
relativna greška je
Tako je
Prema tome najveća moguća
relativna greška je
Ovaj broj se zove kompjuterski epsilon. Najmanja moguća
relativna greška je
Tako je
Osim relativnom greškom, grešku možemo mjeriti i jedinicom
ulp (units in the last place). Ako
je format
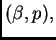 onda se greška u ulpima izražava formulom
onda se greška u ulpima izražava formulom
Primjer 3.24
Neka je format
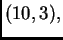
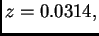
i
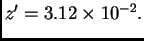
Naći grešku u ulpima.
Rješenje.
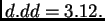 Zatim
Zatim 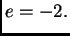 Odatle
Odatle
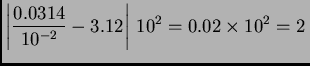
ulpa
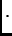
Greška u ulpima omogućava da odredimo broj nepouzdanih znamenki u
približnoj vrijednosti 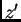 broja
broja 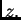 Ako je greška
Ako je greška 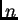 ulpa, onada
je broj nepouzdanih znamenki
ulpa, onada
je broj nepouzdanih znamenki
Primjer 3.25
U formatu
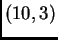
treba izračunati
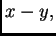
ako je
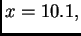
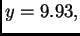
i odrediti broj nepouzdanih znamenki približne
vrijednosti.
Rješenje. Prilikom zbrajanja ili odbijanja manji broj svodimo na potenciju
baze većega, i zatim zbrajamo samo signifikande
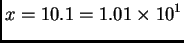
i
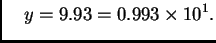
Odatle
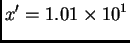
i
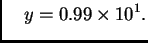
Tako je
dok je točna vrijednost
Greška u ulpima je prema tome
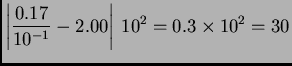
ulpa.
Budući da je
nepouzdane su dvije znamenke.
U ovom primjeru je 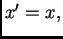 a greška zaokruživanja broja
a greška zaokruživanja broja 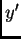 je
je

ulpa.
Dakle u
je jedna znamenka nepouzdana. Ipak prilikom odbijanja se broj
nepouzdanih znamenki povećao. Dapače, kad se odbijaju bliski brojevi
može se dogoditi da niti jedna znamenka u rezultatu nije pouzdana.
Taj problem se može ublažiti tako da se račun izvede s dodatnom
znamenkom (guard digit).
Primjer 3.26
Riješimo primjer
3.25 pomoću dodatne znamenke.
Rješenje. Tada je
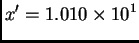
i
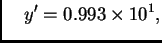
pa je
što je točna vrijednost.
Primjer 3.27
Neka je format
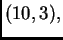
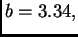
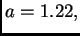
i
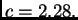
Treba
izračunati
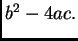
Rješenje.
Dakle greška je
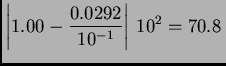
ulpa
Prema tome dvije znamenke su nepouzdane.
Ako se radi s dodatnom znamenkom, greška postaje samo 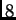 ulpa.
ulpa.
Osim računanjem s dodatnom znamenkom, greška se može umanjiti
rearanžiranjem formule.
Primjer 3.28
Ako je

i
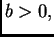
onda je
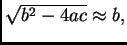
pa formula
sadrži odbijanje bliskih
brojeva, što može dovesti do velike pogreške. U ovom slučaju
možemo racionalizirati brojnik
Primjer 3.29
Heronova formula za računanje površine trokuta glasi
gdje je
Neka je dan trokut takav da je
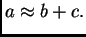
Tada ova formula daje loš rezultat za površinu. Znatno bolja
je formula
Primjer 3.30
Format je
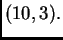
Treba izračunati
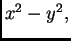
ako je
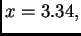
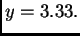
Rješenje. Točan rezultat je
Računanje po formuli
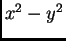
daje
Ovaj račun daje grešku od
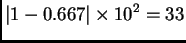
ulpa
No, ako računamo po formuli
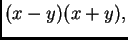
onda imamo
Tako je
što je točan rezultat.
Primjer 3.31
Format je
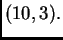
Treba izračunati
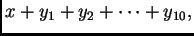
gdje je
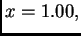
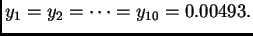
Rješenje. Točan rezultat je
Ako računamo po formuli
onda imamo
jer se prilikom
zbrajanja ili odbijanja brojevi poravnavaju po eksponentu najvećega,
i zatim zaokružuju. Tako imamo
Nakon toga, na isti način
itd. Na kraju imamo
Ako računamo tako da najprije zbrojimo male brojeve, pa zatim dodamo
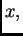 onda imamo
onda imamo
pa je
Odatle
Da se ovaj broj pribroji broju
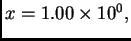
mora ga se svesti na potenciju s eksponentom
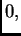
zaokružiti ga i zatim dodati
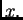
To znači
pa je i





Next: Točno zaokružene operacije
Up: Još o greškama
Previous: Realni brojevi
Sadržaj
Indeks
2001-10-26
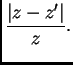
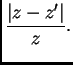
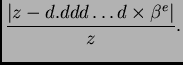
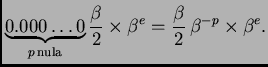
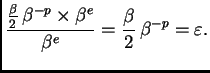
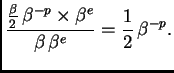
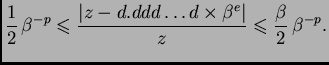
![]() onda se greška u ulpima izražava formulom
onda se greška u ulpima izražava formulom
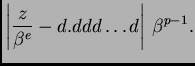
![]() Zatim
Zatim ![]() Odatle
Odatle
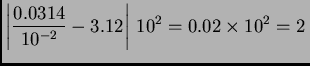 ulpa
ulpa![]() broja
broja ![]() Ako je greška
Ako je greška ![]() ulpa, onada
je broj nepouzdanih znamenki
ulpa, onada
je broj nepouzdanih znamenki
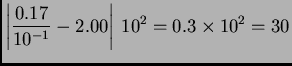 ulpa.
ulpa.
![]() a greška zaokruživanja broja
a greška zaokruživanja broja ![]() je
je
 ulpa.
ulpa.
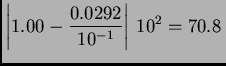 ulpa
ulpa![]() ulpa.
ulpa. 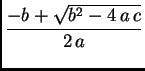
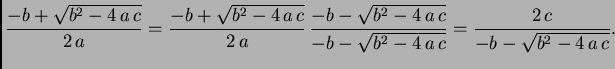
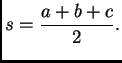
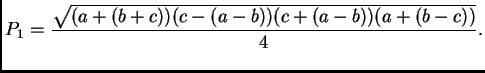
![]() onda imamo
onda imamo