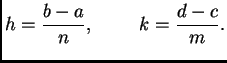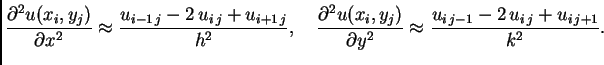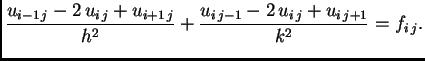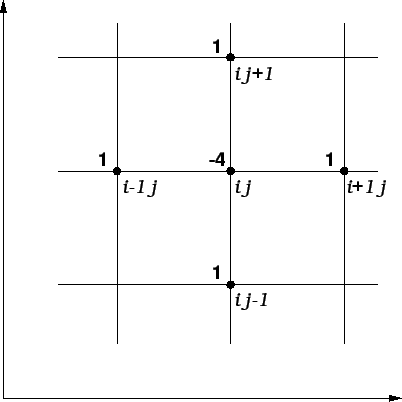Next: Jednadžba provođenja
Up: Metoda konačnih diferencija
Previous: Metoda konačnih diferencija
Sadržaj
Indeks
Jednadžba ravnoteže
Neka je dan rubni problem
gdje je 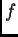 neprekidna funkcija na
neprekidna funkcija na
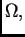 a
a 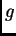 neprekidna na rubu
neprekidna na rubu
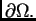
Područje 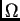 prekrijemo mrežom koju dobijemo tako da segmente
na osi
prekrijemo mrežom koju dobijemo tako da segmente
na osi 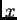 i osi
i osi 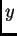 podijelimo ekvidistantno na podsegmenate. Tako
imamo
podijelimo ekvidistantno na podsegmenate. Tako
imamo
Broj 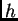 se zove korak mreže po
se zove korak mreže po 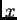 osi, a
osi, a 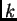 korak
mreže po
korak
mreže po 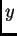 osi. Tako imamo točke podjele
na osima. Točku s koordinatama
zovemo
osi. Tako imamo točke podjele
na osima. Točku s koordinatama
zovemo 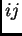 -tim čvorom mreže. Čvor zovemo
unutrašnjim, ako je
-tim čvorom mreže. Čvor zovemo
unutrašnjim, ako je
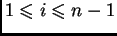 i
i
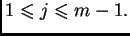 U protivnom kažemo da je čvor
rubni. Stavimo
Kao i u slučaju običnih derivacija, aproksimacije parcijalnih
derivacija možemo dobiti pomoću Taylorove formule za funkcije od
dvije varijable. Tako imamo
Neka je
U protivnom kažemo da je čvor
rubni. Stavimo
Kao i u slučaju običnih derivacija, aproksimacije parcijalnih
derivacija možemo dobiti pomoću Taylorove formule za funkcije od
dvije varijable. Tako imamo
Neka je 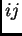 unutrašnji čvor. Tada diferencijalnu jednadžbu u tom
čvoru možemo zamijeniti algebarskom jednadžbom
Ako je čvor
unutrašnji čvor. Tada diferencijalnu jednadžbu u tom
čvoru možemo zamijeniti algebarskom jednadžbom
Ako je čvor 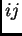 rubni, onda imamo
Time smo dobili onoliko linearnih algebarskih
jednadžbi koliko imamo nepoznanica
rubni, onda imamo
Time smo dobili onoliko linearnih algebarskih
jednadžbi koliko imamo nepoznanica 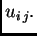 Rješavati treba samo
sustav jednadžbi unutrašnjih čvorova. Pretpostavimo, radi
jednostavnosti, da su
Rješavati treba samo
sustav jednadžbi unutrašnjih čvorova. Pretpostavimo, radi
jednostavnosti, da su
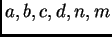 takvi da je
takvi da je 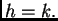 Tada, nakon
množenja s
Tada, nakon
množenja s 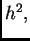 jednadžba
jednadžba 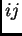 -tog čvora postaje
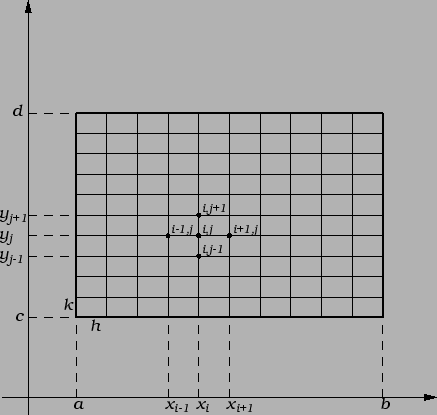
Vidimo da u svakom retku matrice ima najviše pet elemenata
različitih od nule. Na sljedećoj slici su istaknuti oni čvorovi,
čije vrijednosti funkcije
-tog čvora postaje
Vidimo da u svakom retku matrice ima najviše pet elemenata
različitih od nule. Na sljedećoj slici su istaknuti oni čvorovi,
čije vrijednosti funkcije  dolaze u jednadžbi, i upisani su
koeficijenti kojima ih treba množiti.
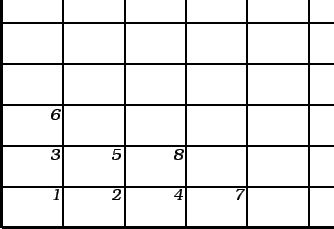
Jednadžbe trebamo na neki način poredati. To možemo učiniti tako
da poredamo čvorove. Njih možemo poredati na različite načine.
Jedan od njih je poredak kao na slici
Dakle
Stavimo
Na taj način dobivamo sljedeći sustav linearnih algebarskih
jednadžbi
dolaze u jednadžbi, i upisani su
koeficijenti kojima ih treba množiti.
Jednadžbe trebamo na neki način poredati. To možemo učiniti tako
da poredamo čvorove. Njih možemo poredati na različite načine.
Jedan od njih je poredak kao na slici
Dakle
Stavimo
Na taj način dobivamo sljedeći sustav linearnih algebarskih
jednadžbi
Prilikom izbora poretka treba paziti na to da matrica dobivenog
sustava jednadžbi bude što uža.





Next: Jednadžba provođenja
Up: Metoda konačnih diferencija
Previous: Metoda konačnih diferencija
Sadržaj
Indeks
2001-10-26
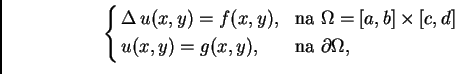
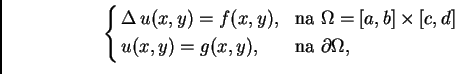
![]() prekrijemo mrežom koju dobijemo tako da segmente
na osi
prekrijemo mrežom koju dobijemo tako da segmente
na osi ![]() i osi
i osi ![]() podijelimo ekvidistantno na podsegmenate. Tako
imamo
podijelimo ekvidistantno na podsegmenate. Tako
imamo