Neka je dana diferencijalna jednadžba
Na temelju Taylorovog teorema srednje vrijednosti imamo
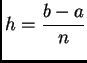
f[x_,y_]=; (* upisuje se f(x,y), ako je jednadzba y'=f(x,y) *)
pocuvj=; (* pocetni uvjet u obliku {x0,y0} *)
kraj=; (* drugi rub segmenta na kojem se trazi rjesenje *)
n=; (* broj podsegmenata podjele *)
h=(kraj-pocuvj[[1]])/n;
x=pocuvj[[1]];
y=pocuvj[[2]];
rj={};
While[x-h<kraj,
rj=Append[rj,{x,y}]//N;
y=y+h f[x,y];
x=x+h];
rj
Rješenje. Lako se vidi da je točno rješenje ![]() U sljedećoj tabeli
imamo približna rješenja dobivena Eulerovom metodom i točna
rješenja zaokružena na devet decimala.
U sljedećoj tabeli
imamo približna rješenja dobivena Eulerovom metodom i točna
rješenja zaokružena na devet decimala.
| 0 | ||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
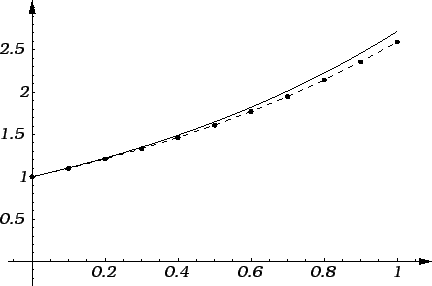
Ova metoda je vrlo jednostavna, ali i vrlo gruba (ocjena pogreške je vrlo gruba) tako da se rijetko kada upotrebljava.