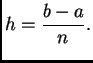Next: Eulerova metoda
Up: Problem početnog uvjeta (Cauchyjev
Previous: Problem početnog uvjeta (Cauchyjev
Sadržaj
Indeks
Želimo riješiti diferencijalnu jednadžbu
na segmentu ![$ [a,b]$](img2579.png) uz početni uvjet
uz početni uvjet
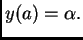 tj. želimo riješiti Cauchyjev problem
tj. želimo riješiti Cauchyjev problem
Metode približnog rješavanja koje ćemo sada opisati osnivaju se na
sljedećoj ideji. Podijelimo segment ![$ [a,b]$](img2579.png) na
na 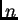 jednakih
dijelova
jednakih
dijelova
Duljina svakog podsegmenta je
Brojeve 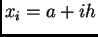 zovemo čvorovima,
a broj
zovemo čvorovima,
a broj 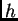 zovemo korakom. Stavimo
Cilj nam je odrediti
zovemo korakom. Stavimo
Cilj nam je odrediti 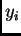 za svaki
za svaki
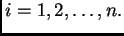 To činimo tako da derivaciju zamijenimo
odgovarajućom algebarskom aproksimacijom, kojom dolazimo do
rekurzivne formule, pomoću koje računamo
To činimo tako da derivaciju zamijenimo
odgovarajućom algebarskom aproksimacijom, kojom dolazimo do
rekurzivne formule, pomoću koje računamo 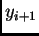 iz poznatog
iz poznatog
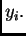 Na taj način, rješenje, koje je neprekidna funkcija,
zamjenjujemo konačnim brojem njezinih vrijednosti. Opisani postupak
se zove diskretizacija. Očekujemo da
će za dovoljno mali
Na taj način, rješenje, koje je neprekidna funkcija,
zamjenjujemo konačnim brojem njezinih vrijednosti. Opisani postupak
se zove diskretizacija. Očekujemo da
će za dovoljno mali 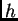 brojevi
brojevi 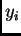 dovoljno dobro aproksimirati
prave vrijednosti funkcije. Važno svojstvo koje diskretizacija treba
imati jeste da s povećanjem
dovoljno dobro aproksimirati
prave vrijednosti funkcije. Važno svojstvo koje diskretizacija treba
imati jeste da s povećanjem 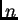 dobivamo sve bolje aproksimacije,
odnosno, preciznije, da brojevi
dobivamo sve bolje aproksimacije,
odnosno, preciznije, da brojevi 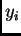 teže prema pravim vrijednostima
funkcije kada
teže prema pravim vrijednostima
funkcije kada
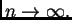





Next: Eulerova metoda
Up: Problem početnog uvjeta (Cauchyjev
Previous: Problem početnog uvjeta (Cauchyjev
Sadržaj
Indeks
2001-10-26
![]() na
na ![]() jednakih
dijelova
jednakih
dijelova