




Next: Jacobijeva OR-metoda (JOR metoda)
Up: Rješavanje sustava jednadžbi
Previous: Gauss-Seidelova metoda
Sadržaj
Indeks
OR (overrelaxation) metode
Navedene metode se mogu poboljšati, obzirom na konvergentnost i
brzinu konvergencije, na sljedeći način.
Matrica 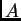 se rastavi kako slijedi
se rastavi kako slijedi
gdje su
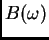 i
i
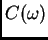 matrice tipa
matrice tipa 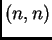 ovisne o
parametru
ovisne o
parametru 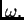 Osim toga
Osim toga
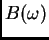 treba biti
regularna. Parametar
treba biti
regularna. Parametar 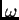 se zove parametar relaksacije. Tada je
se zove parametar relaksacije. Tada je
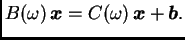 |
(3.12) |
Zbog regularnosti
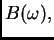 postoji
postoji
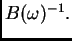 Stavimo
Uvrstimo u (3.12), dobivamo
Iterativni postupak je tada dan formulom
Stavimo
Uvrstimo u (3.12), dobivamo
Iterativni postupak je tada dan formulom
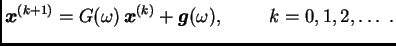 |
(3.13) |
Parametar relaksacije treba odabrati tako da postupak što brže
konvergira.
Subsections
2001-10-26
![]() se rastavi kako slijedi
se rastavi kako slijedi