




Next: Varijacijski račun
Up: Varijacijske metode
Previous: Varijacijske metode
Sadržaj
Indeks
Varijacijski princip
Neka je zadan rubni problem ravnoteže žice
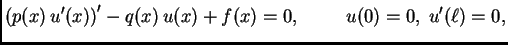 |
(2.30) |
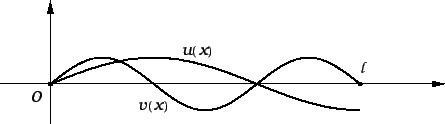
i pretpostavimo da je  ravnotežni položaj. Pretpostavljamo da je
proizvoljni pomak iz položaja ravnoteže žice određen neprekidnom
funkcijom
ravnotežni položaj. Pretpostavljamo da je
proizvoljni pomak iz položaja ravnoteže žice određen neprekidnom
funkcijom 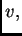 klase
klase
![$ C^1[0,\ell],$](img1804.png) takvom da je
takvom da je 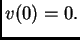 Nazovimo sve takve funkcije dopustivima. Funkciju
Nazovimo sve takve funkcije dopustivima. Funkciju 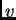 ćemo zvati
perturbacijom ravnotežnog stanja
(položaja). Naglasimo da je
ćemo zvati
perturbacijom ravnotežnog stanja
(položaja). Naglasimo da je 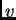 pomak od ravnotežnog stanja a ne
od osi
pomak od ravnotežnog stanja a ne
od osi 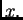 U odnosu na os
U odnosu na os 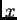 položaj je
položaj je 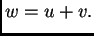 Neka je
Neka je 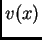 proizvoljna perturbacija (dopustiva funkcija).
Pomnožimo jednadžbu iz (2.31) s
proizvoljna perturbacija (dopustiva funkcija).
Pomnožimo jednadžbu iz (2.31) s 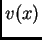 i integrirajmo
duž žice. Dobit ćemo
Parcijalno integrirajmo prvi integral
Zbog
i integrirajmo
duž žice. Dobit ćemo
Parcijalno integrirajmo prvi integral
Zbog
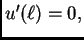 i
i 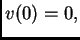 slijedi
slijedi
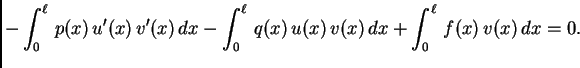 |
(2.31) |
Jednakost (2.32) predstavlja Bernoullijev
princip sačuvanja rada. Prvi član je rad kontaktne sile
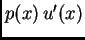 koja se opire deformaciji
koja se opire deformaciji 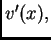 iz
ravnotežnog stanja. Drugi član je rad sile otpora,
a treći rad vanjske sile čija je gustoća
iz
ravnotežnog stanja. Drugi član je rad sile otpora,
a treći rad vanjske sile čija je gustoća 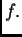 Bernoullijev princip tvrdi da je ukupni rad vanjskih i
unutarnjih sila na perturbaciji ravnotežnog položaja
jednak
Bernoullijev princip tvrdi da je ukupni rad vanjskih i
unutarnjih sila na perturbaciji ravnotežnog položaja
jednak 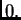 Drugim riječima, ako žicu perturbiramo,
svaki komadić žice prijeđe neki put iz ravnotežnog
stanja. Vanjske sile na tom putu izvrše neki rad. Rad
uslijed sile napetosti žice, koja nastoji vratiti žicu u
ravnotežni položaj jednak je po apsolutnom iznosu radu
vanjskih sila, ali suprotnog predznaka. Tako je suma svih
radova jednaka nuli.
Drugim riječima, ako žicu perturbiramo,
svaki komadić žice prijeđe neki put iz ravnotežnog
stanja. Vanjske sile na tom putu izvrše neki rad. Rad
uslijed sile napetosti žice, koja nastoji vratiti žicu u
ravnotežni položaj jednak je po apsolutnom iznosu radu
vanjskih sila, ali suprotnog predznaka. Tako je suma svih
radova jednaka nuli.
Možemo zaključiti sljedeće. Ako  rješava zadani rubni
problem, onda vrijedi jednakost (2.32) za svaku
dopustivu funkciju (perturbaciju)
rješava zadani rubni
problem, onda vrijedi jednakost (2.32) za svaku
dopustivu funkciju (perturbaciju) 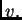
Pretpostavimo da je funkcija  takva da je
takva da je 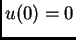 i da zadovoljava
uvjet (Bernoullijev princip)
i da zadovoljava
uvjet (Bernoullijev princip)
za svaku dopustivu funkciju 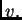 Integrirajmo parcijalno prvi član
na lijevoj strani. Dobivamo
Za dopustivu funkciju
Integrirajmo parcijalno prvi član
na lijevoj strani. Dobivamo
Za dopustivu funkciju 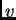 to je, zbog
to je, zbog 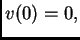
Ovo vrijedi za svaku dopustivu funkciju, pa i takvu za koju
je
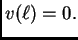 Za takvu
Za takvu  ova jednakost postaje
odnosno
ova jednakost postaje
odnosno
![$\displaystyle \int_0^{\ell}\,\left[\left(p(x)\,u'(x)\right)' - q(x)\,u(x) + f(x)\right]v(x)\,dx = 0.$](img1825.png) |
(2.33) |
Na temelju ove leme zaključujemo da iz 2.35 nužno slijedi
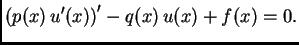 |
(2.34) |
Dakle  zadovoljava diferencijalnu jednadžbu. Po pretpostavci
zadovoljava homogeni kinematički uvjet
zadovoljava diferencijalnu jednadžbu. Po pretpostavci
zadovoljava homogeni kinematički uvjet 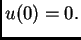 Dokažimo na kraju
da
Dokažimo na kraju
da  zadovoljava i dinamički uvjet
zadovoljava i dinamički uvjet
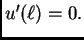 Zbog
(2.36), jednadžba (2.34) se sada svodi na
Kako ona vrijedi za svaku dopustivu funkciju, vrijedi i za
takvu za koju je
Zbog
(2.36), jednadžba (2.34) se sada svodi na
Kako ona vrijedi za svaku dopustivu funkciju, vrijedi i za
takvu za koju je
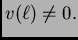 Osim toga je
Osim toga je
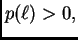 pa
prema tome mora biti
pa
prema tome mora biti
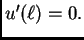
Možemo zaključiti sljedeće. Ako  zadovoljava
Bernoullijev princip, i
zadovoljava
Bernoullijev princip, i 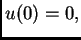 onda
onda  rješava rubni problem
(2.31).
rješava rubni problem
(2.31).
Tako smo dokazali sljedeći teorem.
Primijetimo da se u drugoj tvrdnji zahtijeva od funkcije  samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički
rubni uvjet
samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički
rubni uvjet
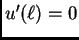 nužno slijedi iz činjenice da
nužno slijedi iz činjenice da  zadovoljava Bernoullijev princip.
zadovoljava Bernoullijev princip.
Promatrajmo i dalje rubni problem (2.37). Stavimo
gdje je  ravnotežni položaj,
ravnotežni položaj, 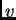 perturbacija, a
perturbacija, a 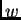 rezultanta. Svakom takvom rezultantnom položaju
rezultanta. Svakom takvom rezultantnom položaju 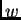 možemo
pridružiti broj
možemo
pridružiti broj
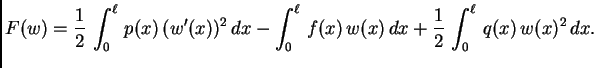 |
(2.37) |
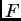 je funkcija koja funkcijama
je funkcija koja funkcijama 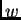 pridružuje brojeve (kao na pr. kod određenog (Riemannovog) integrala). Takva funkcija se zove
funkcional. Prvi integral je unutrašnja
potencijalna energija uslijed deformacije žice, drugi integral je
potencijalna energija vanjske sile, dok je treći integral
potencijalna energija elastične sile otpora. Zato se ovaj funkcional
zove funkcional energije.
Interesira nas čime se odlikuje ravnotežno stanje
pridružuje brojeve (kao na pr. kod određenog (Riemannovog) integrala). Takva funkcija se zove
funkcional. Prvi integral je unutrašnja
potencijalna energija uslijed deformacije žice, drugi integral je
potencijalna energija vanjske sile, dok je treći integral
potencijalna energija elastične sile otpora. Zato se ovaj funkcional
zove funkcional energije.
Interesira nas čime se odlikuje ravnotežno stanje  među svim
mogućim funkcijama
među svim
mogućim funkcijama 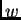 u odnosu na ponašanje funkcionala
u odnosu na ponašanje funkcionala 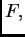 zadanog formulom (2.39).
zadanog formulom (2.39).
Neka je 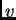 dopustiva funkcija (perturbacija). Podsjetimo da
to znači da je
dopustiva funkcija (perturbacija). Podsjetimo da
to znači da je 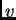 klase
klase
![$ C^1[0,\ell],$](img1804.png) i da je
i da je 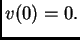 Neka je
Neka je 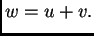 U formulama koje slijede nećemo pisati
varijablu
U formulama koje slijede nećemo pisati
varijablu 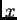 radi kratkoće.
radi kratkoće.
Drugi član je nenegativan zato jer je takva
podintegralna funkcija, a treći je nula zbog Bernoullijevog
principa. Tako imamo
Dakle možemo zaključiti sljedeće. Rezultanta 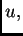 koja predstavlja ravnotežni položaj, se među svim
rezultantama
koja predstavlja ravnotežni položaj, se među svim
rezultantama 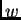 se ističe time da pridaje funkcionalu
se ističe time da pridaje funkcionalu 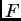 najmanju vrijednost. Za funkciju na kojoj funkcional
najmanju vrijednost. Za funkciju na kojoj funkcional 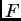 poprima najmanju vrijednost kažemo da minimizira
funkcional
poprima najmanju vrijednost kažemo da minimizira
funkcional 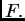 Tako smo dokazali prvu tvrdnju sljedećeg
teorema.
Tako smo dokazali prvu tvrdnju sljedećeg
teorema.
Teorem 18
(Varijacijski princip,
Dirichletov princip)
- Neka je funkcija
![$ u \in C^2[0,\ell]$](img1850.png) rješenje rubnog problema
(2.37). Tada
rješenje rubnog problema
(2.37). Tada  minimizira funkcional
minimizira funkcional 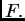
- Neka je funkcija
![$ u \in
C^2[0,\ell],$](img1852.png) neka je
neka je 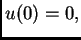 i
neka
i
neka  minimizira funkcional
minimizira funkcional 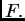 Tada je
Tada je  rješenje rubnog
problema (2.37).
rješenje rubnog
problema (2.37).
Dokažimo drugu tvrdnju (obrat prve). Pretpostavimo da  minimizira
funkcional
minimizira
funkcional 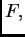 tj. da je
tj. da je
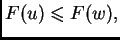 za proizvoljnu
rezultantu
za proizvoljnu
rezultantu 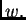 Stavimo
Stavimo
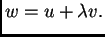 To smijemo, jer ako je
To smijemo, jer ako je 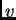 dopustiva funkcija, onda je i
dopustiva funkcija, onda je i
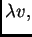 za proizvoljan
za proizvoljan
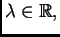 dopustiva.
dopustiva.
Tako vidimo da je 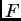 polinom
drugog stupnja u varijabli
polinom
drugog stupnja u varijabli 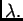 Graf polinoma drugog stupnja je
parabola. Kako je koeficijent uz
Graf polinoma drugog stupnja je
parabola. Kako je koeficijent uz 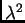 pozitivan parabola ima u
svom tjemenu minimum. Apscisa tjemena je
pozitivan parabola ima u
svom tjemenu minimum. Apscisa tjemena je
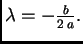 Da bi se minimum dogodio za
Da bi se minimum dogodio za
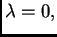 što se mora desiti jer smo
pretpostavili da je
što se mora desiti jer smo
pretpostavili da je
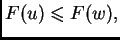 mora nužno biti
mora nužno biti 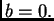 To
znači da mora biti
Dopustiva funkcija
To
znači da mora biti
Dopustiva funkcija 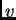 je bila proizvoljna, pa prema tome ova jednakost vrijedi za svaku
dopustivu funkciju
je bila proizvoljna, pa prema tome ova jednakost vrijedi za svaku
dopustivu funkciju 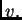 Osim toga pretpostavka je da je
Osim toga pretpostavka je da je 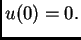 Odatle, po Bernoullijevom principu slijedi da
Odatle, po Bernoullijevom principu slijedi da  rješava rubni
problem (2.37).
rješava rubni
problem (2.37).
Primijetimo na kraju da teorem 18 izražava poznati
mehanički princip: ravnotežno stanje fizikalnog sustava je ono
stanje u kojem je njegova potencijalna energija minimalna.





Next: Varijacijski račun
Up: Varijacijske metode
Previous: Varijacijske metode
Sadržaj
Indeks
2001-10-26

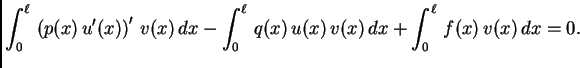
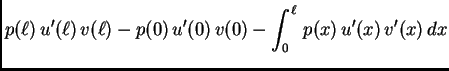
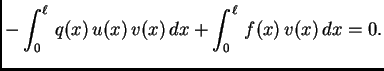
![]() rješava zadani rubni
problem, onda vrijedi jednakost (2.32) za svaku
dopustivu funkciju (perturbaciju)
rješava zadani rubni
problem, onda vrijedi jednakost (2.32) za svaku
dopustivu funkciju (perturbaciju) ![]()
![]() takva da je
takva da je ![]() i da zadovoljava
uvjet (Bernoullijev princip)
i da zadovoljava
uvjet (Bernoullijev princip)
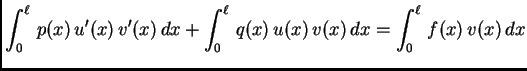
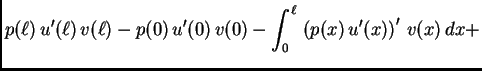
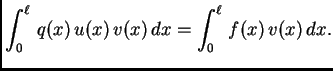
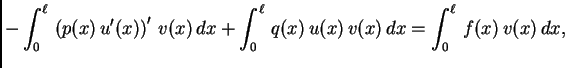
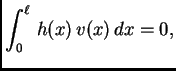
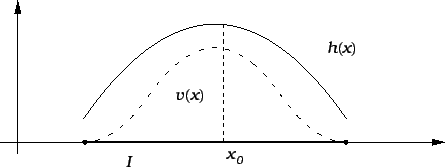
![]() onda zbog
neprekidnosti funkcije
onda zbog
neprekidnosti funkcije ![]() postoji točka
postoji točka
![]() blizu točke
blizu točke ![]() takva da je
takva da je ![]() Isto
možemo zaključiti i za desni rub
Isto
možemo zaključiti i za desni rub ![]() Odatle slijedi da je
dovoljno dokazati tvrdnju leme za
Odatle slijedi da je
dovoljno dokazati tvrdnju leme za
![]()
![]() takav da je
takav da je ![]() Tada, zbog neprekidnosti
funkcije
Tada, zbog neprekidnosti
funkcije ![]() postoji interval
postoji interval ![]() oko točke
oko točke ![]() takav da je
takav da je
![]() za svaki
za svaki ![]() Izaberimo neprekidnu funkciju
Izaberimo neprekidnu funkciju ![]() tako
da je
tako
da je ![]() za svaki
za svaki
![]() i da je
i da je ![]() za svaki
za svaki ![]()
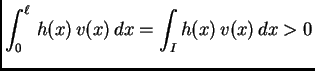
![]() zadovoljava
Bernoullijev princip, i
zadovoljava
Bernoullijev princip, i ![]() onda
onda ![]() rješava rubni problem
(2.31).
rješava rubni problem
(2.31).
![]() samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički
rubni uvjet
samo
zadovoljavanje kinematičkog rubnog uvjeta, dok dinamički
rubni uvjet
![]() nužno slijedi iz činjenice da
nužno slijedi iz činjenice da ![]() zadovoljava Bernoullijev princip.
zadovoljava Bernoullijev princip.
![]() dopustiva funkcija (perturbacija). Podsjetimo da
to znači da je
dopustiva funkcija (perturbacija). Podsjetimo da
to znači da je ![]() klase
klase
![]() i da je
i da je ![]() Neka je
Neka je ![]() U formulama koje slijede nećemo pisati
varijablu
U formulama koje slijede nećemo pisati
varijablu ![]() radi kratkoće.
radi kratkoće. 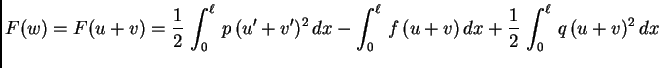
![$\displaystyle = \frac{1}{2}\,\int_0^{\ell}\,p\,\left[u'\,^2+ 2\,u'\,v' + v'\,^2...
...right]\,dx + \frac{1}{2}\,\int_0^{\ell}\,q\,\left[u^2+ 2\,u\,v + v^2\right]\,dx$](img1859.png)
![$\displaystyle = \underbrace{\frac{1}{2}\,\int_0^{\ell}\,p\,u'\,^2\,dx - \int_0^...
...{\frac{1}{2}\,\int_0^{\ell}\,\left[p\,v'\,^2 + q\,v^2\right]\,dx}_{\geqslant 0}$](img1860.png)
![$\displaystyle + \underbrace{\int_0^{\ell}\, \left[p\,u'\,v' + q\,u\,v - f\,v\right]\,dx}_{=0}.$](img1861.png)
![]() koja predstavlja ravnotežni položaj, se među svim
rezultantama
koja predstavlja ravnotežni položaj, se među svim
rezultantama ![]() se ističe time da pridaje funkcionalu
se ističe time da pridaje funkcionalu ![]() najmanju vrijednost. Za funkciju na kojoj funkcional
najmanju vrijednost. Za funkciju na kojoj funkcional ![]() poprima najmanju vrijednost kažemo da minimizira
funkcional
poprima najmanju vrijednost kažemo da minimizira
funkcional ![]() Tako smo dokazali prvu tvrdnju sljedećeg
teorema.
Tako smo dokazali prvu tvrdnju sljedećeg
teorema.
![]() minimizira
funkcional
minimizira
funkcional ![]() tj. da je
tj. da je
![]() za proizvoljnu
rezultantu
za proizvoljnu
rezultantu ![]() Stavimo
Stavimo
![]() To smijemo, jer ako je
To smijemo, jer ako je ![]() dopustiva funkcija, onda je i
dopustiva funkcija, onda je i
![]() za proizvoljan
za proizvoljan
![]() dopustiva.
dopustiva.
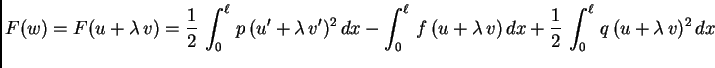
![$\displaystyle = \frac{1}{2}\,\int_0^{\ell}\,p\,\left[u'\,^2+
2\,u'\,\lambda\,v...
...da^2\,v'\,^2\right]\,dx - \int_0^{\ell}\,\left[f\,u
+ f\,\lambda\,v\right]\,dx$](img1870.png)
![$\displaystyle + \frac{1}{2}\,\int_0^{\ell}\,q\,\left[u^2+
2\,u\,\lambda\,v + \...
...nderbrace{\frac{1}{2}\,\int_0^{\ell}\,\left[p\,v'\,^2 +
q\,v^2\right]\,dx}_{a}$](img1871.png)
![$\displaystyle + \lambda\,\underbrace{\int_0^{\ell}\,\left[p\,u'\,v' +
q\,u\,v ...
...t_0^{\ell}\,
\left[p\,u'\,^2 + q\,u^2\right]\,dx - \int_0^{\ell}\,f\,u\,dx}_{c}$](img1872.png)
![$\displaystyle \int_0^{\ell}\,\left[p\,u'\,v' + q\,u\,v - f\,v\right]\,dx = 0.$](img1879.png)