Ako fiksiramo jednu točku ![]() kao početak svih vektora, onda svakoj
točki
kao početak svih vektora, onda svakoj
točki ![]() pripada jedan i samo jedan vektor
pripada jedan i samo jedan vektor
![]() . Vektor
. Vektor
![]() se zove radijvektor.
se zove radijvektor.
Ako se točke ![]() biraju na pravcu
biraju na pravcu ![]() kroz
kroz ![]() onda se skup svih takvih
radijvektora označava
onda se skup svih takvih
radijvektora označava
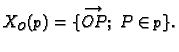
Ako se točke ![]() biraju u ravnini
biraju u ravnini ![]() kroz
kroz ![]() onda se skup svih takvih
radijvektora označava
onda se skup svih takvih
radijvektora označava
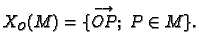
Ako se točke ![]() biraju u prostoru
biraju u prostoru ![]() , onda se skup svih takvih
radijvektora označava
, onda se skup svih takvih
radijvektora označava
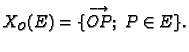
Obzirom da je u
![]() dano zbrajanje i množenje sa
skalarom s onih osam svojstava,
dano zbrajanje i množenje sa
skalarom s onih osam svojstava, ![]() zovemo vektorskim prostorom
svih radijvektora na pravcu
zovemo vektorskim prostorom
svih radijvektora na pravcu ![]() ,
, ![]() zovemo vektorskim prostorom
svih radijvektora u ravnini
zovemo vektorskim prostorom
svih radijvektora u ravnini ![]() ,
, ![]() zovemo vektorskim prostorom
svih radijvektora u prostoru
zovemo vektorskim prostorom
svih radijvektora u prostoru ![]() .
.