




Next: Vektorski prostor radijvektora
Up: Dodaci
Previous: Skup kompleksnih brojeva
Contents
Index
Supremum i infimum
Definicija 52
Neka je
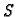
neprazan skup u
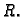
Za realan broj
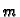
kažemo da je
infimum skupa
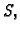
ako vrijedi
- 1.
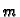 je minoranta, tj.
je minoranta, tj.
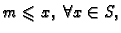
- 2.
- za svaki
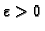 postoji
postoji 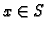 takav, da je
takav, da je
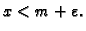
U tom slučaju pišemo
Za realan broj
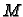
kažemo da je
supremum skupa
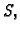
ako vrijedi
- 1.
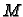 je majoranta, tj.
je majoranta, tj.
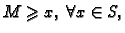
- 2.
- za svaki
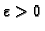 postoji
postoji 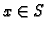 takav, da je
takav, da je
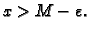
U tom slučaju pišemo
Slobodnije govoreći možemo reći da je supremum najmanja majoranta, a
infimum najveća minoranta nepraznog skupa.
Osnovno svojstvo skupa realnih brojeva predstavlja sljedeća tvrdnja.
Teorem 41
Svaki neprazan, odozgo ograničen skup u
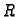
ima supremum. Svaki
neprazan, odozdo ograničen skup u
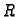
ima infimum.
Primjer 8.4
Interval
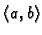
ima infimum
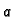
i supremum
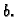
Rješenje. Doista,
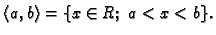 Odatle
slijedi da je
Odatle
slijedi da je 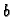 majoranta. Za proizvoljan
majoranta. Za proizvoljan
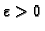 vrijedi
vrijedi
osim toga
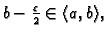
dakle
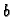
je
supremum.
Primjer 8.5
Skup
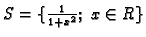
ima infimum 0 i
supremum
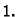
Rješenje. Za svaki 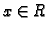 očito vrijedi
očito vrijedi
tj. 0 je minoranta, a
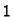
je majoranta skupa
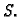
Dokažimo najprije
da je
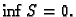
Uzmimo
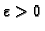
proizvoljan. Nejednadžba
ima, za
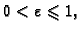
rješenja u skupu
a za
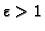
rješenje je bilo koji realan broj. Prema tome niti
jedan
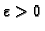
nije minoranta. Slijedi da je 0 najveća
minoranta, tj. infimum.
Dokažimo sada da je 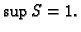 Uzmimo
Uzmimo
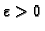 proizvoljan.
Nejednadžba
proizvoljan.
Nejednadžba
ima, za
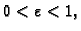
rješenja u skupu
a za
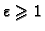
rješenje je bilo koji realan broj. Prema tome
niti jedan broj manji od
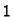
nije majoranta. Slijedi da je
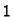
najveća
majoranta, tj. supremum.
Ako skup 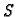 ima supremum
ima supremum 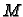 i on pripada skupu
i on pripada skupu 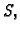 onda se broj
onda se broj 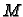 zove maksimum skupa
zove maksimum skupa 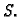 Ako skup
Ako skup 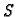 ima infimum
ima infimum
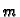 i on pripada skupu
i on pripada skupu 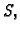 onda se broj
onda se broj 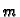 zove
minimum skupa
zove
minimum skupa 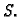
Primjer 8.6
Skup
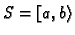
ima minimum
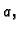
ali nema maksimum.
Rješenje. Doista,
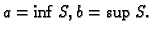 Pri tom
Pri tom
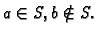
Ako je skup 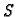 neograničen odozgo, onda nema supremum i to se kraće
zapisuje na sljedeći način
neograničen odozgo, onda nema supremum i to se kraće
zapisuje na sljedeći način
Ako je skup 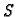 neograničen odozdo, onda nema infimum i to se kraće
zapisuje na sljedeći način
neograničen odozdo, onda nema infimum i to se kraće
zapisuje na sljedeći način





Next: Vektorski prostor radijvektora
Up: Dodaci
Previous: Skup kompleksnih brojeva
Contents
Index
Salih Suljagic
2000-03-11
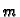 je minoranta, tj.
je minoranta, tj.
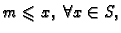
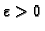 postoji
postoji 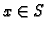 takav, da je
takav, da je
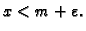
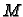 je majoranta, tj.
je majoranta, tj.
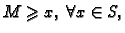
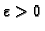 postoji
postoji 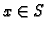 takav, da je
takav, da je
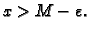
![]() Odatle
slijedi da je
Odatle
slijedi da je ![]() majoranta. Za proizvoljan
majoranta. Za proizvoljan
![]() vrijedi
vrijedi
![]() očito vrijedi
očito vrijedi
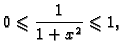
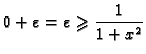
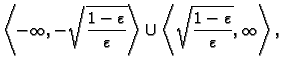
![]() Uzmimo
Uzmimo
![]() proizvoljan.
Nejednadžba
proizvoljan.
Nejednadžba
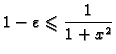
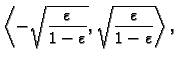
![]() ima supremum
ima supremum ![]() i on pripada skupu
i on pripada skupu ![]() onda se broj
onda se broj ![]() zove maksimum skupa
zove maksimum skupa ![]() Ako skup
Ako skup ![]() ima infimum
ima infimum
![]() i on pripada skupu
i on pripada skupu ![]() onda se broj
onda se broj ![]() zove
minimum skupa
zove
minimum skupa ![]()
![]() Pri tom
Pri tom
![]()
![]() neograničen odozgo, onda nema supremum i to se kraće
zapisuje na sljedeći način
neograničen odozgo, onda nema supremum i to se kraće
zapisuje na sljedeći način
![]() neograničen odozdo, onda nema infimum i to se kraće
zapisuje na sljedeći način
neograničen odozdo, onda nema infimum i to se kraće
zapisuje na sljedeći način