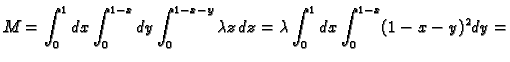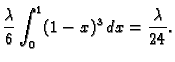Next: Računanje integrala supstitucijom
Up: Višestruki integrali
Previous: Dvostruki integral
Contents
Index
Subsections
Neka materijalno tijelo  zauzima u prostoru područje
zauzima u prostoru područje
![$ K=[a_1,a_2]\times [b_1,b_2]\times [c_1,c_2],$](img1163.gif) koje predstavlja
kvadar sa stranicama paralelnim koordinatnim ravninama. Neka je gustoća
mase tijela
koje predstavlja
kvadar sa stranicama paralelnim koordinatnim ravninama. Neka je gustoća
mase tijela  u točki
u točki
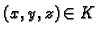 jednaka
jednaka
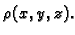 Problem je izračunati masu
Problem je izračunati masu 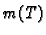 tijela
tijela 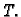
Načinimo
proizvoljne subdivizije segmenata
![$ [a_1,a_2],[b_1,b_2],[c_1,c_2].$](img1167.gif)
Subdivizijama smo kvadar 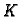 podijelili na manje kvadre
podijelili na manje kvadre
![$ K_{ijk}=[x_{i-1},x_i]\times [y_{j-1},y_j]\times [z_{k-1},z_k].$](img1171.gif) Neka je
Tada vrijedi
Tim sumama smo približno odredili masu. Očekujemo da ćemo sa sve
finijim podjelama dobivati sve bolje aproksimacije mase
Neka je
Tada vrijedi
Tim sumama smo približno odredili masu. Očekujemo da ćemo sa sve
finijim podjelama dobivati sve bolje aproksimacije mase 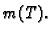 Ova
konstrukcija nas vodi na pojam trostrukog integrala.
Ova
konstrukcija nas vodi na pojam trostrukog integrala.
Pretpostavimo da je dana ograničena funkcija  na zatvorenom
kvadru
na zatvorenom
kvadru
![$ K=[a_1,a_2]\times [b_1,b_2]\times [c_1,c_2].$](img1176.gif) Podsjetimo se da
ograničenost funkcije znači da je slika funkcije
Podsjetimo se da
ograničenost funkcije znači da je slika funkcije
ograničen skup u 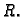 Neka su
subdivizije segmenata
Neka su
subdivizije segmenata
![$ [a_1,a_2],[b_1,b_2],[c_1,c_2].$](img1167.gif) Neka je
Ograničenost funkcije na
Neka je
Ograničenost funkcije na 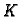 povlači njenu ograničenost na
povlači njenu ograničenost na
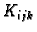 za svaki
za svaki  To znači da postoje supremum i infimum skupa
To znači da postoje supremum i infimum skupa
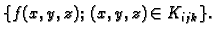 Stavimo
Ako je funkcija
Stavimo
Ako je funkcija  neprekidna na
neprekidna na 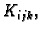 onda se supremum poklapa s
maksimumom, a infimum s minimumom funkcije na
onda se supremum poklapa s
maksimumom, a infimum s minimumom funkcije na 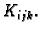
Formirajmo sljedeće sume.
Broj  se zove
donja Darbouxova suma, a broj
se zove
donja Darbouxova suma, a broj  se zove
gornja Darbouxova suma. Neka je
se zove
gornja Darbouxova suma. Neka je
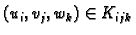 proizvoljan. Broj
se zove
integralna suma. Zbog očigledne nejednakosti
imamo
proizvoljan. Broj
se zove
integralna suma. Zbog očigledne nejednakosti
imamo
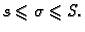 |
(2.3) |
Sve što smo do sada uradili proizašlo je iz jedne subdivizije. Sada
zamislimo sve moguće subdivizije. Svaka od njih daje po jednu donju i
jednu gornju Darbouxovu sumu, i beskonačno mnogo integralnih suma,
ali uvijek vrijedi nejednakost (2.3). Označimo s
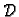 skup svih donjih Darbouxovih suma, a s
skup svih donjih Darbouxovih suma, a s
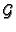 skup svih
gornjih Darbouxovih suma. Neka je
skup svih
gornjih Darbouxovih suma. Neka je
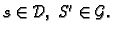 Uzmimo novu subdiviziju, koja sadrži sve točke jedne i druge
subdivizije, i neka su
Uzmimo novu subdiviziju, koja sadrži sve točke jedne i druge
subdivizije, i neka su 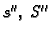 njezina donja i gornja Darbouxova
suma. Tada vrijedi
njezina donja i gornja Darbouxova
suma. Tada vrijedi
Odatle slijedi da je bilo koja donja Darbouxova suma manja ili jednaka
bilo kojoj gornjoj Darbouxovoj sumi. To znači da je skup
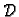 odozgo, a skup
odozgo, a skup
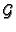 odozdo ograničen, pa prema tome postoje
odozdo ograničen, pa prema tome postoje
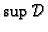 i
i
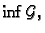 i vrijedi
i vrijedi
Definicija 19
Kažemo da je funkcija
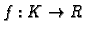 integrabilna
integrabilna ili
Riemann-integrabilna na
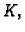
ako je
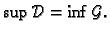
U tom slučaju broj
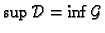
zovemo
trostrukim
integralom funkcije

na
![$ K=[a_1,a_2]\times [b_1,b_2]\times [c_1,c_2].$](img1176.gif)
Pišemo
Funkcija

se zove
podintegralna
funkcija, kvadar
![$ K=[a_1,a_2]\times
[b_1,b_2]\times [c_1,c_2]$](img1193.gif) područje
integracije
područje
integracije.
Nije svaka ograničena funkcija integrabilna, kao što pokazuje
sljedeći primjer.
Primjer 2.4
Neka je
![$ f:[0,1]\times[0,1]\times[0,1]\rightarrow R$](img1194.gif)
funkcija definirana formulom
Ova funkcija nije integrabilna u smislu Riemanna.
Zaista, uzmemo li proizvoljnu subdiviziju, proizvoljni subkvadar sadrži
i točke s racionalnim koordinatama i one druge. To znači da je uvijek
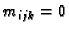 i
i
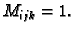 Odatle, za proizvoljnu subdiviziju,
Odatle, za proizvoljnu subdiviziju,
Tako je
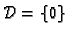
i
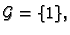
pa je
Neka je  zatvoreno ograničeno područje u
zatvoreno ograničeno područje u 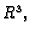 i neka je
i neka je
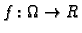 ograničena funkcija. Oko
ograničena funkcija. Oko  opišemo
minimalni kvadar
opišemo
minimalni kvadar
![$ K=[a_1,a_2]\times
[b_1,b_2]\times [c_1,c_2]$](img1193.gif) i
definiramo novu funkciju
i
definiramo novu funkciju
Definicija 20
Kažemo da je
 integrabilna funkcija na
integrabilna funkcija na
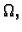
ako je
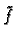
integrabilna na
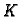
i broj
zovemo
trostrukim integralom
funkcije 
po području
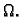
Vratimo se na problem mase. Neka je 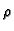 gustoća mase materijalnog
tijela
gustoća mase materijalnog
tijela 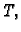 koje u prostoru zauzima područje
koje u prostoru zauzima područje 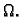 Neka je
Neka je 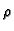 ograničena funkcija na području
ograničena funkcija na području 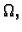 i neka je
i neka je
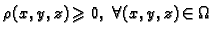 Na temelju do sada
rečenog prirodno je reći da tijelo
Na temelju do sada
rečenog prirodno je reći da tijelo 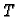 ima masu, ako je
ima masu, ako je
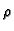 integrabilna na
integrabilna na 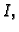 i da je u tom slučaju
masa od
i da je u tom slučaju
masa od 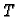 jednaka
jednaka
- 1.
- Ako su
 i
i 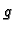 integrabilne funkcije na
integrabilne funkcije na  i
i
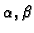 proizvoljni realni brojevi, onda je
proizvoljni realni brojevi, onda je
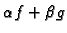 integrabilna na
integrabilna na
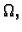 i
i
- 2.
- Ako je
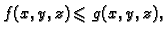 za svaki
za svaki
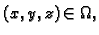 onda je
onda je
- 3.
- Neka je
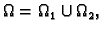 gdje su
gdje su 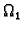 i
i
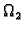 zatvorena područja čiji je presjek ploha (skup
volumena nula). Tada je
zatvorena područja čiji je presjek ploha (skup
volumena nula). Tada je
- 4.
-
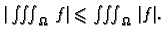
- 5.
- Teorem srednje vrijednosti
(integralni). Neka
je
 neprekidna funkcija integrabilna na zatvorenom
ograničenom području
neprekidna funkcija integrabilna na zatvorenom
ograničenom području 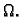 Tada postoji
Tada postoji
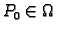 tako da
je
gdje je
tako da
je
gdje je
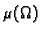 volumen područja
volumen područja 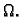
Dokaz. Neprekidna funkcija na zatvorenom
ograničenom području dostiže svoju najmanju i svoju najveću
vrijednost, tj. postoje točke 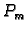 i
i 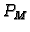 takve da je
za svaki
takve da je
za svaki
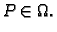 Odatle slijedi
tj.
Osim toga neprekidna funkcija na zatvorenom ograničenom području
dostiže svaku međuvrijednost, što znači da postoji
Odatle slijedi
tj.
Osim toga neprekidna funkcija na zatvorenom ograničenom području
dostiže svaku međuvrijednost, što znači da postoji
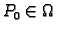 takav da je
takav da je

Pretpostavimo da je  integrabilna na kvadru
integrabilna na kvadru
![$ K=[a_1,a_2]\times [b_1,b_2]\times [c_1,c_2].$](img1176.gif) Kao kod dvostrukog integrala, možemo se
uvjeriti da za bilo koji
Kao kod dvostrukog integrala, možemo se
uvjeriti da za bilo koji
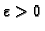 postoji subdivizija takva, da
za svaku pripadnu integralnu sumu
postoji subdivizija takva, da
za svaku pripadnu integralnu sumu 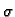 vrijedi
vrijedi
s točnošću
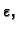 tj. da vrijedi
tj. da vrijedi
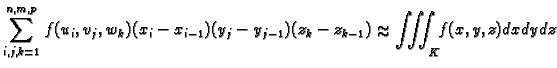 |
(2.4) |
s točnošću
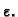
Formulu (2.4) možemo prepisati na više načina. Na
primjer
Na temelju ovih prikaza zaključujemo da vrijede formule
Tako se računanje trostrukog integrala po kvadru svodi na
sukcesivno računanje tri jednostruka integrala. Ako je još
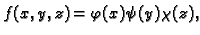 onda se trostruki integral svodi na
produkt tri jednostruka integrala
onda se trostruki integral svodi na
produkt tri jednostruka integrala
Primjer 2.5
Neka je
![$ K=[0,1]\times[0,1]\times[0,1].$](img1225.gif)
Neka je
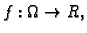 i neka je
i neka je
![$ K=[a_1,a_2]\times
[b_1,b_2]\times [c_1,c_2]$](img1193.gif) minimalni kvadar koji sadrži
minimalni kvadar koji sadrži 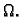 Neka je dalje područje
Neka je dalje područje  takvo da se njegov rub sastoji od dvije plohe, koje su grafovi funkcija od
takvo da se njegov rub sastoji od dvije plohe, koje su grafovi funkcija od
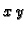 i to donji rub neka je graf funkcije
i to donji rub neka je graf funkcije 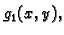 a gornji graf funkcije
a gornji graf funkcije
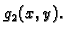
Neka je pravokutnik 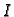 projekcija kvadra
projekcija kvadra 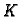 na ravninu
na ravninu 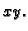 Tada je
Dvostruki integral, koji je ostao izvan zagrada se može računati kao
što je ranije objašnjeno. Tako imamo
gdje su
Tada je
Dvostruki integral, koji je ostao izvan zagrada se može računati kao
što je ranije objašnjeno. Tako imamo
gdje su 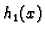 i
i 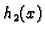 funkcije, čiji grafovi čine rub područja u
ravnini
funkcije, čiji grafovi čine rub područja u
ravnini 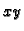 koje se dobije kad se tijelo
koje se dobije kad se tijelo 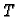 projicira na ravninu
projicira na ravninu 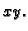
Ako za neko područje nije moguće gornji i donji rub shvatiti kao
grafove funkcija, onda ga podijelimo na manja područja koja imaju to
svojstvo.
Trostruki integral se može koristiti za izračunavanje volumena
tijela. Ako nad tijelom  integriramo funkciju
integriramo funkciju
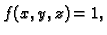 onda time računamo masu tijela, čija je gustoća mase
onda time računamo masu tijela, čija je gustoća mase 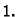 Tako je
masa brojčano jednaka volumenu tijela, tj.
Tako je
masa brojčano jednaka volumenu tijela, tj.
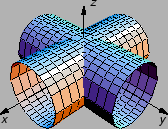
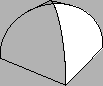
Primjer 2.6
Naći volumen tijela što ga određuje presjek dva valjka
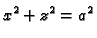
i
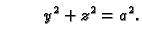
Slika:
Na lijevoj slici su zadani valjci, a na desnoj je onaj dio njihovog presjeka, koji se nalazi iznad ravnine 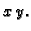
|
|
Rješenje.
- 1.
- Koji problem rješava trostruki integral?
- 2.
- Koje su osnovne pretpostavke na funkciju i na područje da bi se
uopće moglo govoriti o trostrukom integralu?
- 3.
- Kako se definira trostruki integral po kvadru čije su stranice
paralelne koordinatnim ravninama?
- 4.
- Što su to donja, gornja Darbouxova suma i integralna suma?
- 5.
- Kad kažemo za neku funkciju da je integrabilna na nekom području?
- 6.
- Da li je svaka ograničena funkcija integrabilana?
- 7.
- Kako se definira trostruki integral po proizvoljnom zatvorenom
ograničenom području?
- 8.
- Navedite svojstva trostrukog integrala.
- 9.
- Kako glasi teorem srednje vrijednosti za trostruke integrale? Da
li ga znate dokazati?
- 10.
- Kako se računa trostruki integral po kvadru? Objasnite zašto.
- 11.
- Kako se računa trostruki integral po proizvoljnom području?
- 12.
- Da li se pomoću trostrukog integrala može računati volumen?
- 1.
- Treba izračunati
gdje je
 područje omeđeno plohama
područje omeđeno plohama
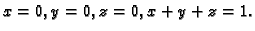
Rješenje.
- 2.
-
- 3.
- Naći masu tijela omeđenog plohama
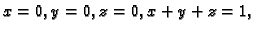 ako je
gustoća mase proporcionalna udaljenosti od osi
ako je
gustoća mase proporcionalna udaljenosti od osi 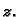
Rješenje. Gustoća je
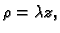 pa je
pa je





Next: Računanje integrala supstitucijom
Up: Višestruki integrali
Previous: Dvostruki integral
Contents
Index
Salih Suljagic
2000-03-11
![]() zauzima u prostoru područje
zauzima u prostoru područje
![]() koje predstavlja
kvadar sa stranicama paralelnim koordinatnim ravninama. Neka je gustoća
mase tijela
koje predstavlja
kvadar sa stranicama paralelnim koordinatnim ravninama. Neka je gustoća
mase tijela ![]() u točki
u točki
![]() jednaka
jednaka
![]() Problem je izračunati masu
Problem je izračunati masu ![]() tijela
tijela ![]()
![]()
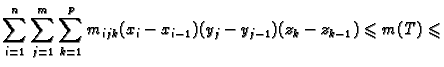
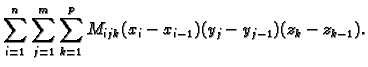
![]() na zatvorenom
kvadru
na zatvorenom
kvadru
![]() Podsjetimo se da
ograničenost funkcije znači da je slika funkcije
Podsjetimo se da
ograničenost funkcije znači da je slika funkcije
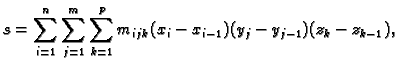
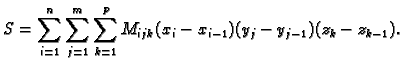
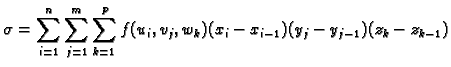
![]() skup svih donjih Darbouxovih suma, a s
skup svih donjih Darbouxovih suma, a s
![]() skup svih
gornjih Darbouxovih suma. Neka je
skup svih
gornjih Darbouxovih suma. Neka je
![]() Uzmimo novu subdiviziju, koja sadrži sve točke jedne i druge
subdivizije, i neka su
Uzmimo novu subdiviziju, koja sadrži sve točke jedne i druge
subdivizije, i neka su ![]() njezina donja i gornja Darbouxova
suma. Tada vrijedi
njezina donja i gornja Darbouxova
suma. Tada vrijedi
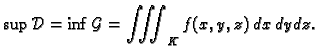
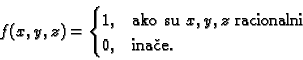
![]() i
i
![]() Odatle, za proizvoljnu subdiviziju,
Odatle, za proizvoljnu subdiviziju,
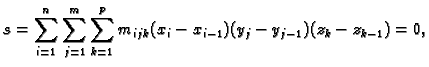
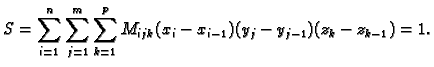
![]() zatvoreno ograničeno područje u
zatvoreno ograničeno područje u ![]() i neka je
i neka je
![]() ograničena funkcija. Oko
ograničena funkcija. Oko ![]() opišemo
minimalni kvadar
opišemo
minimalni kvadar
![]() i
definiramo novu funkciju
i
definiramo novu funkciju
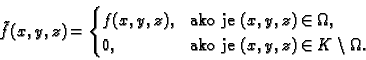
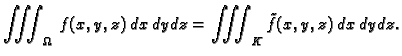
![]() gustoća mase materijalnog
tijela
gustoća mase materijalnog
tijela ![]() koje u prostoru zauzima područje
koje u prostoru zauzima područje ![]() Neka je
Neka je ![]() ograničena funkcija na području
ograničena funkcija na području ![]() i neka je
i neka je
![]() Na temelju do sada
rečenog prirodno je reći da tijelo
Na temelju do sada
rečenog prirodno je reći da tijelo ![]() ima masu, ako je
ima masu, ako je
![]() integrabilna na
integrabilna na ![]() i da je u tom slučaju
masa od
i da je u tom slučaju
masa od ![]() jednaka
jednaka
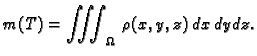
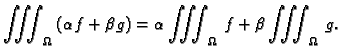
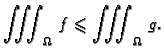
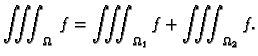
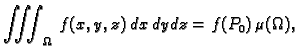
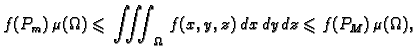
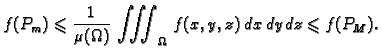
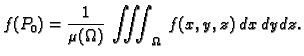
![]() integrabilna na kvadru
integrabilna na kvadru
![]() Kao kod dvostrukog integrala, možemo se
uvjeriti da za bilo koji
Kao kod dvostrukog integrala, možemo se
uvjeriti da za bilo koji
![]() postoji subdivizija takva, da
za svaku pripadnu integralnu sumu
postoji subdivizija takva, da
za svaku pripadnu integralnu sumu ![]() vrijedi
vrijedi
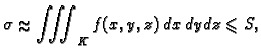
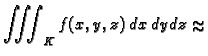
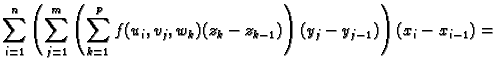
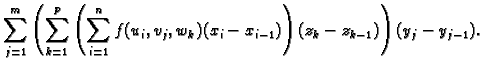
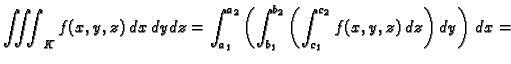
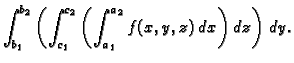
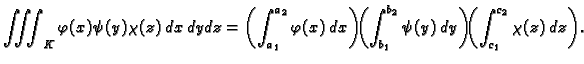
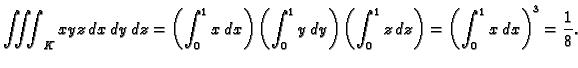
![]() i neka je
i neka je
![]() minimalni kvadar koji sadrži
minimalni kvadar koji sadrži ![]() Neka je dalje područje
Neka je dalje područje ![]() takvo da se njegov rub sastoji od dvije plohe, koje su grafovi funkcija od
takvo da se njegov rub sastoji od dvije plohe, koje su grafovi funkcija od
![]() i to donji rub neka je graf funkcije
i to donji rub neka je graf funkcije ![]() a gornji graf funkcije
a gornji graf funkcije
![]()

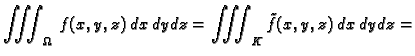
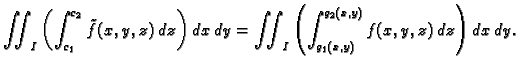
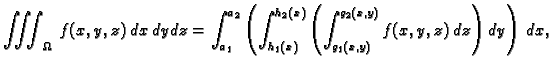
![]() integriramo funkciju
integriramo funkciju
![]() onda time računamo masu tijela, čija je gustoća mase
onda time računamo masu tijela, čija je gustoća mase ![]() Tako je
masa brojčano jednaka volumenu tijela, tj.
Tako je
masa brojčano jednaka volumenu tijela, tj.
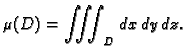
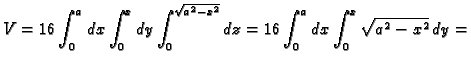
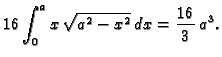
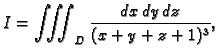
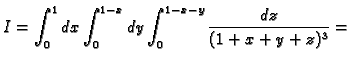
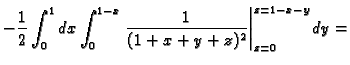
![$\displaystyle -\frac{1}{2}\int_0^1dx\int_0^{1-x}
\left[\frac{1}{4}-\frac{1}{(1+...
...frac{1}{2}\int_0^1
\left[\frac{1}{4}y+\frac{1}{1+x+y}\right]_{y=0}^{y=1-x}\,dx=$](img1247.gif)
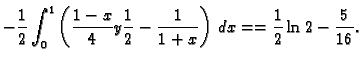
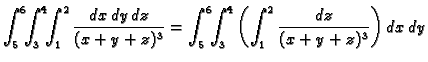
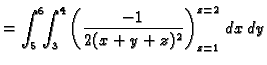
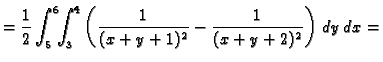
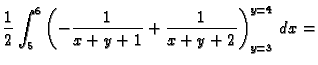
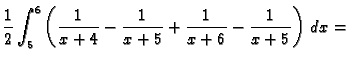
![$\displaystyle \frac{1}{2}\left[\ln\vert x+4\vert-\ln\vert x+5\vert+\ln\vert x+6\vert-\ln\vert x+5\vert\right]_{x=5}^{x=6}=
\frac{1}{2}\ln \frac{4000}{3993}.$](img1254.gif)
![]() pa je
pa je