Sažetci

Znanstveno-stručni časopis
Hrvatskog društva za geometriju i grafiku

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics

	In Memoriam Akademik Stanko Bilinski (1909. -1998.) ...Svojim dugim i plodnim znanstvenim, stručnim i nastavničkim radom profesor Bilinski podario je mnogo i mnogima, onima koji su toga svjesni već odavno, onima koji će to tek biti, i onima koji to neće ni znati. Bio je zaljubljenik u geometriju, njezin štovatelj i vrstan znalac, ali također vješt graditelj i uspješan prinositelj. Sjećajući se voljenog profesora i učitelja, cijenjenoga kolege i međunarodno priznatog znanstvenika, dragog prijatelja, te uvijek gospodina, ostajemo mu zahvalni i vjerni onomu o čemu nas je učio, izravno i neizravno, kao matematičar i povrh svega kao čovjek. Mirko Polonijo Članak u PDF-u.

	Zdravka Božikov (bozikov@cigla.gradst.hr) O simetričnim dizajnima s parametrima (101, 25, 6) Poznat je samo jedan simetrični dizajn s parametrima (101, 25, 6) koji ima Singerovu grupu (vidi [3]). U ovom radu pokušavamo konstruirati takav dizajn bez Singerove grupe. Ključne riječi: simetrični dizajn, automorfizam, Frobeniusova grupa, orbitna struktura Članak u PDF-u.

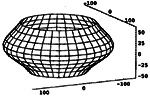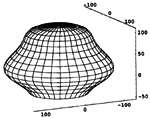	Márta Szilvási-Nagy (szilvasi@math.bme.hu) Zatvaranje cijevi proširenjem B-spline ploha U radu je prikazan algoritam za zatvaranje cijevi reprezentiranih tenzorskim produktom B-spline ploha. Plohe u obliku cijevi proširuju se i zatvaraju pravokutnim dijelovima (trostranim). Geometrijski podaci dijela koji zatvara su zajednički singularni vrh novih rubnih dijelova i rubni uvjeti prvog reda na tom vrhu. Tada se točke proširenja kontrolne mreže računaju iz tih podataka. Korisnički unos algoritma je, osim cijevi, singularna točka zatvaranja. Rubni se uvjeti biraju automatski, a da bi se postigao glatki oblik dijela koji zatvara oni se djelomično računaju i iz uvjeta zaglađivanja. äto više, točka zatvaranja također se može izračunati iz uvjeta zaglađivanja što vodi do automatskog zatvaranja cijevi. Ključne riječi: CAGD, B-spline plohe, zaglađivanje Članak u PDF-u.

	Attila Bölcskei, Emil Molnár (geometry@oliva.eik.bme.hu) Kako projektirati lijepo popločavanje? Motivirani lijepim popločavanjem klasificiramo sva G-popločavanja (T,G) u ravninama konstantne zakrivljenosti s pet baricentričkih trokutastih orbita pod nekontinuiranom grupom izometrija G. U tabeli prikazujemo 13 beskonačnih serija dobivenih popločenja pomoću tzv. D-dijagrama i dodatnih parametara rotacije. Ovisno o parametrima popločenja se mogu realizirati u sfernoj (S²) euklidskoj (E²) ili hiperboličkoj (H²) ravnini. Početni primjeri prikazani su na slikama. Dva zaključna teorema izrečena su u odjeljku 3. Ključne riječi: D-simbol, popločavanje ravnine Članak u PDF-u.

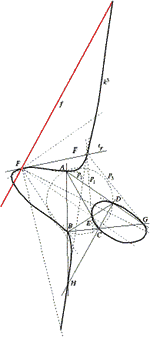	Ana Sliepčević (anasli@juraj.gradnz.grad.hr) Krivulje žarišta u pramenovima krivulja drugog reda i drugog razreda u izotropnoj ravnini Iako su pramen i niz konika u izotropnoj ravnini dualne tvorevine, njihove žarišne krivulje nisu dualne. U članku se dokazuje da je žarišna krivulja rednog pramena konika izotropne ravnine općenito neracionalna kubika. Ova se kubika konstruira u općem i u nekim degeneriranim slučajevima. U pramenu krivulja drugog razreda žarišna je krivulja racionalna kubika s dvostrukom točkom u apsolutnoj točki ravnine. Ova se kubika konstruira u općem i nekim zanimljivim posebnim slučajevima. Ključne riječi: izotropna ravnina, niz konika, pramen konika, žarišna krivulja Članak u PDF-u.

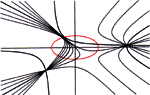	Miljenko Lapaine, Miroslava Lapaine (mlapaine@public.srce.hr) Krivulja središta pramena konika U radu se definira središte konike i krivulja središta pramena konika. Daje se klasifikacija pramena konika s obzirom na eliptičke, paraboličke i hiperboličke krivulje u pramenu. Izvodi se jednadžba krivulje središta pramena konika i ilustrira većim brojem primjera. Ključne riječi: središte konike, pramen konika, krivulja središta pramena konika Članak u PDF-u.