Znanstveno-stručni časopis  
Hrvatskog društva za geometriju i grafiku  

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics


 
Zdravka Božikov (bozikov@cigla.gradst.hr) 

On Symmetric Designs with Parameters (101, 25, 6) 

There is known only one symmetric design with parameters (101, 25, 6) which has a Singer group (see [3]). Consequently, it is of interest to try to construct such a design without a Singer group.  

Key words: symmetric design, automorphism, Frobenius group, orbit structure 

Article in PDF.
 
 Márta Szilvási-Nagy (szilvasi@math.bme.hu) 

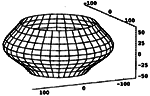
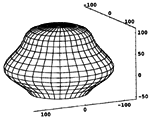
Closing Pipes by Extension of B-Spline Surfaces 

This paper presents an algorithm to close pipes represented as tensor product B-spline surfaces. The tube shaped surface will be extended and closed by degenerate rectangular (three-sided) patches. The geometric data of the closing part are the common singular vertex of the new bordering patches and first order boundary conditions at this vertex. Then the points of the extension of the control net are computed from these data. The user input of the algorithm, besides the pipe, is the single closing point. The boundary conditions are chosen automatically and, in order to achieve a fair shape of the closing part, are partly computed from a fairness condition. Moreover, also the closing point can be computed from the fairness condition, which leads to the automatic closing of the pipe. 

Key words: CAGD, B--spline surface, fairing 

Article in PDF.
Attila Bölcskei, Emil Molnár (geometry@oliva.eik.bme.hu) 

How to Design Nice Tilings? 

Motivated by famous nice tilings we classify all G-tilings (T,G) in the planes of constant curvature with 5 barycentric triangle orbits under a discontinuous isometry group G. We describe the 13 infinite series of the resulting tilings by socalled D-diagrams and additional rotation parameters in our Table. Depending on the parameters, the tilings are realizable in the sphere (S2), in the Euclidean (E2) or Hyperbolic (H2) plane. The starting examples are depicted in our figures. Summarizing two theorems are formulated in Section 3. 

Key words: D-symbol, tiling in the plane 

Article in PDF.
Ana Sliepčević (anasli@juraj.gradnz.grad.hr) 

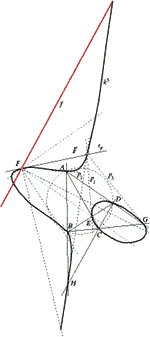
The Focal Curve of the Pencil and the Range of Conics in an Isotropic Plane

Although the pencil and the range of conics in an isotropic plane are dual their focal curves are not dual. In the paper we proved that the focal curve of the pencil of conics in an isotropic plane is in general non rational cubic. This cubic is constructed in the general and for some degenerated cases. For the range of conics the focal curve is the rational cubic with the absolute point of the plane as a double point. This cubic is constructed in general and in some interesting special cases. 

Key words: focal curve, isotropic plane, pencil of conics, range of conics 

Article in PDF.
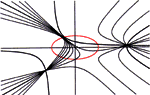Miljenko Lapaine, Miroslava Lapaine (mlapaine@public.srce.hr) 

Curve of Centres of the Conic Section Pencil

The paper defines the centre of conic section and the curve of centres of the conic section pencil. A classification of conic section pencils is given, related to the elliptic, parabolic and hyperbolic type of curves included in the pencil. The equation of the curve of centres of the conic section pencil is derived and illustrated by number of examples. 

Key words: centre of the conic section, conic section pencil, curve of centres of the conic section pencil 

Article in PDF.