Znanstveno-stručni časopis  
Hrvatskog društva za geometriju i grafiku  

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics


 
Maria Kmetóvá and Marta Szilvási-Nagy (kmt@unitra.sk) 

Sphere Covering by Rational Quadratic Beziér Patches 

A covering of the sphere in the three-dimensional Euclidean space is constructed consisting of three-sided and two-sided regions. Each region is represented as a rational quadratic Beziér patch over a triangular or a rectangular domain, respectively. 

Keywords: Beziér patches, rational spline-functions 

Article in PDF.
Daniela Velichová (velichov@dekan.sjf.stuba.sk) 

Geometric Modelling of Hyperpatches 

The paper deals with the modelling of solids (hyperpatches) on the basis of their creative laws. Creative representation of a solid enables to modell also solids with "curve-like" edges, not only solids with the polyhedral boundary as in the boundary representation method. There is provided also the possibility to control a non-homogeneous distribution of the interior points of a solid created as an interpolated figure. Basic notions such as a solid cell, an isoparametric curve segment and an isoparametric surface patch, or tangent space and density vector in a solid point are described and their relevance to the intrinsic geometric properties of the solid is discussed. Composite solid modelling problems on adjoining of the elementar solid cells are mentioned. 

Keywords: solid modelling, creative space, interpolation of hyperpatches 

Article in PDF.
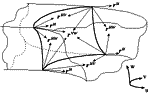
Gloria Bitterfeld (stavrou@swin.edu.au) 

Synthesis of Grassmann Chain Mechanisms in the Plane Using the Ausdehnungslehre and Mathematica 

The Grassmannian mathematical system, well known as the Ausdehnungslehre (Linear Extension Theory) together with the symbolic computation program Mathematica is used to synthesise a class of planer mechanisms, named Grassmann mechanisms. The objective of investigating Grassmann mechanisms is to be able to compute easily the design parameters of the mechanism from given trajectory points. Mechanisms in this class have moving links rotating on pivots and intersecting tracks. The paper reports on the simplest type of synthesis result of Grassmann Chain mechanisms using four given precision points for each mechanism apart to determine the design parameters of the mechanism of the class whose trajectory passes through those points. 

Article in PDF.
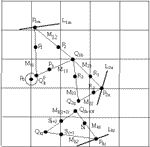
Zvonko Čerin (cerin@cromath.math.hr) 

Triangles from Central Points 

The paper deals with the problem of determining which central points X of the triangle ABC have the property that segments AX, BX, and CX being the sides of a triangle. We shall prove that only thirteen out of hundred and one central points from Kimberling's list have this property. Moreover, the convex hull of ten among these points always consists only of the points having the above mentioned properties. 

Article in PDF.
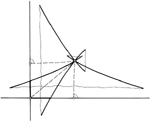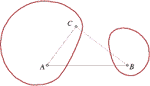
Ivanka Babić, Branko Kučinić (ibabic@juraj.grandz.grad.hr) 

Hyperbolic Perspective I 

In the hyperbolic space the central projection is considered, adjusted to the perspective, by defining the image plane and centre of projection, and the reference plane perpendicular to the image plane. This is the analogy of the so called piercing point method in the Euclidean space supplemented by indefinitely distant elements. The analogue of the method of Monge in H3-space realised on M-model enables necessary constructive procedures. The position and metric relations associated with the reference plane are also worked out thoroughly. Thus, the whole procedure is prepared to be applied.
Basic differences from the perspective of Euclidean space are: h-horizon is hyperbola, there is avoidable hyperbola instead of avoidable line, and the pencils of parallel lines in the plane (1 can be projected into the elliptic, parabolic and hyperbolic pencils (Theorem 3). 

Keywords: hyperbolic space, H-model, central projection, perspective, piercing point method 

Article in PDF.
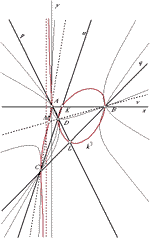Jelena Beban-Brkić (jbeban@geodet.geof.hr) 

On the Focal Curve of Conic Pencils in I2 

Within the classification of conic pencils in the isotropic plane, which has been carried out using methods of analytical geometry and linear algebra, it is specially interesting to observe the curve of isotropic focuses, which is shown to be a 3rd order curve. The properties of this very curve for the discussed, most common subtype of conic pencils, are determined. It is shown that, referring to the selection of the fundamental points, it is possible to determine its shape, and to classify it according to the Newton's principle.
The discussed cases of conic pencils with its focal curves are illustrated with the figures drawn by Mathematica®. 

Key Words: isotropic plane, fundamental points, pencil of conic sections, matrix of quadratic form, eigenvalues, focal curve, Newton's classification 

Article in PDF.
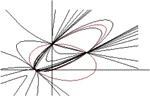Miljenko Lapaine (miljenko.lapaine@public.srce.hr) 

Computer-Aided Graphical Representation of Conic Section Pencils 

In one of the previous works it has been shown how graphic presentation of an individual conics can be programmed on the basis of the coefficient of its equation in the general form. In this paper the conic section pencil is explained, and it is noted that it cannot contain any number of conics of parabolic type, but that only all of them, or two, or one or none can be of such type. The conic section pencil is illustrated through several examples from cartography. 

Keywords: conic, conic section pencils, map projections 

Article in PDF.
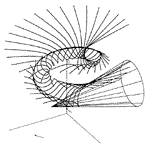Dagmar Szarková (szarkova@dekan.sjf.stuba.sk) 

Computer Aided Calculation of Characteristics Points of Some Envelope Helical Surfaces 

Presented calculations and the choice of variables u,v Î [0,1] of the given basic surface j enable the creation of a versatile programme for the graphical processing of the characteristics not only of the helical but also of the rotational envelope surface F defined by the conical or cylindrical surface. Basic (conical or cylindrical) surface j can be generated from the basic curve defined by the vector function r(u), za u Î [0,1] (1) applying a class of transformations defined by the matrix T(v), for v Î [0,1] (2). The combined analytical and synthetical method resultes in the parametric equations of the characteristics (3) and in the coordinates of the meridian section points. 

Keywords: envelope surface, characteristics, meridian section, creative space, creative representation 

Article in PDF.
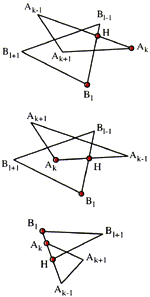Daniela Richtáriková (richtarikova@dekan.sjf.stuba.sk) 

3D Polyhedra Scenes and the Triangulation 

One of the possible utilizations of the planar region triangulation is presented in this paper - a part of the visibility solution in the visualization of the general 3D scene consisting of disjoint polyhedra by the means of computer. 

Keywords: triangulation, potential visibility, polyhedra scene visibility, triangle intersection 

Article in PDF.
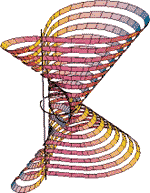Sonja Gorjanc (sgorjanc@grad.hr) 

Generation of Five Types of Ruled Quartics 

According to Sturm ([4], [7]), the ruled quartics are classified into twelve types. In this paper only five types, where directing curves can be conics and straight lines are selected and there is one or more examples given for each of them. In these examples we described the constructive generation of the surfaces, and by means of their parametric equations we made the graphics in Mathematica 3.0. 

Keywords: ruled quartics, ruled surfaces 

Article in PDF.