 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
| Filipe Bellio, Ronaldo Garcia, Dan Reznik (filipe.bellio.nobrega@gmail.com, ragarcia@ufg.br, dreznik@gmail.com)
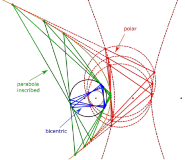
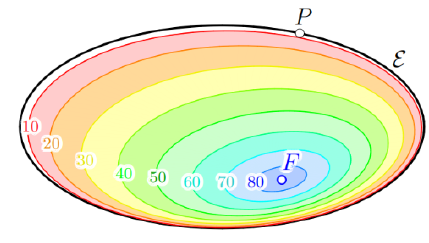
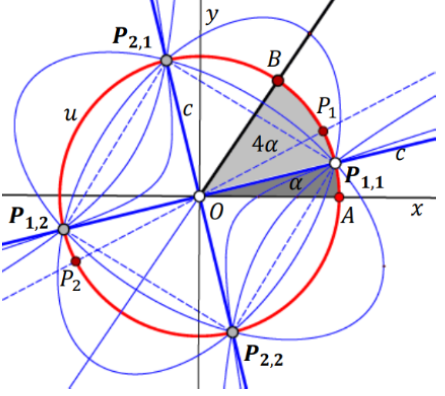
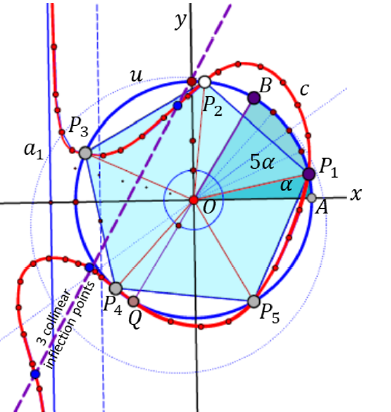
Ponceletovi poligoni upisani paraboli i dobiveni iz biocentričkih familijaProučavamo geometrijska mjesta i svojstva familija Ponceletovih poligona upisanih paraboli koji omataju kružnicu sa središtem u fokusu parabole. Ova familija je polarna slika specijalnog slučaja bicentrične familije s obzirom na svoju opisanu kružnicu. Opisujemo uvjete zatvaranja, geometrijska mjesta, i nove invarijante. |
|
| Ronaldo Garcia, Liliana G. Gheorghe, Peter Moses, Dan Reznik (ragarcia@ufg.br, liliana@dmat.ufpe.br, moparmatic@gmail.com, dreznik@gmail.com)
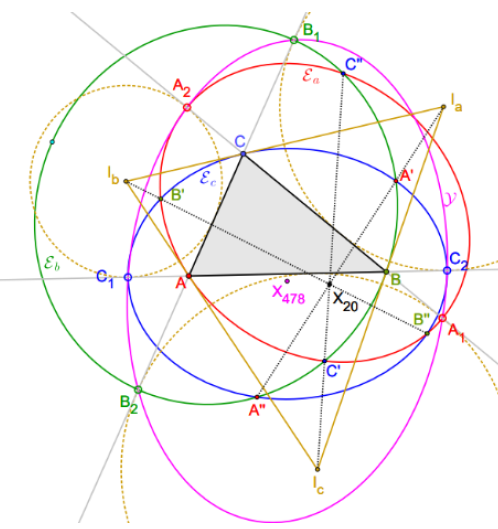
Trijade konika pridruženih trokutuPodsjećamo na konstrukcije temeljene na trijadama konika sa žarištima u parovima vrhova referetnog trokuta. Nalazimo da njihovih 6 vrhova leži na dobro poznatim konikama čiji tip analiziramo. Za ove konike dajemo uvjete da budu kružnice i/ili degenerirane konike. U slučaju degeneriranih konika proučavamo geometrijsko mjesto njihovog središta.Ključne riječi: trokut, konika, Carnot, Soddyjeve kružnice  Article in PDF. Article in PDF. |
|
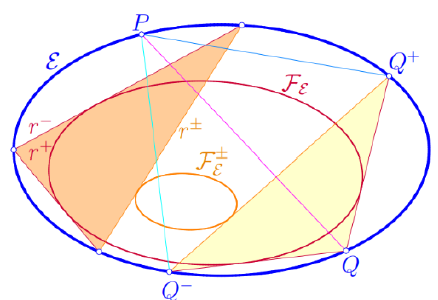
| Boris Odehnal (boris.odehnal@uni-ak.ac.at)
Pramenovi Frégierovih konikaZa svaku točku P na konici c, involucija pravih kutova
u točki P inducira eliptičnu involuciju na konici c čije se
središte F zove Frégierova točka od P. Zamjena pravih kutova u točki P između označenih krakova s proizvoljnim kutom f vodi ka projektivnom preslikavanju u pramenu točke
P, a tako i na konici c. Pravci koji povezuju odgovarajuće
točke na konici c više ne prolaze kroz jednu točku nego
omataju koniku f koja se vidi kao generalizacija Frégierove
točke i zvat će se generalizirana Frégierova konika. Mijenjajući kut, dobivamo pramen generaliziranih Frégierovih
konika koji je pramen treće vrste. Proučavat ćemo tako
definirane konike i otkriti među ostalim i generalizirane
familije Ponceletovih trokuta. |
|
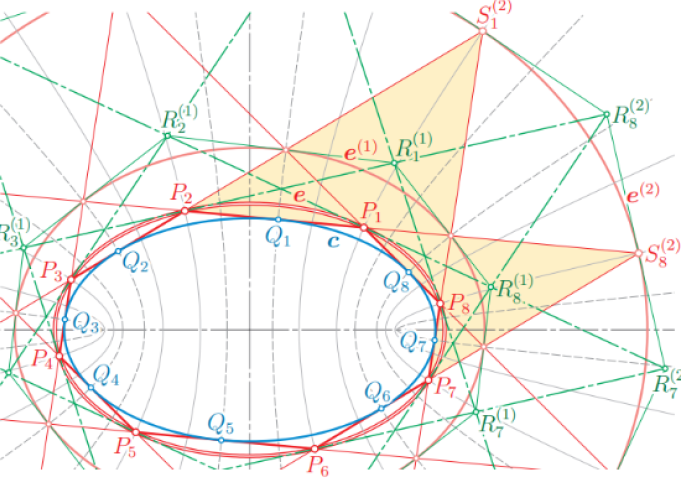
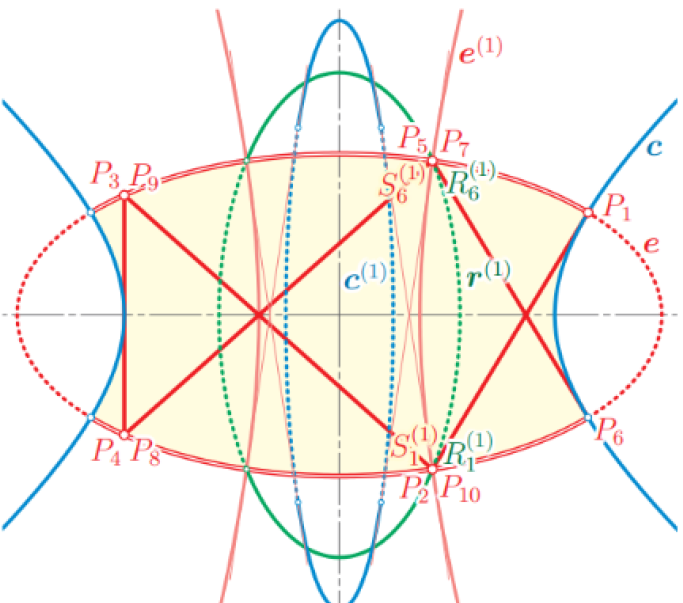
| Helmuth Stachel (stachel@dmg.tuwien.ac.at)
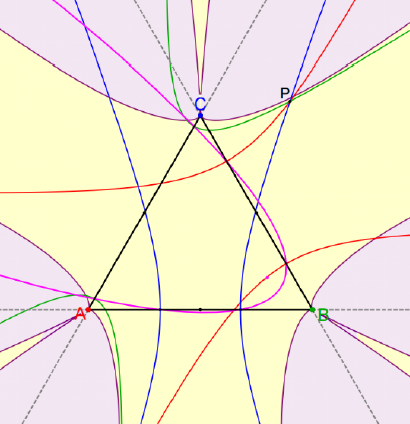
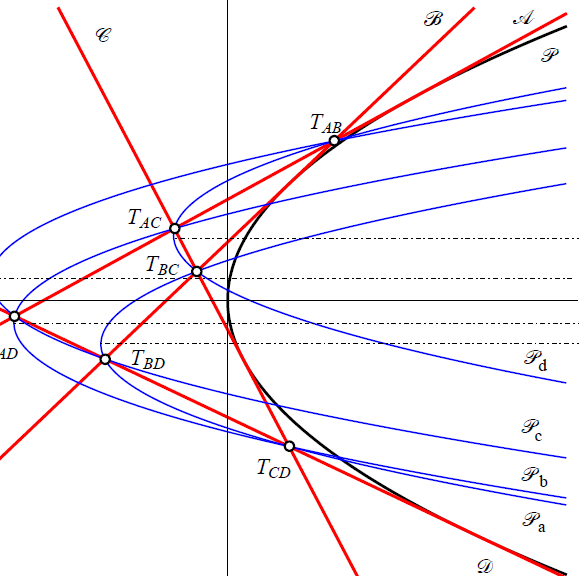
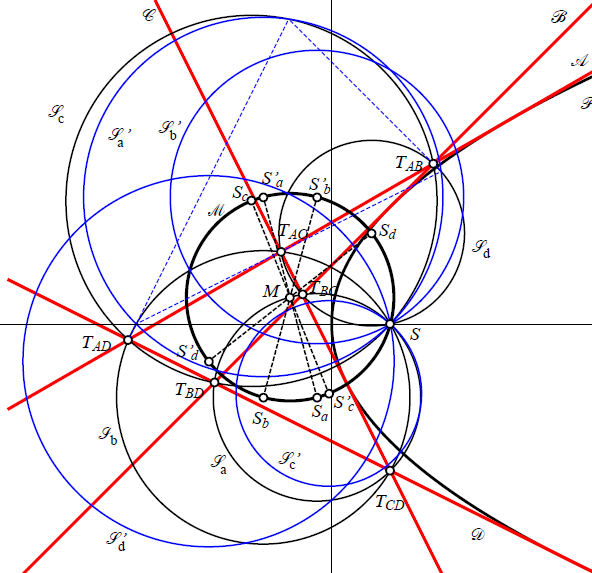
Trojka projektivnih biljaraProjektivni biljar je poligon u realnoj projektivnoj ravnini koji ima upisanu i opisanu koniku. Poput klasičnih biljara u konikama, sjecišta produljenih stranica projektivnog biljara se nalaze na familiji konika koje tvore pridruženu Ponceletovu mrežu. Proširujemo projektivni biljar unutarnjim i vanjskim biljarom i otkrivamo mnoštvo veza između pridruženih mreža i dijagonala, posebice drugih trojki projektivnih biljara. |
|
| Hans Dirnböck, Gunter Weiss (weissgunter@gmx.at)
Ponovno razmatranje trisekcije kuta metodom Jánosa BolyaijaJ. Bolyai je predložio elegantnu metodu za trisekciju kuta određivanjem sjecišta lukova jedinične kružnice s lukovima jednakostranićne hiperbole c. Vrijedno je istražiti geometrijsku pozadinu ovog postupka te ga koristiti kao temeljnu ideju za pronalaženje n-tog dijela zadanog kuta. U ovom radu primijenit ćemo navedenu ideju u trivijalnom slučaju n = 4, te za n = 5. Slijedeći Bolyaija, u slučaju n = 5 jediničnu kružnicu treba presječi kubnom krivuljom c. U tom slučaju, kao i u slučajevima n ≥5, nalazimo samo numerička rješenja, što pokazuje ograničenost Bolyaijeve metode. Stoga predlažemo i drugu konstrukciju, ovaj put utemeljenu na epicikloidi upisanoj jediničnoj kružnici. Ovom metodom moguće je čak konstruirati n/m -ti dio zadanog kuta.
|
|
| Vladimir Volenec, Ema Jurkin, Marija Šimić Horvath (volenec@math.hr, ema.jurkin@rgn.unizg.hr, marija.simic@arhitekt.hr)
Potpuni četverostran u pravokutnim koordinatamaU radu proučavamo potpuni četverostran u euklidskoj ravnini. Poput trokuta i potpuni četverostran ima mnogo zanimljivih svojstava te pridruženih točaka, pravaca i konika. Ovdje je proučavanje provedeno korištenjem pravokutnih koordinata, simetrično po sve četiri stranice četverostrana s četiri parametra a, b, c, d. Proučavamo svojstva točaka, pravaca i kružnica pridruženih četverostranu. Gotovo sve tvrdnje prikazane u ovom radu su dobro poznate, ali su se ipak ponegdje usput pojavili i neki novi rezultati.
|