 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
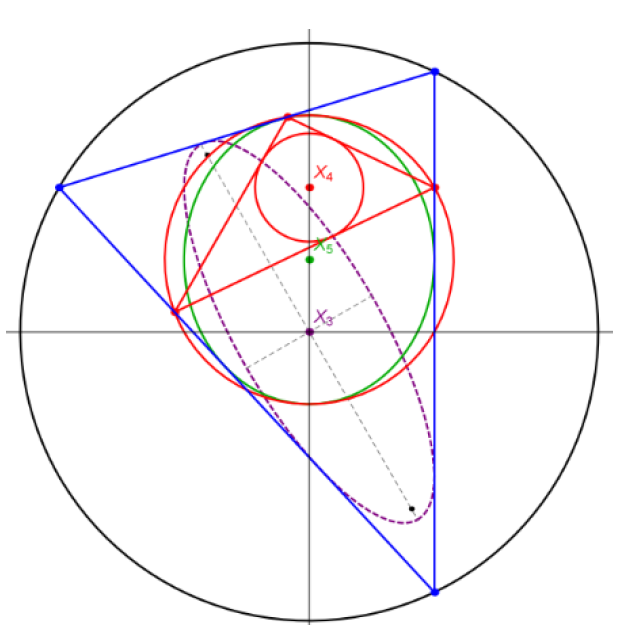 | Ronaldo Garcia, Dan Reznik (ragarcia@ufg.br, dreznik@gmail.com)
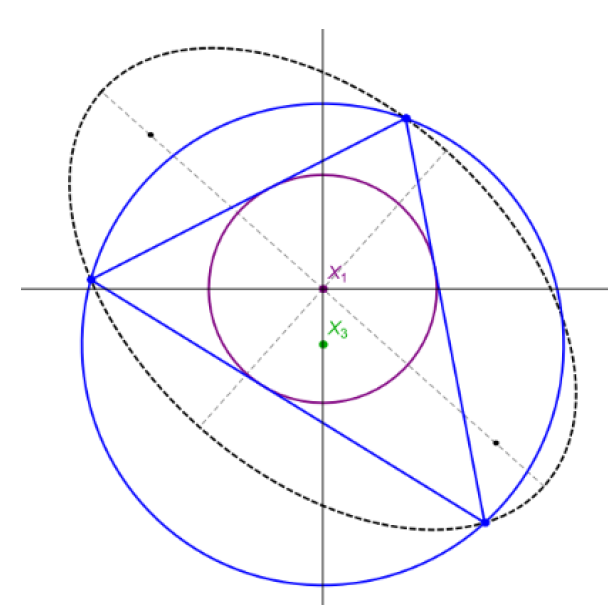
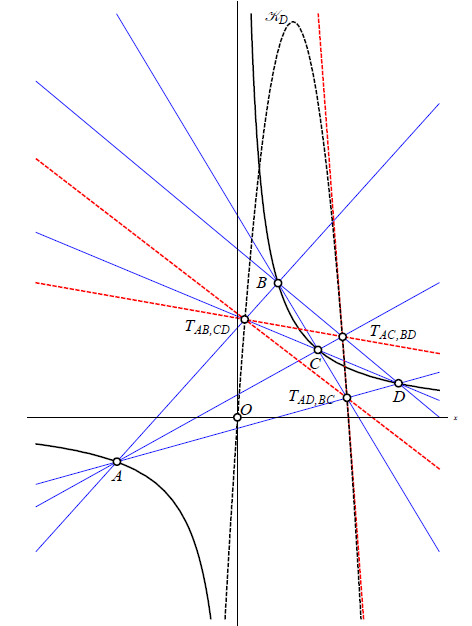
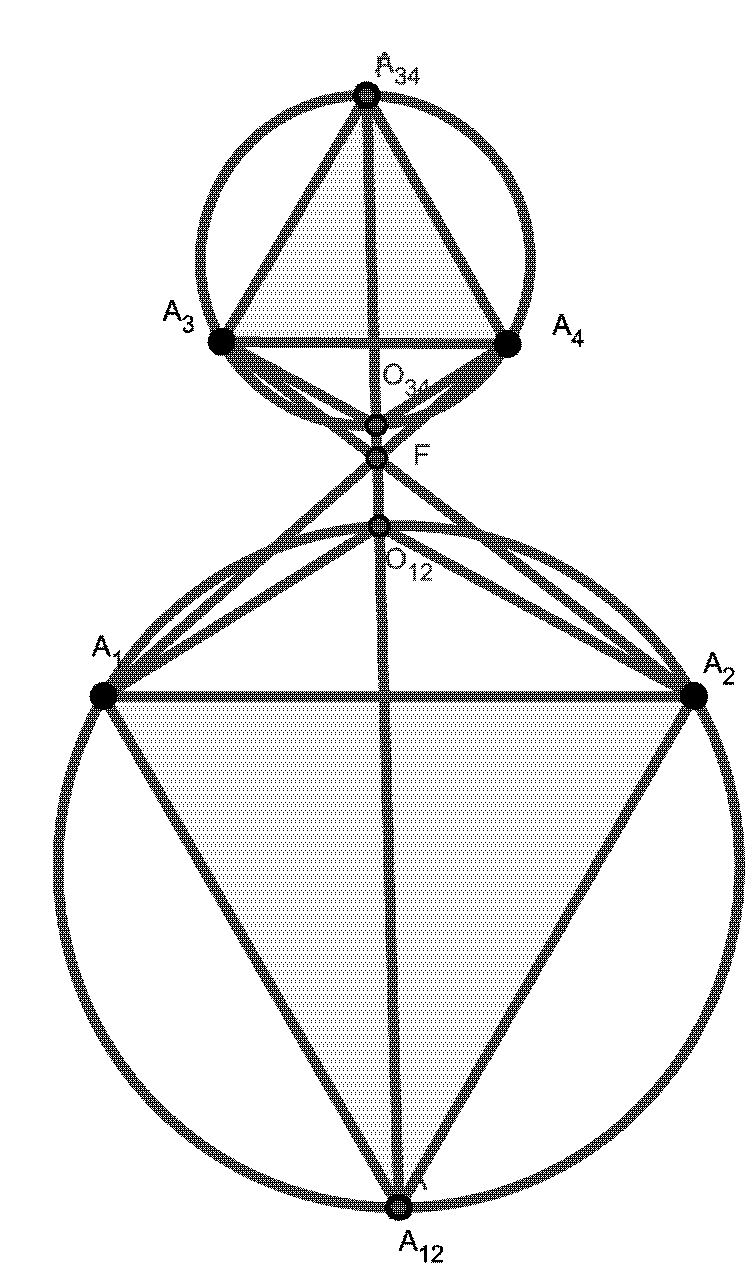
Povezivanje Ponceletovih 3-periodika po njihovim svojstvimaUspoređujemo tipove geometrijskih mjesta točaka i invarijanti u Ponceletovim familijama upisanim u tri različita para koncentričnih elipsi: (i) elipsa - upisana kružnica, (ii) opisana kružnica - upisana elipsa i (iii) homotetične elipse. Njihova metrička svojstva su uglavnom identična svojstvima triju dobro proučavanih familija: eliptični bilijar (par sa zajedničkim fokusima), Chappleovi poristični trokuti i Brocardov porizam. Zbog toga ih organiziramo u tri povezane grupe. |
|
| Hiroshi Okumura (hokmr@yandex.com)
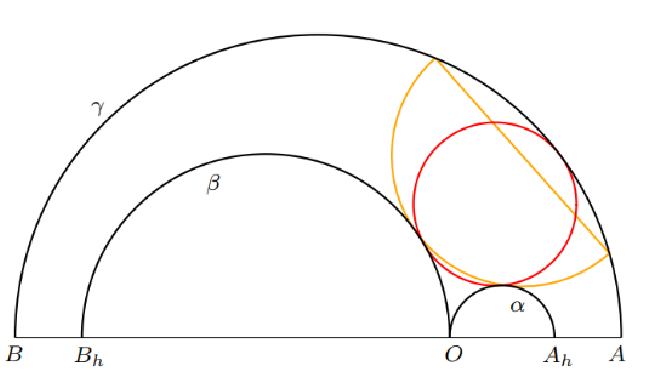
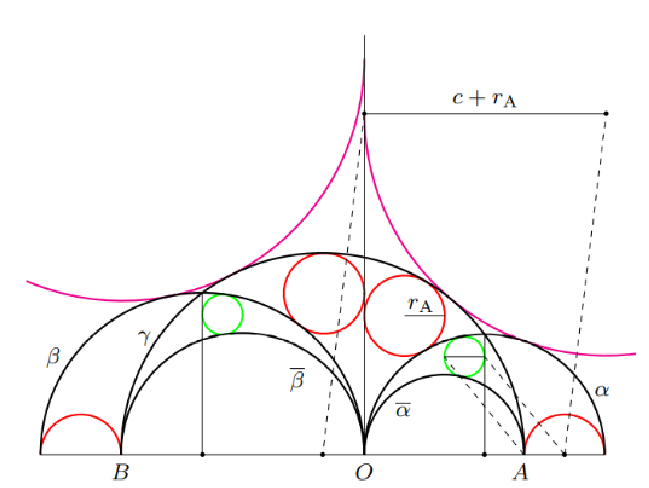
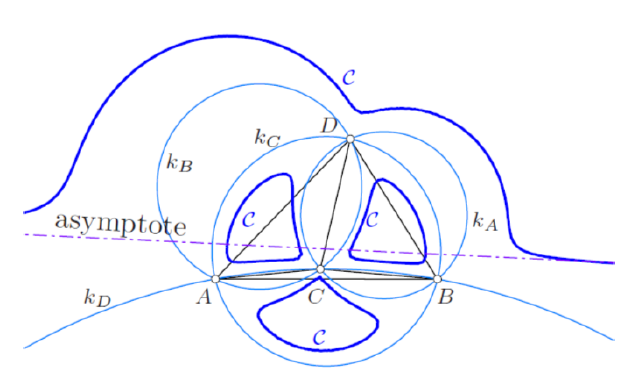
Polukružnice u arbelosima s produžecima i dijeljenje s nulomU radu proučavamo posebne polukružnice, one čije krajnje točke leže na jednoj kružnici, u poopćenim arbelosima s produžecima kao u [4] uz korištenje dijeljenja s nulom.Ključne riječi: arbelosi, arbelosi s produžecima, Aida arbelosi, polukružnice s diranjem u krajnjim točkama, unutarnje polukružnice, Arhimedove polukružnice, dijeljenje s nulom  Article in PDF. Article in PDF. |
|
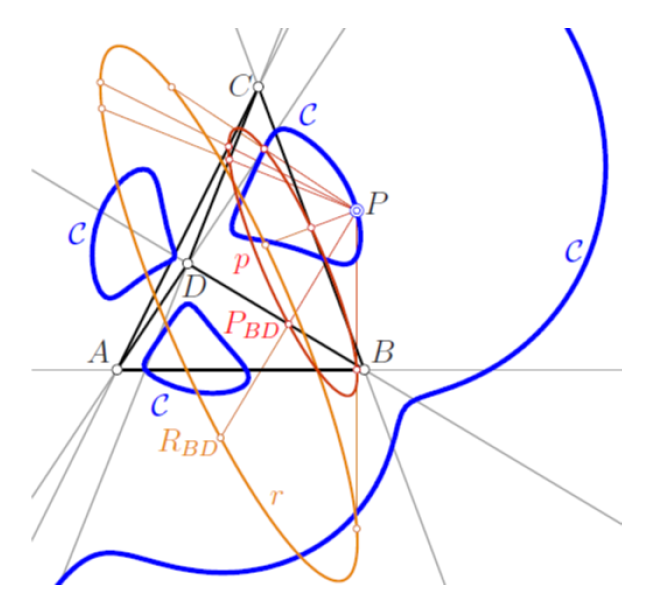 | Boris Odehnal (boris.odehnal@uni-ak.ac.at)
Rijetkost u geometriji: septikaU radu se proučava geometrijsko mjesto C točaka ravnine čija nožišta na
šest strana potpunog četverovrha leže na
jednoj konici. Pokazuje se da je u euklidskoj ravnini C algebarska krivulja 7. reda i roda 5, a ne 12. reda kao
što bi se očekivalo. Septike se u geometriji rijetko pojavljuju pa je ta
činjenica potaknula detaljnije proučavanje
ove krivulje. Promatraju se njezini singulariteti, žarišta
i one točke krivulje C čije su nožišne konike raspadnute.
Zatim se pokazuje da se septika pojavljuje kao geometrijsko mjesto točaka u jednom općenitijem slučaju. Nadalje,
opisuju se oni slučajevi kad se C raspada ili kad je reda
manjeg od 7 u ovisnosti o obliku polaznog četverostrana. |
|
| Marija Šimić Horvath, Vladimir Volenec (msimic@arhitekt.hr, volenec@math.hr)
Dijagonalni trokut netetivnog četvreovrha u izotropnoj ravniniGeometrija netetivnog četverovrha u izotropnoj ravnini uvedena je u člancima [2] i [6]. Ovdje se proučava dijagonalni trokut i daju se neka njegova lijepa svojstva. |
|
| Milena Stavrić, Albert Wiltsche, Gunter Weiss (mstavric@tugraz.at, wiltsche@tugraz.at, weissgunter@gmx.at)
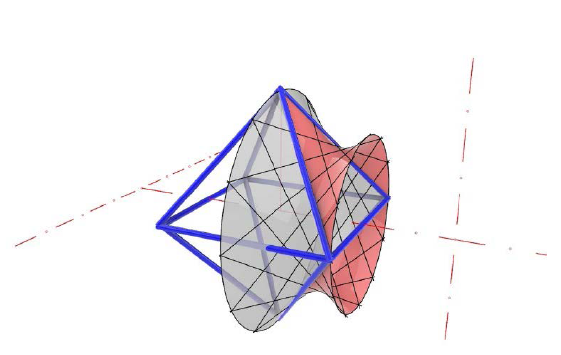
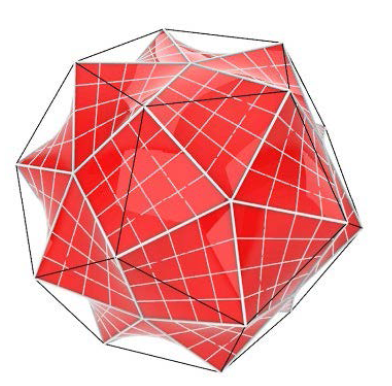
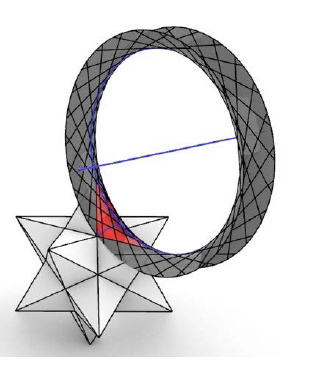
Poliedri čije su strane dijelovi posebnih kvadrikaPreuzimamo ideju Oswalda Gieringa (vidi [1] i [2]), koji je par strana poliedra zamijenio dijelom hiperboličnog paraboloida i povezao bridni četverostran poliedra s pramenom kvadrika određenim tim četverostranom. Očito se samo pravčaste kvadrike mogu pojaviti. Postoji jednostavan nužan uvjet postojanja pravčastog rotacijskog hiperboloida kroz dani četverostran. Posebno, ako (prostorni) četverostran ima jednu ravninu simetrije, onda postoje dva rotacijska hiperboloida kroz njega, a ako je četverostran jednakostraničan, onda pramen kvadrika kroz njega sadrži čak tri rotacijska hiperboloida s međusobno okomitim osima. Na primjer, kod pravilne dvostruke piramide, kao što je oktaedar, osi rotacijskih hiperboloida su, s jedne strane, u ravnini pravilnog mnogokuta (osnovke), a s druge strane, su usporedne s osi simetrije dvostruke piramide. Parove strana (trokute) ne samo Platonovih tijela, već svih poliedara kod kojih se mogu definirati bridni četverostrani, moguće je zamijeniti dijelovima kvadrika, i na taj način proizvesti krovišta od arhitektonskog značaja. Posebno zanimljiva krovišta mogu nastati primjenom dijelova hiperboličnih paraboloida, ili kao što je ovdje prikazano, rotacijskih hiperboloida koje je jednostavno i realizirati u praksi.
|
|
| Anastasios N. Zachos (azachos@gmail.com)
Generalizirana regularnost i simetrija "botanologičnih" mrežaIzvodimo generaliziranu regularnost konveksnih četverokuta u \(\mathbb{R}_2\) koja daje novu evolucijsku klasu konveksnih četverokuta koju mi nazivamo generalizirani regularni četverokuti u \(\mathbb{R}_2\): Svojstvo generalizirane regularnosti kaže da Simpsonov pravac definiran s dvije Steinerove točke prolazi odgovarajućom Fermat-Torricellijevom točkom tog istog četverokuta. Dokazujemo da se klasa generaliziranih regularnih konveksnih četverokuta sastoji od konveksnih četverokuta takvih da su njihove dvije nasuprotne stranice paralelne. Rješavamo problem vertikalne evolucije "botanologičnog palca" (težinska mreža, u oba smjera) s obzirom na granični pravokutnik u \(\mathbb{R}_2\) koji ima dva korijena, dvije grane, bez da ima glavnu granu, primjenjujući svojstvo generalizirane regularnosti težinskih pravokutnika. Pokazujemo da dvije grane imaju jednake težine kao i dva korijena ako "palac" nasljeđuje simetriju s obzirom na poluokomit pravac dvaju nasuprotnih stranica pravokutnika koji je okomit na tlo (jednake grane i jednaki korijeni). Geometrijski, rotacijski i dinamični plasticitet težinskih mreža za granični generalizirani regularni tetraedar i težinski regularni tetraedar vodi ka stvaranju "botanologičnih palčeva" i "botanologičnih" mreža (s glavnom granom) koja ima simetrične grane.
|
|
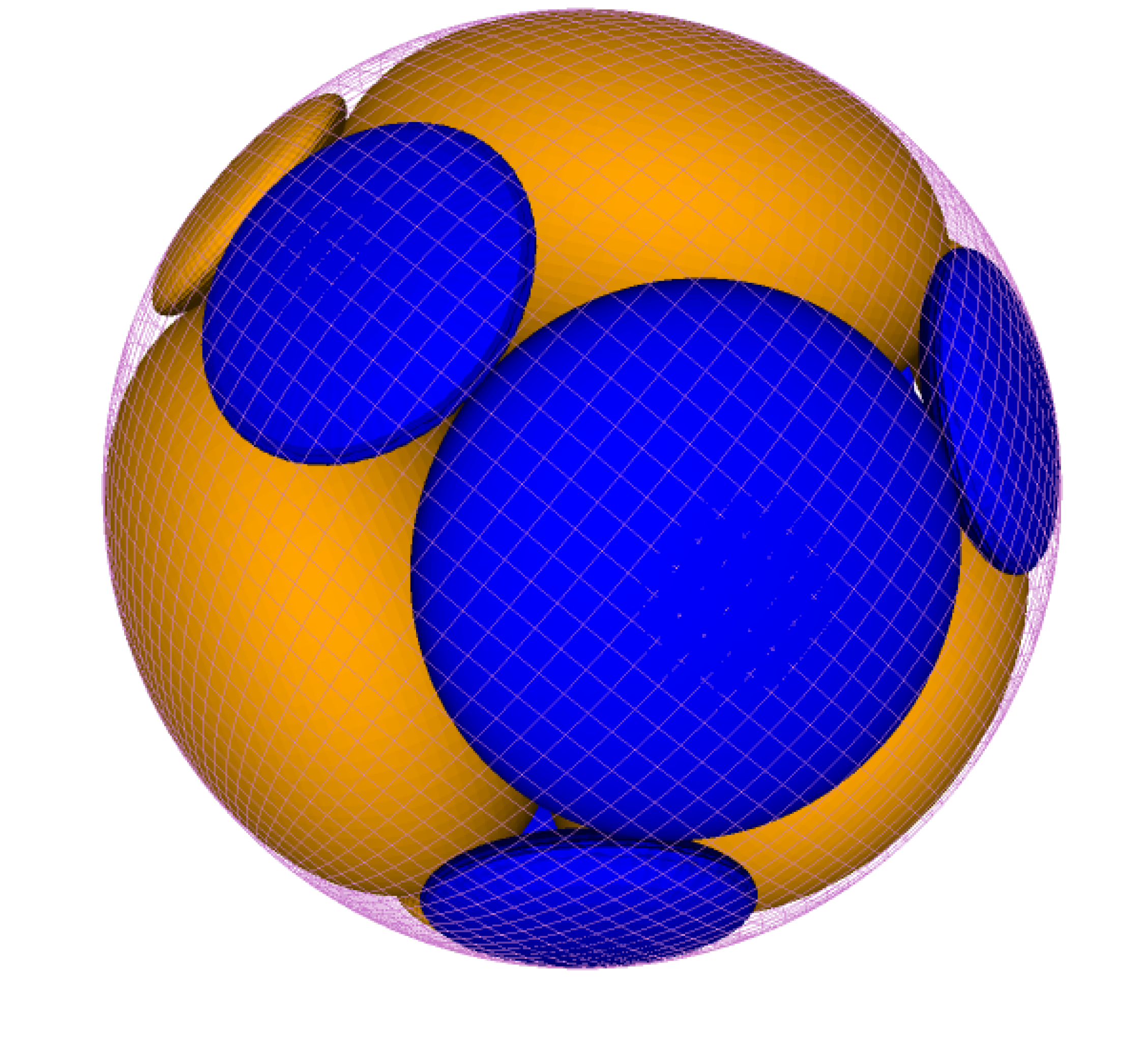
| Arnasli Yahya, Jenö Szirmai (arnasli@math.bme.hu, szirmai@math.bme.hu)
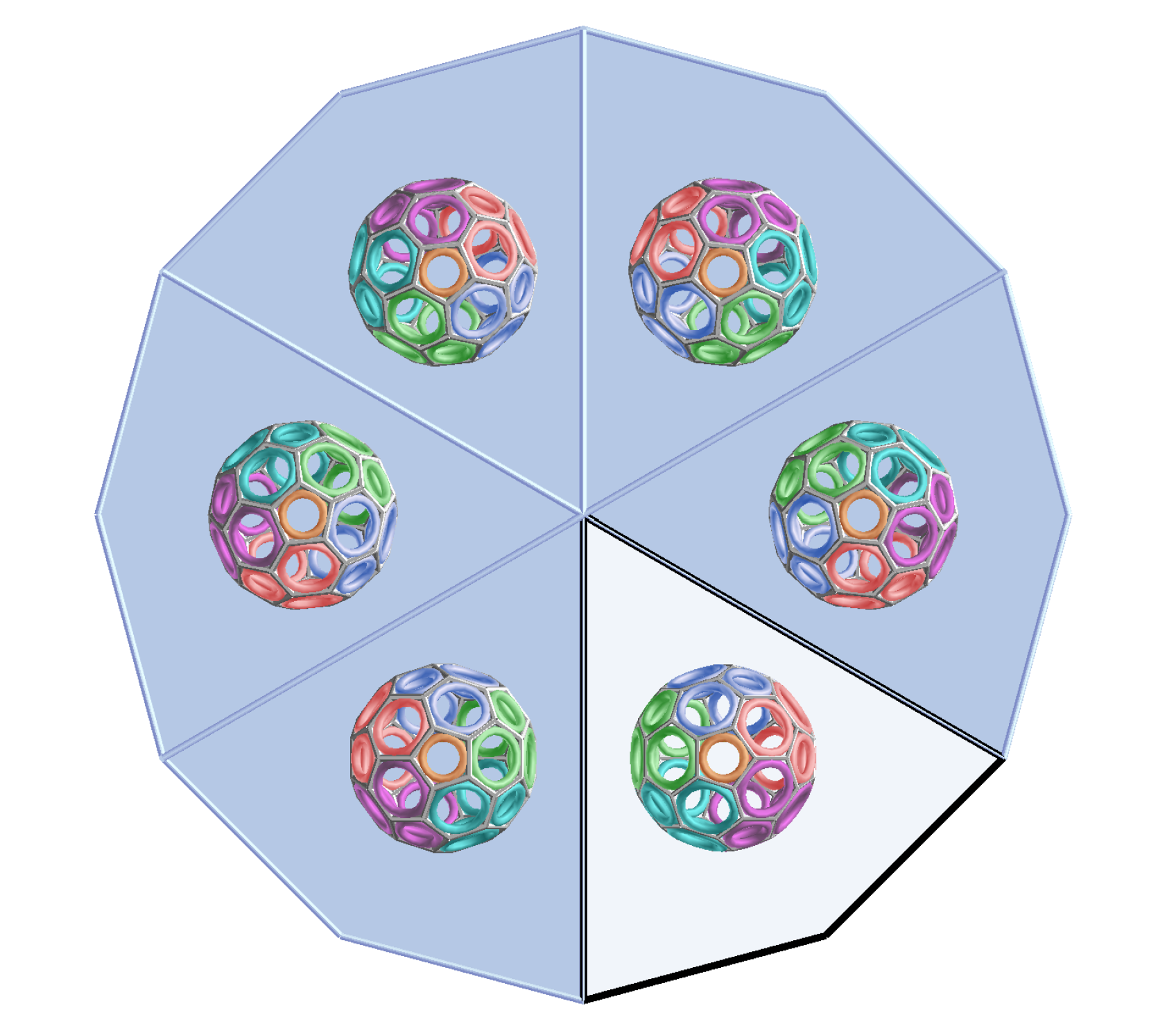
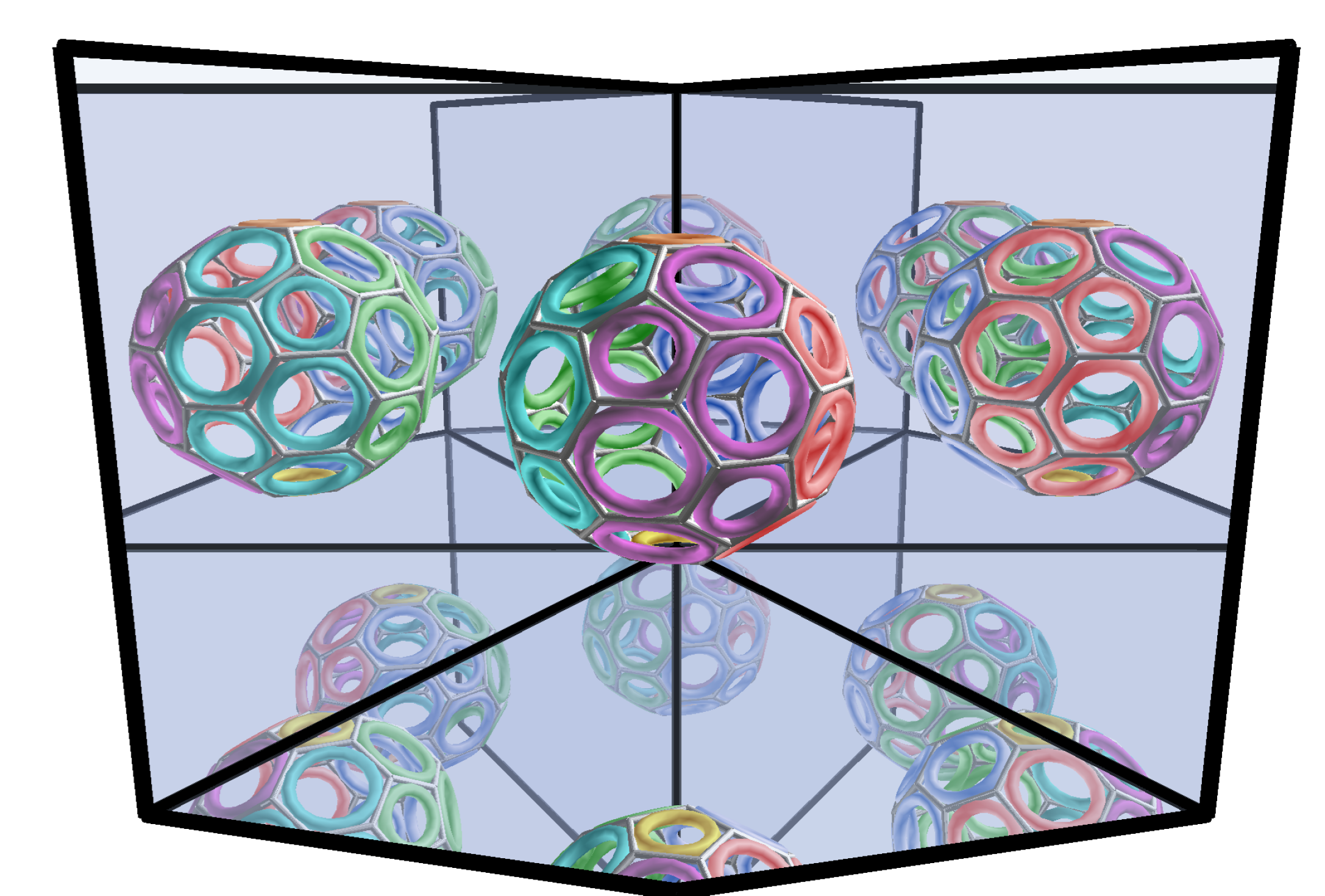
Vizualizacija pakiranja sfera i horosfera povezanih s Coxeterovim popločavanjem krnjim ortoshemama paralelnih stranaU ovom radu opisujemo i vizualiziramo najgušće konfiguracije pakiranja sfera i horosfera na krnjim 3- dimenzionalnim hiperboličnim Coxeterovim ortoshemama s paralelnim stranama, koristeći rezultate [24]. Ovi lijepi rasporedi pakiranja opisuju i pokazuju vrlo zanimljivu strukturu spomenutih ortoshema i odgovarajuće Coxeterove zrcalne grupe. Koristimo sferni Beltrami-Cayley-Kleinov model 3-dimenzionalnog hiperboličnog prostora \(\mathbb{H}^3\). Slike su izrad-ene programskim jezikom Python.
|
|
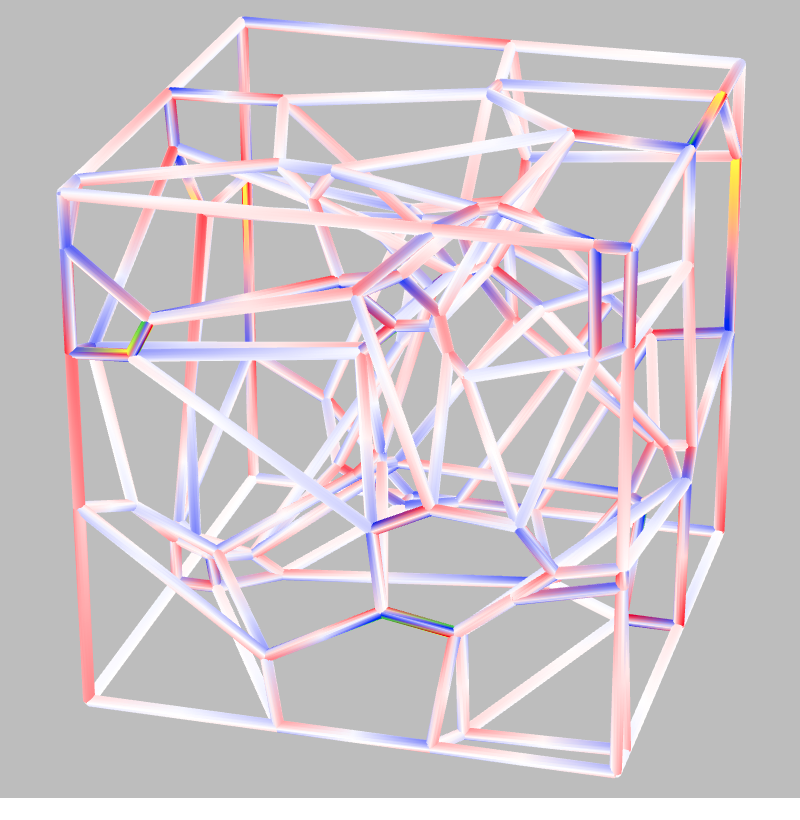
| Leonard Weydemann, Christian Clemenz, Clemens Preisinger (leonard.weydemann@uni-ak.ac.at, christian.clemenz@uni-ak.ac.at, clemens.preisinger@uni-ak.ac.at)
O strukturalnim svojstvima Voronoi dijagramaVoronoi dijagram je tehnika popločavanja koja čini particiju prostora s obzirom na udaljenosti od zadanog skupa objekata koje nazivamo lokacije (en. seeds). Uzorke koji nastaju tokom bioloških procesa (na primjer u staničnom tkivu) možemo modelirati biomimikrijskim procesima korištenjem Voronoi dijagrama. Kako je izvor takvih struktura prirodan, proučavamo fizička svojstva takvih uzoraka da bismo ispitali njihovu optimalnost s obzirom na ograničenja koja nameću vanjska geometrija i prirodne sile. U ovom članku opisujemo slučajeve u kojima je Voronoi popločavanje (strukturalno) optimalno proučavanjem nedavnih ispitivanja koja ovo popločavanje koriste u različitim razmjerima. Da bismo usporedili svojstva slučajnog te optimiziranog Voronoi popločavanja i metode pravilnog popločavanja, razvili smo simulaciju korištenjem Karamba3D, alata za parametarsko strukturalno inženjersko modeliranje unutar programa Rhinoceros3D. Novost ovog istraživanja je predstavljanje jednostavne i izravne simulacije Voronoi dijagrama, isticanje njenih prednosti nad pravilnim popločavanjima te pregled korištenja tih prednosti u naprednijim pristupima iz literature.
|
|
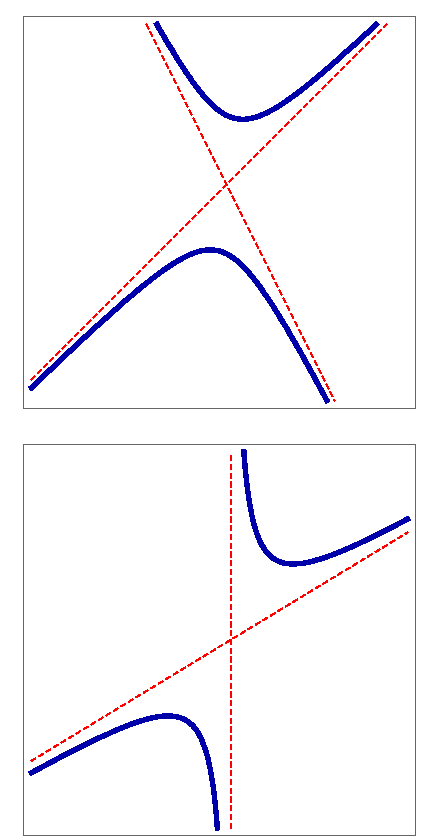
| Ana Katalenić, Aleksandra Čižmešija, Željka Milin Šipuš (akatalenic@foozos.hr, cizmesij@math.hr, zeljka.milin-sipus@math.hr)
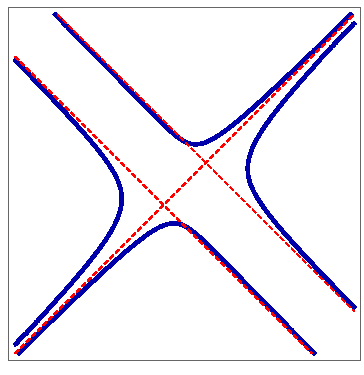
Asimptote ravninske krivulje - ponovni pogledU ovom radu dajemo pregled osnovnih ideja i rezultata vezanih uz asimptote ravninskih krivulja. Raspravljamo o njihovim različitim definicijama, naime, o definiciji kao o graničnom položaju tangenata, o definiciji kao o tangenti u beskonačnosti, te konačno o definiciji koja zahtijeva da udaljenost između točke krivulje i asimptote teži 0 kako se točka kreće duž beskonačne grane krivulje. Također se prisjećamo metode određivanja asimptota algebarskih krivulja iz vodećih koeficijenata u njihovoj jednadžbi te navodimo primjere.
|
|
| Christian Clemenz, Leonard Weydemann (christian.clemenz@uni-ak.ac.at, leonard.weydemann@uni-ak.ac.at)
Tehnike zrcaljenja u Real-Time računalnoj graficiZrcaljenja imaju dugu povijest primjene u računalnoj grafici zbog njihove važnosti u prenošenju realističnosti prikaza te prikaza dubine i omjera na slikama. Pri implementaciji zrcaljenja dolazimo do raznih teškoća i svako novo rješenje često imaju svoju cijenu. Pristupi implementacije ovise o geometriji plohe na kojoj leži prikaz, što je ploha zakrivljenija, to je teže postići vjerni prikaz. Tehnike možemo kategorizirati u one koje rade sa stvarnom geometrijom zrcaljenih objekata te one koje rade samo sa slikama objekata. Kod zakrivljenih ploha koriste se tehnike bazirane na slikama, dok se kod ravninskih ploha koristi zrcaljena geometrija jer nema iskrivljenja. Zahvaljujući trenutnom razvoju tehnologije grafičkih hardvera, metoda praćenja zraka (ray tracing) postaje sve isplativija u real-time primjeni. Mnoga moderna rješenja kombiniraju razne pristupe i dolazi do hibridnih tehnika. U ovom radu dajemo pregled tehnika korištenih u primjeni računalne grafike za postizanje real-time zrcalnih slika. Naglašavamo probleme koji nastaju pri korištenju određene tehnike te njihove mogućnosti u pogledu stvaranja međuzrcaljenja. Naposljetku, opisujemo kako moderni alati za renderiranje rješavaju probleme zrcaljenja.
|