 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
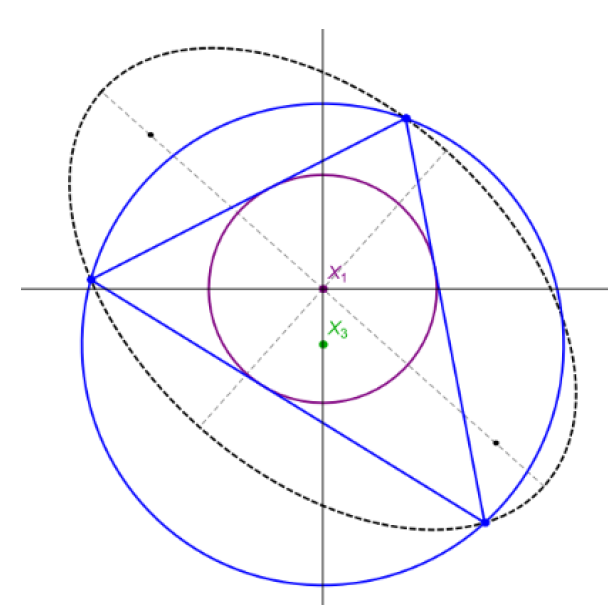
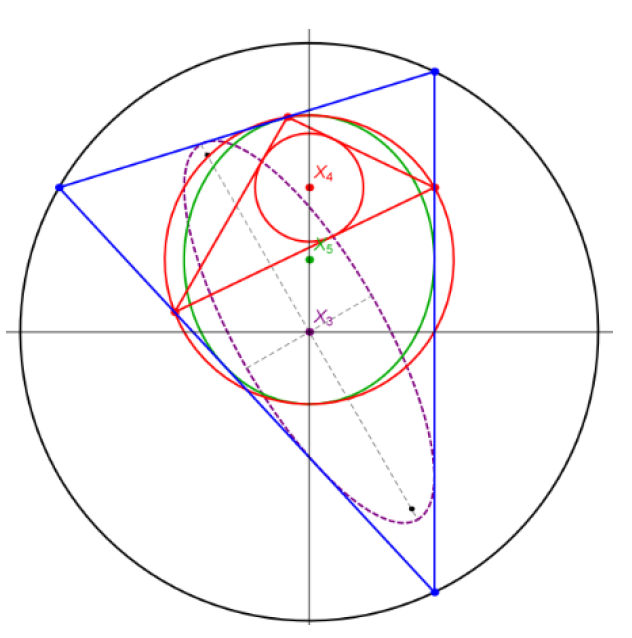
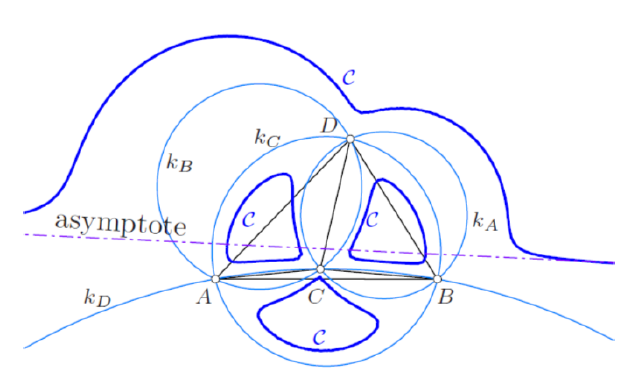
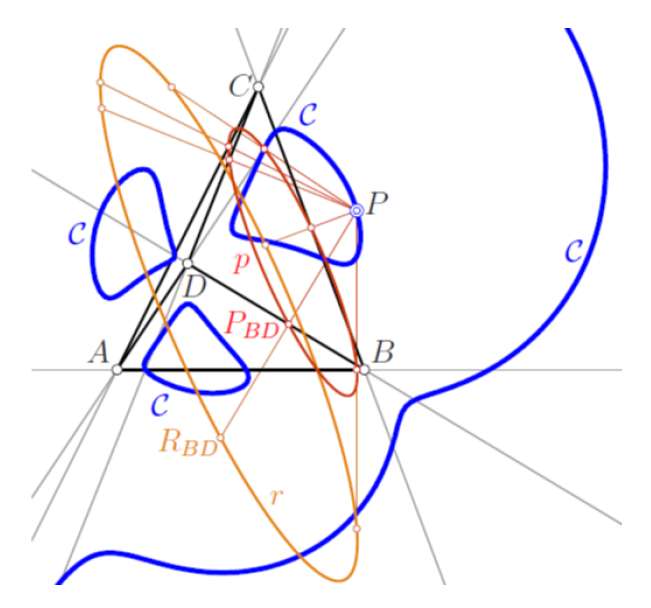
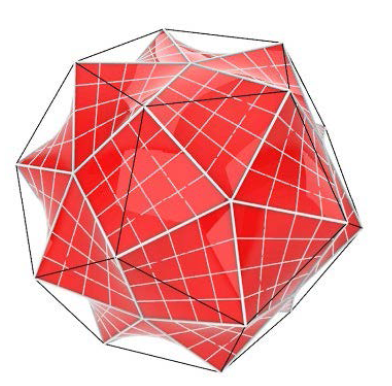
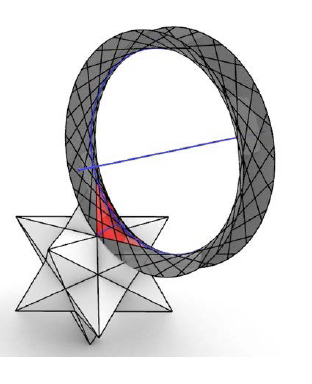
| Ronaldo Garcia, Dan Reznik(ragarcia@ufg.br, dreznik@gmail.com)Family Ties: Relating Poncelet 3-Periodics by their PropertiesWe compare loci types and invariants across Poncelet families interscribed in three distinct concentric Ellipse pairs:
(i) ellipse-incircle, (ii) circumcircle-inellipse, and (iii) homothetic. Their metric properties are mostly identical to
those of 3 well-studied families: elliptic billiard (confocal
pair), Chapple's poristic triangles, and the Brocard porism.
We therefore organized them in three related groups.
 Article in PDF. Article in PDF. |
|
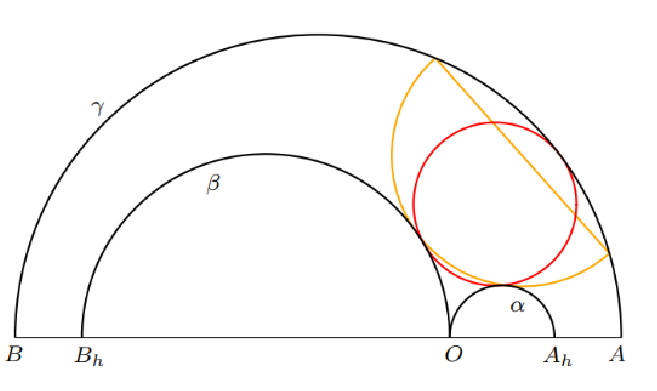
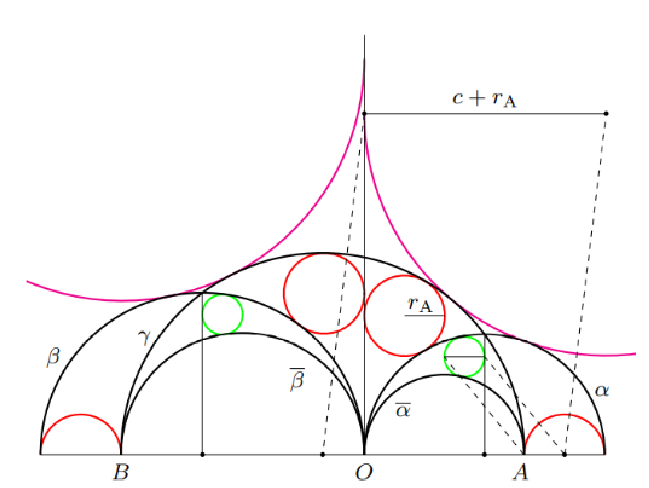
| Hiroshi Okumura (hokmr@yandex.com)
Semicircles in the Arbelos with Overhang and Division by ZeroWe consider special semicircles, whose endpoints lie on
a circle, for a generalized arbelos called the arbelos with
overhang considered in [4] with division by zero. |
| Boris Odehnal (boris.odehnal@uni-ak.ac.at)
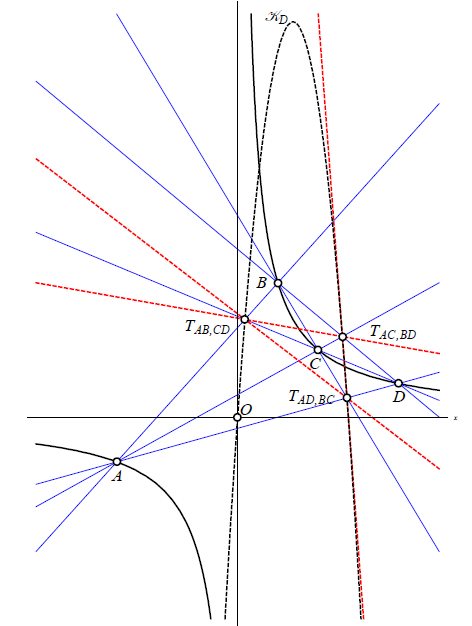
A Rarity in Geometry: a Septic CurveWe study the locus C of all points in the plane whose pedal points on the six sides of a complete quadrangle lie on a conic. In the Euclidean plane, it turns out that C is an algebraic curve of degree 7 and genus 5 and not of degree 12 as it could be expected. Septic curves occur rather seldom in geometry which motivates a detailed study of this particular curve. We look at its singularities, focal points, and those points on C whose pedal conics degenerate. Then, we show that the septic curve occurs as the locus curve for a more general question. Further, we describe those cases where C degenerates or is of degree less than 7 depending on the shape of the initial quadrilateral. Key words: quadrilateral, complete quadrangle, pedal
point, conic, six conconic points, septic curve, Simson line,
Miquel point |
|
| Marija Šimić Horvath, Vladimir Volenec (msimic@arhitekt.hr, volenec@math.hr)
On Diagonal Triangle of Non Cyclic Quadrangle in Isotropic PlaneGeometry of the non cyclic quadrangle in the isotropic
plane was introduced in [2] and [6]. Herein, its diagonal
triangle is studied and some nice properties of it are given. |
|
| Milena Stavrić, Albert Wiltsche, Gunter Weiss (mstavric@tugraz.at, wiltsche@tugraz.at, weissgunter@gmx.at)
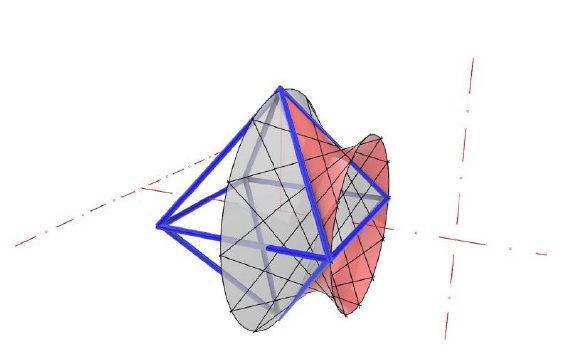
Polyhedrons the Faces of which are Special Quadric PatchesWe seize an idea of Oswald Giering (see [1] and [2]), who
replaced pairs of faces of a polyhedron by patches of hyperbolic paraboloids and link up edge-quadrilaterals of a
polyhedron with the pencil of quadrics determined by that
quadrilateral. Obviously only ruled quadrics can occur.
There is a simple criterion for the existence of a ruled hyperboloid of revolution through an arbitrarily given quadrilateral. Especially, if a (not planar) quadrilateral allows
one symmetry, there exist two such hyperboloids of revolution through it, and if the quadrilateral happens to be
equilateral, the pencil of quadrics through it contains even
three hyperboloids of revolution with pairwise orthogonal axes. To mention an
example, for right double pyramids, as for example the octahedron, the
axes of the hyperboloids of revolution are, on one hand, located in the plane
of the regular guiding polygon, and on the other, they are
parallel to the symmetry axis of the double pyramid. Key words:
polyhedron, quadric, hyperboloid of revolution, Bézier patch |
|
| Anastasios N. Zachos (azachos@gmail.com)
Generalized Regularity and the Symmetry of Branches of "Botanological" NetworksWe derive the generalized regularity of convex quadrilaterals in \(\mathbb{R}_2\) which gives a new evolutionary class of convex quadrilaterals that we call generalized regular quadrilaterals in \(\mathbb{R}_2\) : The property of generalized regularity states that the Simpson line defined by the two Steiner points passes through the corresponding Fermat-Torricelli point of the same convex quadrilateral. We prove that a class of generalized regular convex quadrilaterals consists of convex quadrilaterals, such that their two opposite sides are parallel. We solve the problem of vertical evolution of a "botanological" thumb (a two way communication weighted network) w.r to a boundary rectangle in \(\mathbb{R}_2\) having two roots, two branches and without having a main branch, by applying the property of generalized regularity of weighted rectangles. We show that the two branches have equal weights and the two roots have equal weights, if the thumb inherits a symmetry w.r to the midperpendicular line of the two opposite sides of the rectangle, which is perpendicular to the ground (equal branches and equal roots). The geometric, rotational and dynamic plasticity of weighted networks for boundary generalized regular tetrahedra and weighted regular tetrahedra lead to the creation of "botanological" thumbs and "botanological" networks (with a main branch) having symmetrical branches. Key words:
Fermat-Torricelli problem, Fermat-Torricelli
point, Steiner tree, Steiner points, generalized regular
quadrilaterals, generalized regularity, "thumb" |
|
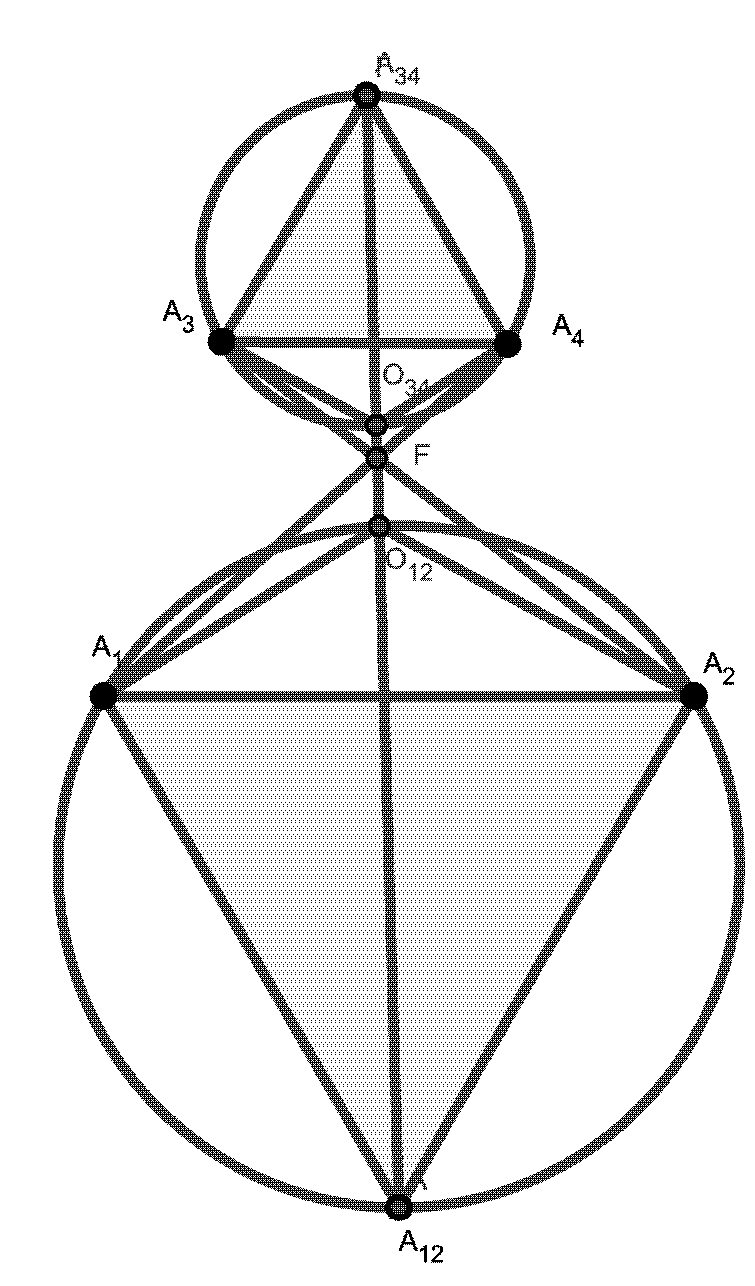
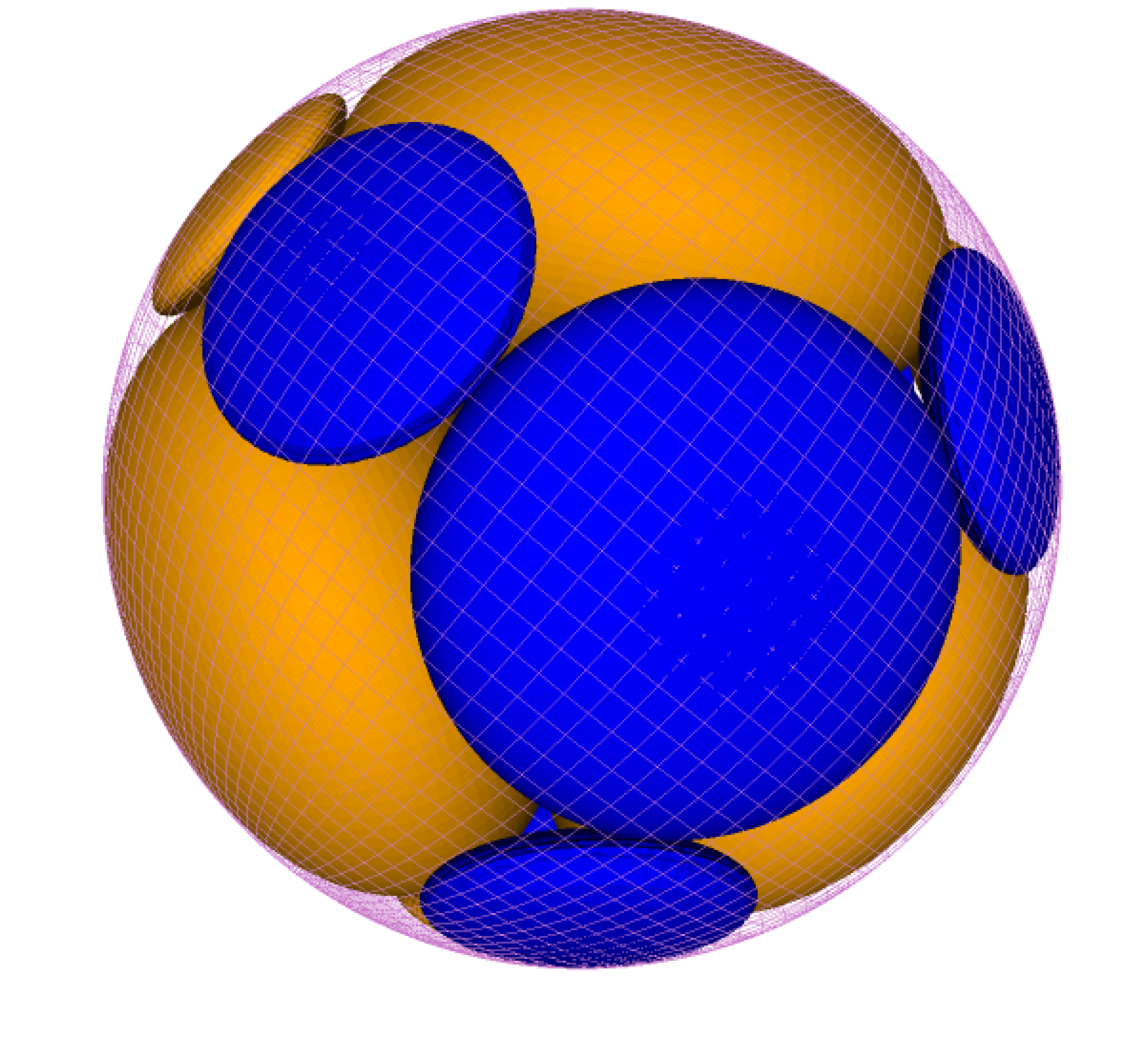
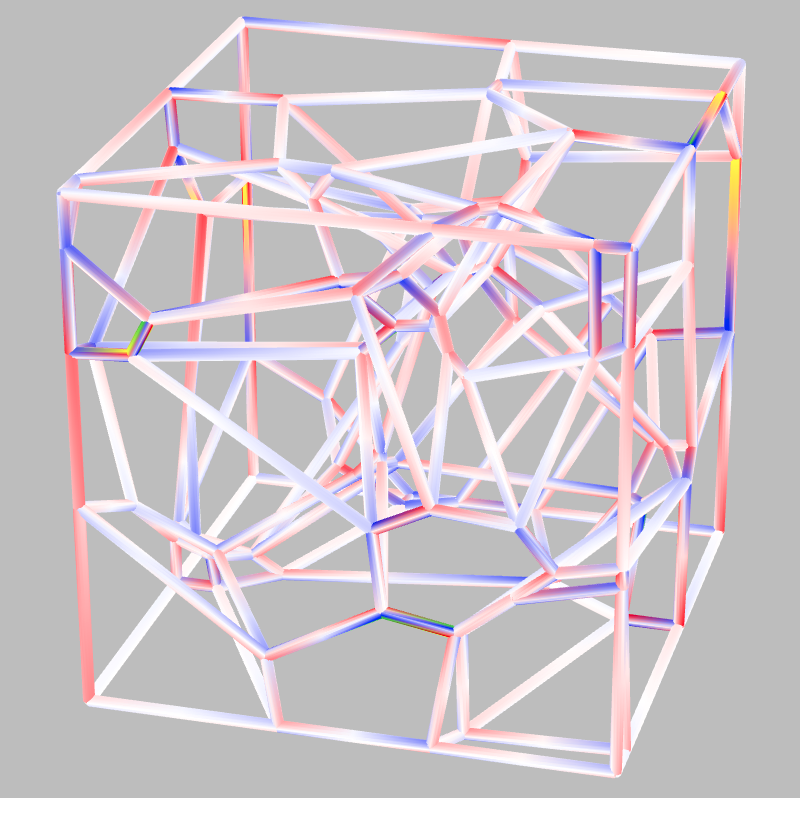
| Arnasli Yahya, Jenö Szirmai (arnasli@math.bme.hu, szirmai@math.bme.hu)
Visualization of Sphere and Horosphere Packings Related to Coxeter Tilings by Simply Truncated Orthoschemes with Parallel FacesIn this paper we describe and visualize the densest ball and horoball packing configurations to the simply truncated 3-dimensional hyperbolic Coxeter orthoschemes with parallel faces, using the results of [24]. These beautiful packing arrangements describe and show the very interesting structure of the mentioned orthoschemes and the corresponding Coxeter reflection group. We use the Beltrami-Cayley-Klein ball model of 3-dimensional hyperbolic space \(\mathbb{H}^3\) , the images were made by the Python programming language. Key words:
Coxeter group, horosphere, hyperbolic geometry, packing, tilings |
|
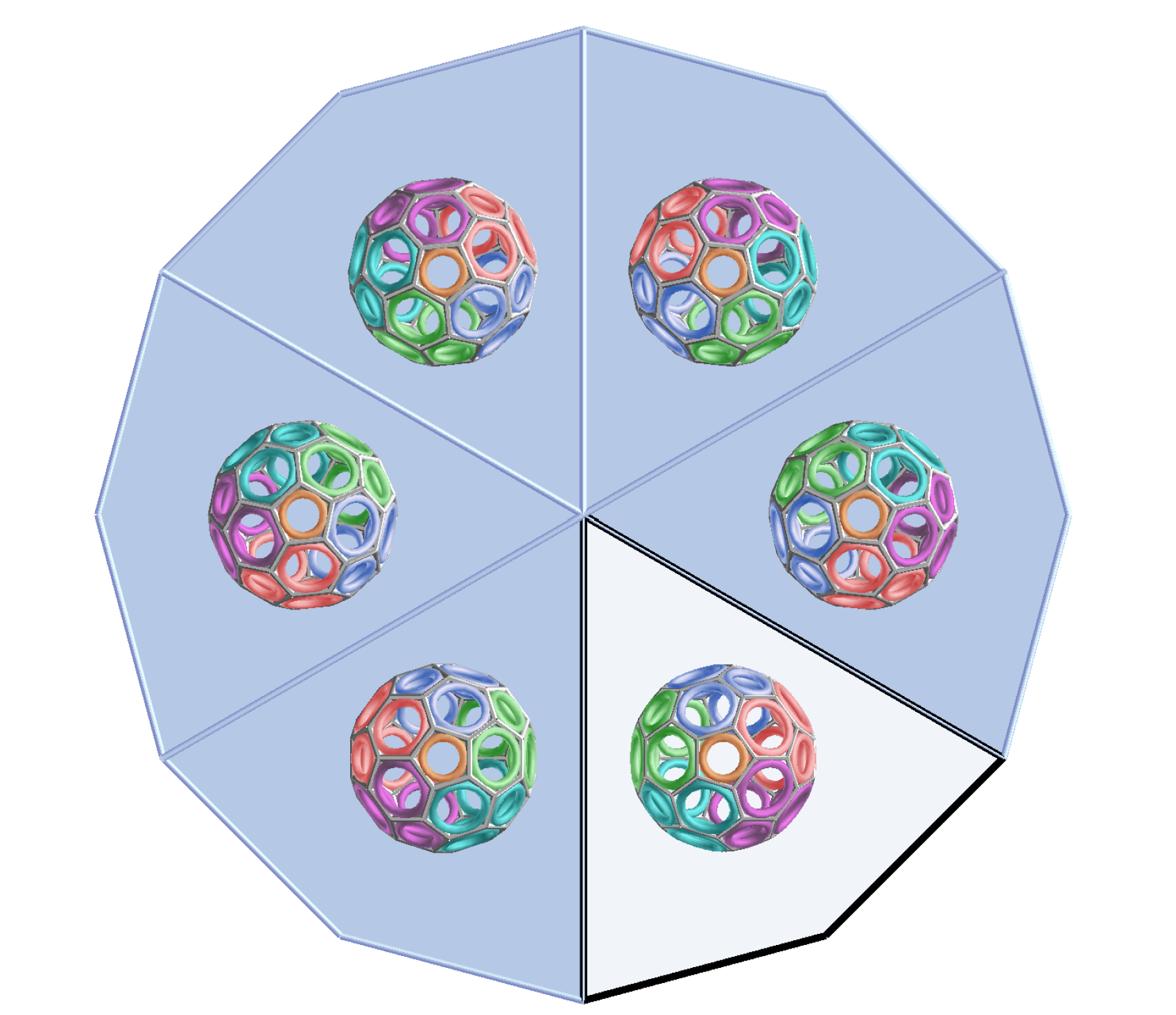
| Leonard Weydemann, Christian Clemenz, Clemens Preisinger (leonard.weydemann@uni-ak.ac.at, christian.clemenz@uni-ak.ac.at, clemens.preisinger@uni-ak.ac.at)
On the Structural Properties of Voronoi DiagramsA Voronoi diagram is a tessellation technique, which subdivides space into regions in proximity to a given set of objects called seeds. Patterns emerging naturally in biological processes (for example, in cell tissue) can be modelled in a biomimicry process via Voronoi diagrams. As they originate in nature, we investigate the physical properties of such patterns to determine whether they are optimal given the constraints imposed by surrounding geometry and natural forces. This paper describes under what circumstances the Voronoi tessellation has optimal (structural) properties by surveying recent studies that apply this tessellation technique across different scales. To investigate the properties of random and optimized Voronoi tessellations in comparison to a regular tessellation method, we additionally run and evaluate a simulation in Karamba3D, a parametric structural engineering tool for Rhinoceros3D. The novelty of this research lies in presenting a simple and straightforward simulation of Voronoi diagrams and highlighting how and where their advantages over regular tessellations can be exploited by surveying more advanced approaches as found in literature. Key words:
Voronoi diagrams, 3D tessellations, 3D scaffolds |
|
| Ana Katalenić, Aleksandra Čižmešija, Željka Milin Šipuš (akatalenic@foozos.hr, cizmesij@math.hr, zeljka.milin-sipus@math.hr)
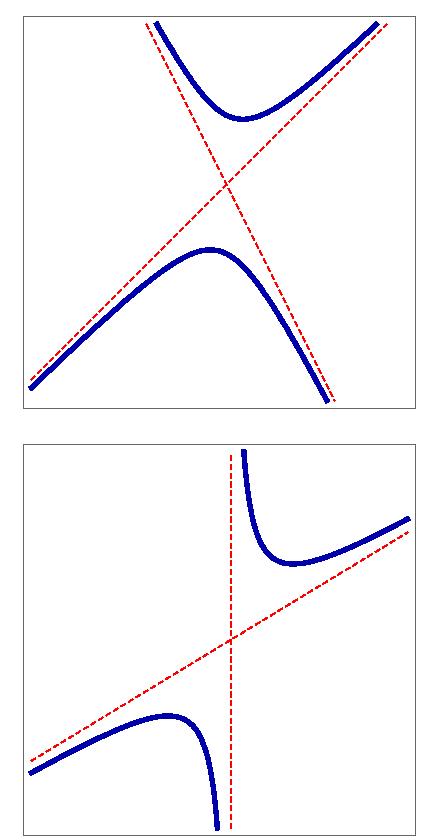
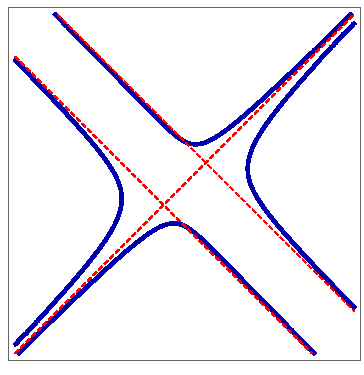
Asymptotes of Plane Curves – RevisitedIn this paper we present a review of the basic ideas and results concerning asymptotic lines of plane curves. We discuss their different definitions, namely that of a limiting position of tangent lines, of the tangent line at infinity, and finally the one that requires that the distance between points of a curve and asymptotic line tends to 0 as the point moves along an infinite branch of the curve. We also recall the method of determining asymptotes of algebraic curves from the leading coeffients in their equation and provide examples. Key words:
plane curve, asymptote, limiting tangent
line, tangent at inffnity |
|
| Christian Clemenz, Leonard Weydemann (christian.clemenz@uni-ak.ac.at, leonard.weydemann@uni-ak.ac.at)
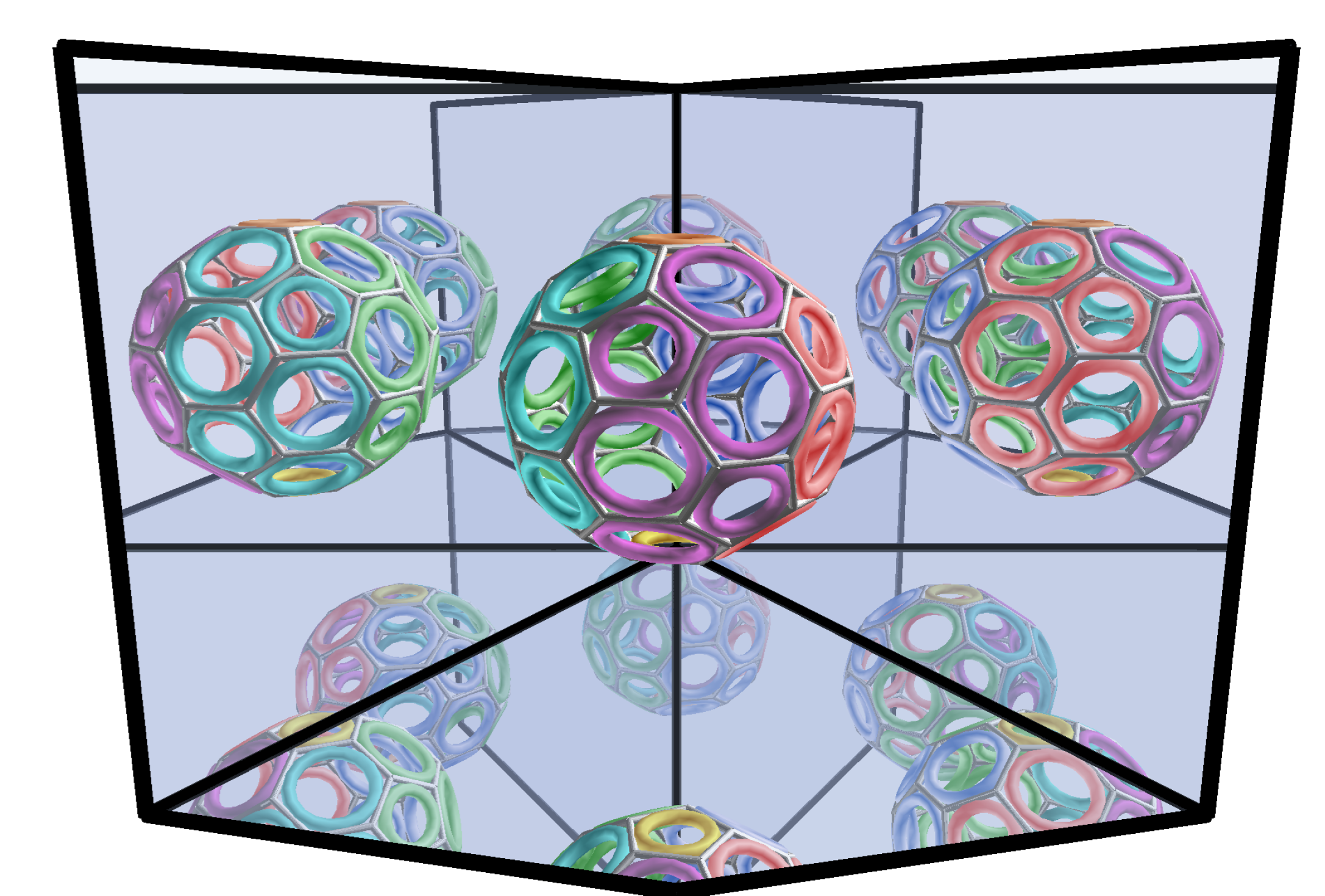
Reflection Techniques in Real-Time Computer GraphicsReflections have a long history in computer graphics, as they are important for conveying a sense of realism as well as depth and proportion. Their implementations come with a multitude of difficulties, and each solution typically has various trade-offs. Approaches highly depend on the geometry of the reflective surface since curved reflectors are usually more difficult to portray accurately. Techniques can typically be categorized by whether they work with the actual geometry of the reflected objects or with an image of these objects. For curved surfaces, image-based techniques are usually preferred, whereas for planar surfaces the reflected geometry can be used more easily because of the lack of distortion. With current advances in graphics hardware technology, ray tracing is also becoming more viable for real-time applications. Many modern solutions often combine multiple approaches to form a hybrid technique. In this paper, we give an overview of the techniques used in computer graphics applications to create real-time reflections. We highlight the trade-offs that have to be dealt with when choosing a particular technique, as well as their ability to produce interreflections. Finally, we describe how contemporary state-of-the-art rendering engines deal with reflections. Key words:
reflections, interreflections, real-time rendering |