 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
| Temel Ermiş, Özcan Gelişgen, Rustem Kaya(termis@ogu.edu.tr, gelisgen@ogu.tr, rkaya@ogu.edu.tr)
On Taxicab Incircle and Circumcircle of a TriangleIn this work, we study existence of taxicab incircle and cir-  Article in PDF. Article in PDF. |
| Ana Sliepčević, Ivana Božić (anas@grad.hr, ivana.bozic@tvz.hr)
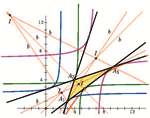
Steiner Curve in a Pencil of ParabolasUsing the facts from the theory of conics, two theorems
that are analogous to the theorems in triangle geometry
are proved. If the pencil of parabolas is given by three
lines a, b, c, it is proved that, the vertex tangents of all
the parabolas in the pencil, envelop the Steiner deltoid
curve δ, and the axes of all parabolas in the same pencil
envelop further deltoid curve α. Furthermore, the deltoid
curves are homeothetic. It is proved that all the vertices in
the same pencil of parabolas are located at the 4th degree
curve. The above mentioned curves are constructed and
treated by synthetic methods. |
|
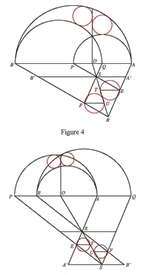
| Hiroshi Okumura (hiroshiokmr@gmail.com)
Ubiquitous Archimedean Circles of the Collinear ArbelosWe generalize the arbelos and its Archimedean circles, and
|
|
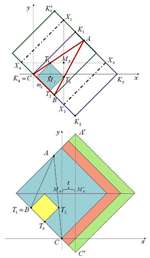
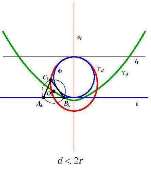
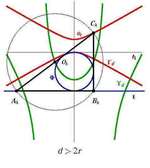
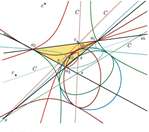
| Nikolina Kovačević, Ana Sliepčević (nkovacevic@rgn.hr, anas@grad.hr)
On the Certain Families of TrianglesIn the present paper, we study a set T={T(r,d) : d ∈R} |
|
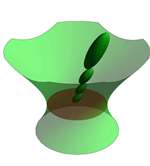
| Marijana Babić, Srđan Vukmirović (marijana@matf.bg.ac.rs, vsrdjan@matf.bg.ac.rs)
Central Projection of Hyperbolic Space onto a HorosphereHorosphere is surface in hyperbolic space that is isometric to the Euclidean plane. In order to correctly visualize
hyperbolic space we embed flat computer screen as horosphere and investigate geometry of central projection of
hyperbolic space onto horosphere. We also discuss realization of hyperbolic isometries. Corresponding algorithms
are implemented in Mathematica package L3toHorospere. |
|
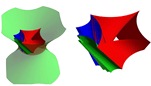
| János Pallagi, Benedek Schultz, Jenö Szirmai (jpallagi@math.bme.hu, schultz.benedek@gmail.com, szirmai@math.bme.hu)
On Regular Square Prism Tilings in ^SL2R Space (tilda)In [9] and [10] we have studied the regular prisms and prism
|
| Norman John Wildberger, Ali Alkhaldi (n.wildberger@unsw.edu.au, aalkaldy@hotmail.com)
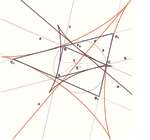
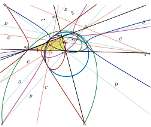
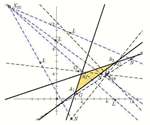
Universal Hyperbolic Geometry IV: Sydpoints and Twin CircumcirclesWe introduce the new notion of sydpoints into projective triangle geometry with respect to a general bilinear form. These are analogs of midpoints, and allow us to extend hyperbolic triangle geometry to non-classical triangles with points inside and outside of the null conic. Surprising analogs of ircumcircles may be defined, involving the appearance of pairs of twin circles, yielding in general eight circles with interesting intersection properties.Key words: universal hyperbolic geometry, triangle geo- metry, projective geometry, bilinear form, sydpoints, twin circumcircles  Article in PDF. Article in PDF. |
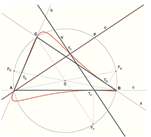
| Nguyen Le, Norman John Wildberger (n.h.le@unsw.edu.au, n.wildberger@unsw.edu.au)
AUniversal Affine Triangle Geometry and Four-fold Incenter SymmetryWe develop a generalized triangle geometry, using an ar- |
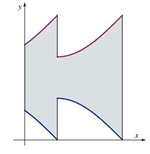
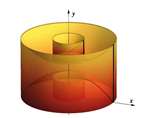
| Tatjana Slijepčević-Manger (tmanger@grad.hr)
The Volume of a Solid of RevolutionIn this paper we present classical methods (disk and shell |