 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
| Norman John Wildberger (n.wildberger@unsw.edu.au)
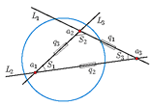
Univerzalna hiperbolička geometrija II: slikovni pregledČlanak pruža jednostavan slikovni uvod u univerzalnu u hiperboličku geometriju. Objašnjava se kako razumjeti sadržaj koristeći samo osnovnu projektivnu geometriju, proširenu jednom istaknutom kružnicom. Na taj se način dobiva potpuno algebarski okvir za hiperboličku geometriju, koji vrijedi nad poljem racionalnih brojeva (i u biti nad bilo kojim poljem karakteristike različite od 2) i daje mnoge nove lijepe teoreme. Ovi su rezultati prikazani crtežima u boji, a čitatelj je pozvan provjeriti ih konstruktivno i računski.Ključne riječi: hiperbolička geometrija, projektivna geometrija, racionalna geometrija, kvadranca, širina, kvadrea  Članak u PDF-u. Članak u PDF-u.
|
|
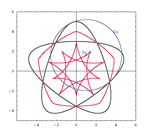
| Ana Sliepčević, Ema Jurkin (ejurkin@rgn.hr, anas@grad.hr)
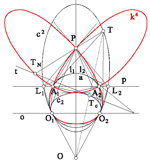
Puževi u hiperboličkoj ravniniDobro su poznata svojstva krivulje euklidske ravnine zvane Pascalov puž. U ovom se radu u hiperboličkoj ravnini konstruiraju krivulje sa sličnim svojstvima. Te su krivulje nazvane hiperboličkim puževima i definirane kao nožišne krivulje kružnica.Pokazuje se da su svi hiperbolički puževi cirkularne kvartike, a neke od njih su čak potpuno cirkularne. Ključne riječi: Pascalov puž, hiperbolička ravnina, potpuno cirkularne krivulje 4.reda  Članak u PDF-u. Članak u PDF-u. |
|
| Márta Szilvási-Nagy (szilvasi@math.bme.hu)
Dijelovi plohe konstruirani iz podataka o zakrivljenostiU ovom članku se prikazuje metoda za konstrukciju glatkih dijelova plohe koji odgovaraju mreži trokuta. Takav dio plohe može zamijeniti dobro definirano područje mreže, a može se upotrijebiti npr. retriangulaciji, simplifikaciji mreže i renderiranju.Ulazni podaci su procijenjene vrijednosti zakrivljenosti i glavni smjerovi izračunati iz kružne okoline određenog trokuta mreže. Ključne riječi: mreža trokuta, glavne zakrivljenosti, lokalna aproksimacija plohe  Članak u PDF-u. Članak u PDF-u. |
|
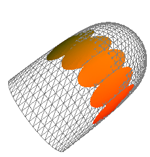
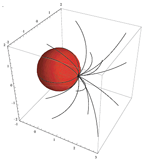
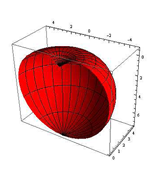
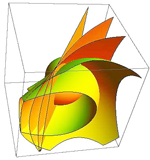
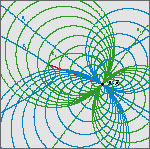
| János Pallagi, Benedek Schultz, Jenö Szirmai (jpallagi@math.bme.hu, schultz.benedek@gmail.com, szirmai@math.bme.hu) Vizualizacija geodetskih krivulja, sfera i ekvidistantnih ploha u prostoru S2×RS2×R geometrija izvodi se kao direktni produkt sferne ravnine S2 i realnog pravca R. U članku [9], treći je autor odredio geodetske krivulje i geodetske kugle prostora S2×R, izračunao njihov volumen i definirao pojam popunjavanja geodetskim kuglama i njegovu gustoću. Pored toga, razvio je metodu određivanja gustoće popunjavanja geodetskim kuglama za generalizirane Coxeterove grupe prostora S2×R i primijenio taj algoritam na njih.U [3] je E. MOLNAR pokazao da homogeni 3-prostori imaju jedinstvenu interpretaciju u projektivnim 3-sferama PS3(V4,V3,R). U našem članku koristit ćemo projektivni model S2×R geometrije te se na taj način geodetske linije i kugle mogu vizualizirati na euklidskom ekranu računala. Nadalje, definirat ćemo pojam plohe jednako udaljene od dviju točaka, odrediti njezinu jednadžbu te je vizualizirati u pojedinim slučajevima. Također ćemo pokazati mogući način pojednostavljena računa i dobiti jednadžbe plohe s točnijim geometrijskim značenjem. Slike su napravljene u Wolframovom programu Mathematica. Ključne riječi: neeuklidske geometrije, projektivna geometrija, geodetske sfere, ekvidistantne plohe  Članak u PDF-u. Članak u PDF-u. |
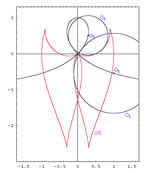
| Tibor Dósa (dosa.tibor@t-online.de)
Ekvidistantne, vlastito-ekvidistantne i svojstveno-ekvidistantne krivulje u euklidskoj ravniniU ravnini su dane dvije krivulje. Tražimo krivulju koja je od njih jednako udaljena u sljedećem smislu: što je geometrijskomjesto središta kružnica koje diraju obje dane krivulje? Te točke su jednako udaljene od dviju danih krivulja. Vlastito-ekvidistantna krivulja dane krivulje je geometrijsko mjesto središta onih kružnica koje danu krivulju dodiruju dva puta. Svojstveno-ekvidistantna krivulja dane krivulje je anvelopa kružnica koje diraju danu krivulju, a njihova središta također leže na toj krivulji. Također se proučava i obrnuti problem, dane su krivulje c1 i ce. Koja je krivulja c2 tako da je ce ekvidistantna krivulja za c1 i c2? O ovim krivuljama se malo zna, npr. [3], [4], [5], možda zbog toga što njihovo izračunavanje zahtijeva efikasni algebarski program. Proučavali smo samo krivulje čije su jednadžbe polinomi sa cjelobrojnim koeficijentima u euklidskoj ravnini. Koristili smo program Mathematica 5.2. Ključne riječi: ekvidistantna krivulja  Članak u PDF-u. Članak u PDF-u. |
|
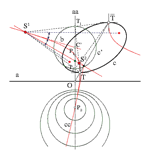
| Sonja Gorjanc, Tibor Schwarcz, Miklós Hoffman (sgorjanc@grad.hr, schwartz@inf.unideb.hu, hofi@ektf.hu)
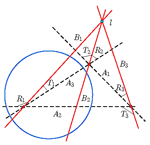
O perspektivnim kolineacijama koje danu koniku preslikavaju u kružniceU članku je dokazano da središta svih perspektivnih kolineacija koje s obzirom na zadanu os preslikavaju danu koniku c u kružnicu, leže na jednoj konici cc konfokalnoj s početnom konikom. Konike c i cc imaju realna sjecišta, a njihova zajednička dijametralna tetiva konjugirana je smjeru zadane osi kolineacije.Nadalje je dokazano da osi svih prespektivnih kolineacija koje s obzirom na zadano središte S preslikavaju danu koniku c u kružnicu, čine dva pramena paralelnih pravaca. Smjerovi tih pramenova konjugirani su zajedničkim dijametralnim tetivama konike c i njoj konfokalne konike koja sadrži točku S i realno siječe c. Na kraju je formuliran teorem koji govori o vezi para konfokalnih konika i temeljnih elemenata perspektivnih kolineacija koje te konike preslikavaju u kružnice. Ključne riječi: perspektivna kolineacija, konfokalne konike, Apolonijeve kružnice  Članak u PDF-u. Članak u PDF-u. |