Znanstveno-stručni časopis
Hrvatskog društva za geometriju i grafiku

Scientific and Professional Journal
of the Croatian Society for Geometry and Graphics





Norman John Wildberger (n.wildberger@unsw.edu.au)

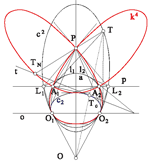
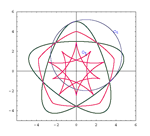
Universal Hyperbolic Geometry II: A pictorial overview

This article provides a simple pictorial introduction to universal hyperbolic geometry. We explain how to understand the subject using only elementary projective geometry, augmented by a distinguished circle. This provides a completely algebraic framework for hyperbolic geometry, valid over the rational numbers (and indeed any field not of characteristic two), and gives us many new and beautiful theorems. These results are accurately illustrated with colour diagrams, and the reader is invited to check them with ruler constructions and measurements.

Key words: hyperbolic geometry, projective geometry, rational trigonometry, quadrance, spread, quadrea


Article in PDF.

 







Ana Sliepčević, Ema Jurkin (ejurkin@rgn.hr, anas@grad.hr)

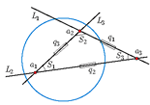
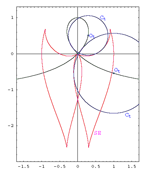
Snails in Hyperbolic Plane

The properties of the limacon of Pascal in the Euclidean plane are well known. The aim of this paper is to obtain the curves in the hyperbolic plane having the similar properties. That curves are named hyperbolic snails and defined as the circle pedal curves.
It is shown that all of them are circular quartics, while
some of them are entirely circular.

Key words: limacon of Pascal, hyperbolic plane, entirely circular 4-order curves

Article in PDF.



Márta Szilvási-Nagy (szilvasi@math.bme.hu)

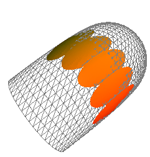
Surface Patches Constructed from Curvature Data

In this paper a technique for the construction of smooth surface patches fitted on triangle meshes is presented. Such a surface patch may replace a well defined region of the mesh, and can be used e.g. in retriangulation, mesh-simplification and rendering.
The input data are estimated curvature values and principal directions computed from a circular neighborhood of a specified triangle face of the mesh.


Key words: triangle mesh, principal curvatures, local surface approximation

Article in PDF.

 


János Pallagi, Benedek Schultz, Jenö Szirmai (jpallagi@math.bme.hu, schultz.benedek@gmail.com, szirmai@math.bme.hu)

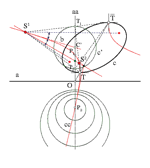
Visualization of Geodesic Curves, Spheres and Equidistant Surfaces in S^2×R Space

The S2×R geometry is derived by direct product of the spherical plane S2 and the real line R. In [9] the third author has etermined the geodesic curves, geodesic balls of S2×R space, computed their volume and defined the notion of the geodesic ball packing and its density. Moreover, he has developed a procedure to determine the density of the geodesic ball packing for generalized Coxeter space groups of S2×R and applied this algorithm to them.
E. MOLNÁR showed in [3], that the homogeneous 3-spaces have a unified interpretation in the projective 3-sphere
PS3(V4,V3, R). In our work we shall use this projective model of S2×Rgeometry and in this manner the geodesic lines, geodesic spheres can be visualized on the Euclidean screen of omputer.
Furthermore, we shall define the notion of the equidistant surface to two points, determine its equation and visualize it in some cases. We shall also show a possible way of making the computation simpler and obtain the equation of an equidistant surface with more possible geometric meaning. The pictures were made by the Wolfram Mathematica software.

Key words: non-Euclidean geometries, projective geometry, geodesic sphere, equidistant surface
Article in PDF.

 

 

Tibor Dósa (dosa.tibor@t-online.de)

Equidistant-, Own-Equidistant- and Self-Equidistant-Curves in the Euclidean Plane

There are given two curves in the plane. We are looking for the equidistant-curve of both in the following sense: what is the geometric locus of the centers of the circles that are tangent to both given curves? These points are in the same distance from the two given curves. The own-equidistant curve of a given curve is the locus of the centers of the circles that are twice tangent to the curve.
The self-equidistant curve of a given curve is the envelope curve of the circles that are tangent to the curve and their centers lay on the curve too. The inverse problem is inspected too, curves c1 and ce are given. Which is the curve c2 so that ce is the equidistant-curve of c1 and c2?
About these curves few is known [3], [4], [5], perhaps because
one needs for their calculation an efficient computer algebra program. We have investigated only curves of polinomial equation with coefficients of integer numbers in the Euclidean plane. We have used the computer program Mathematica 5.2.


Key words: equidistant curve

Article in PDF.


Sonja Gorjanc, Tibor Schwarcz, Miklós Hoffman (sgorjanc@grad.hr, schwartz@inf.unideb.hu, hofi@ektf.hu)

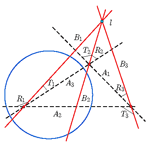
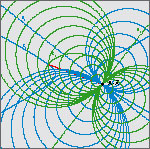
On Central Collineations which Transform a Given Conic to a Circle

In this paper we prove that for a given axis the centers of all central collineations which transform a given proper conic c into a circle, lie on one conic cc confocal to the original one. The conics c and cc intersect into real points and their common diametral chord is conjugate to the direction of the given axis.
Furthermore, for a given center S the axes of all central collineations that transform conic c into a circle form two pencils of parallel lines. The directions of these pencils are conjugate to two common diametral chords of c and the confocal conic through S that cuts c at real points.
Finally, we formulate a theorem about the connection of the pair of confocal conics and the fundamental elements of central collineations that transform these conics into circles.

Key words: central collineation, confocal conic,; Apollonian circles

Article in PDF.