 |
Znanstveno-stručni
časopis Hrvatskog društva za geometriju i grafiku Scientific and Professional Journal |
|
|
Konstantinos Myrianthis, Hellmuth Stachel (myrian@ath.forthnet.gr, stachel@dmg.tuwien.ac.at)
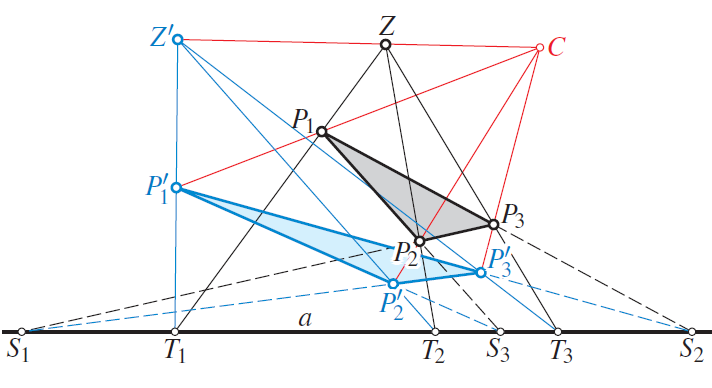
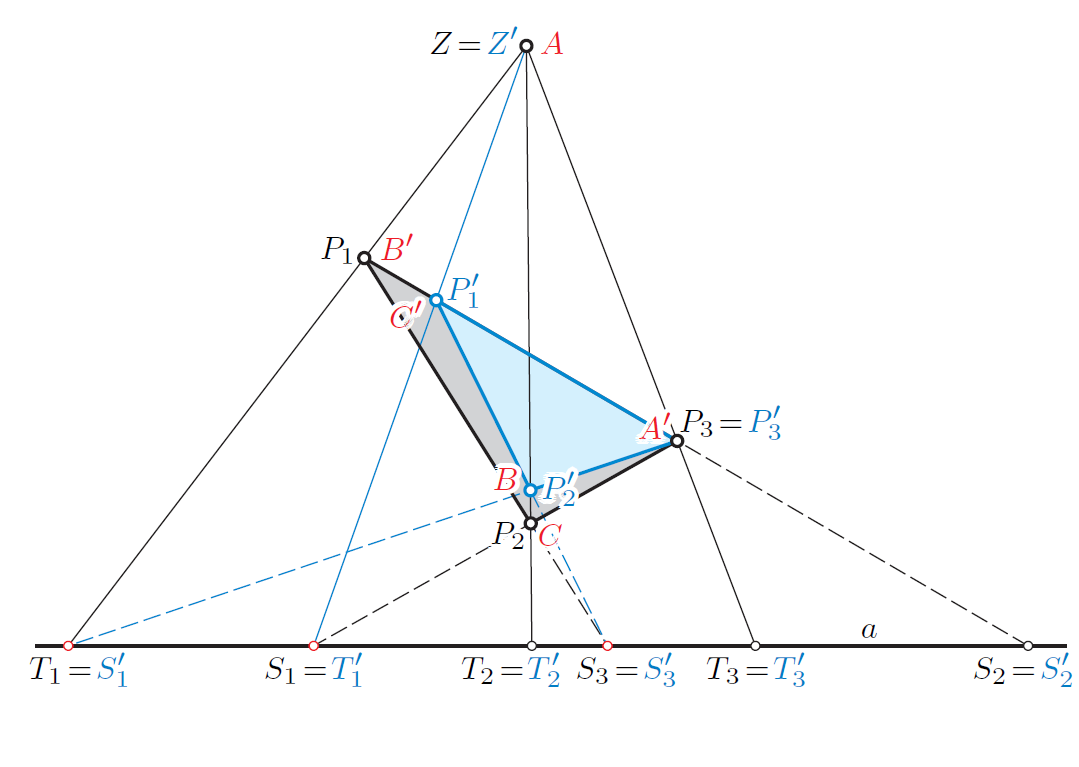
On Permutations of Desarguesian SextuplesDesargues's theorem plays an essential role at the axiomatic foundations of Projective Geometry. The configuration behind this theorem contains ten lines, the sides of
two triangles, three lines through the center and the axis.
We focus on the ordered sextuple of intersection points
with the axis and call it Desarguesian. A permutation of
this sextuple is called admissible if it preserves the property
of being Desarguesian. Some permutations are admissible
only if Pappus's theorem holds in the plane. Under this
assumption we can prove that for each permutation there
exist particular Desarguesian sextuples which remain Desarguesian under the permutation.
 Article in PDF. Article in PDF. |
|
| Gunter Weiss, Boris Odehnal (boris.odehnal@uni-ak.ac.at, weissgunter@gmx.at)
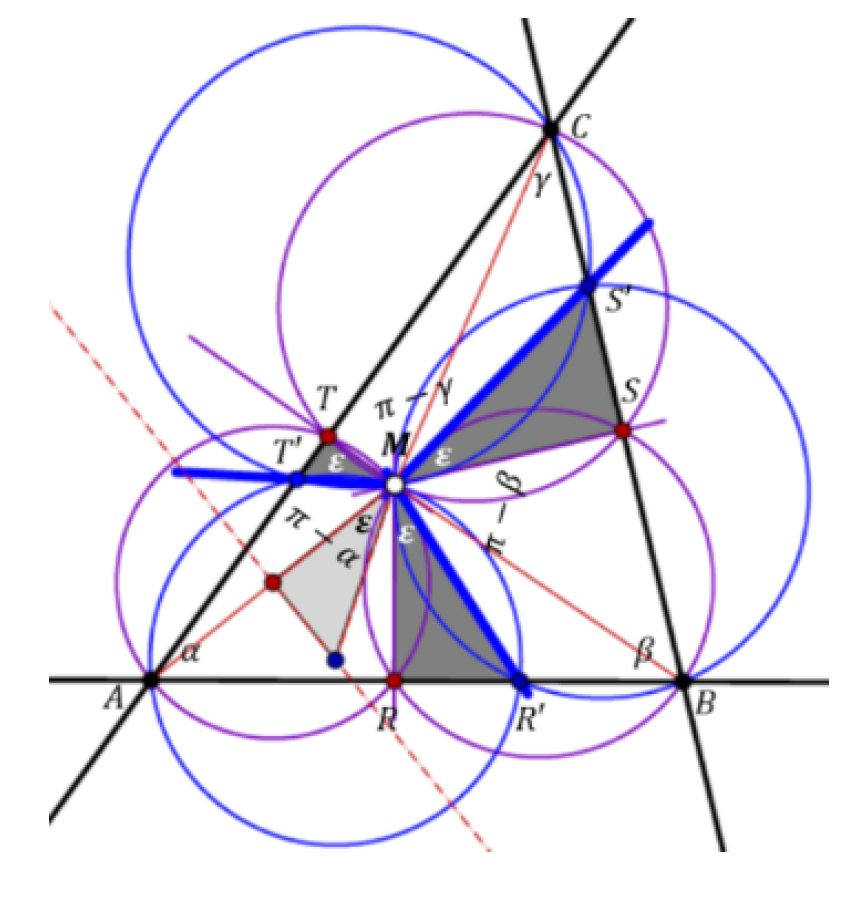
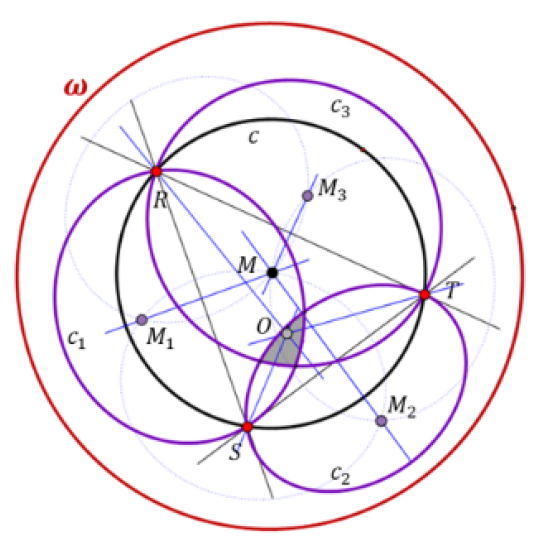
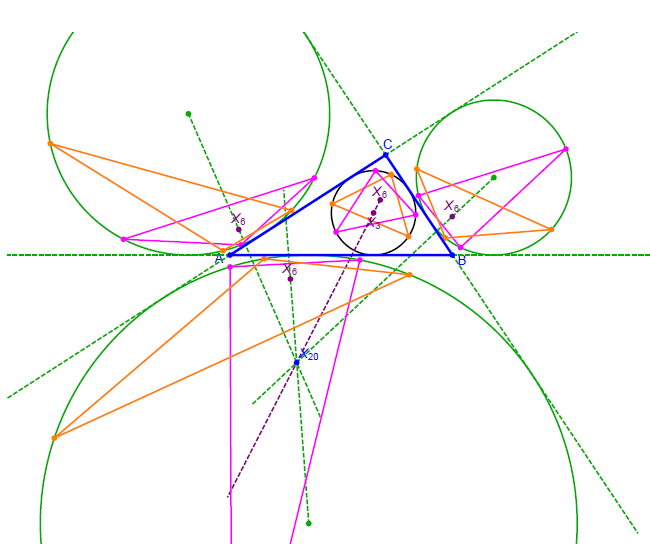
Miquel's Theorem and its Elementary Geometric RelativesThe elementary geometric Miquel theorem concerns a triangle
ΔABC and points R, S, T on its sides, and it states
that the circles k(ART), k(BRS), k(CST) have a common
point M, the Miquel point to these givens. Choosing R, S,
T in special ways one receives the so-called beermat theorem, the
Brocard theorems, and the Steiner Simson-Wallace
theorem as special cases of Miquel's theorem. Hereby facts
connected with Brocard's theorem follow from properties
of Miquel's theorem. If e.g. R, S, T fulfill the Ceva condition, Miquel's construction induces a mapping of the Ceva
point to the Miquel point. We discuss this and other mappings, which are natural consequences of Miquel's theorem.
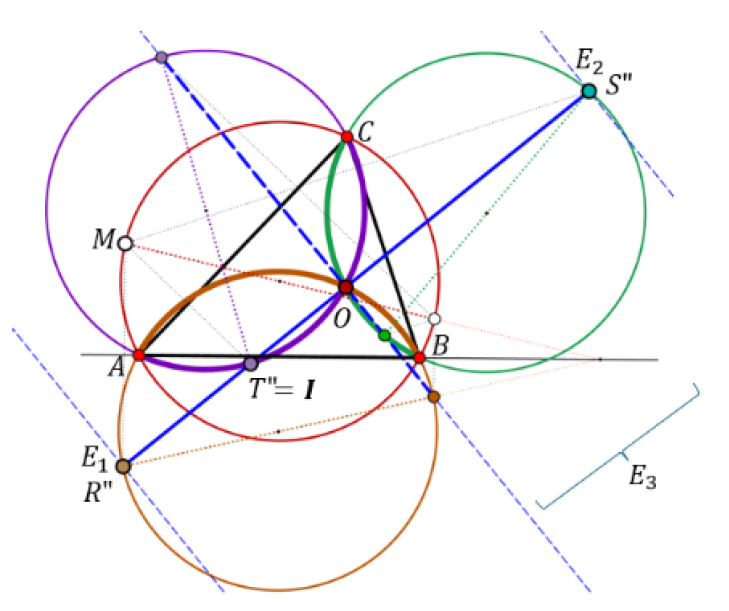
Furthermore, if the points R, S, T run through the sides
of Δ such that e.g. the affine ratios ar(ARB), ar(BSC),
ar(CTA) are equal, then the corresponding Miquel points
M run through the circumcircle of the triangle formed by
the Brocard points and the circumcenter of Δ. Besides
these three remarkable points of Δ, this circle contains
several other triangle centers. Even though most of the
presented topics are well-known, their mutual connections
seem to be not yet considered in standard references on
triangle geometry and therefore might justify an additional
treatment. |
|
| Boris Odehnal (boris.odehnal@uni-ak.ac.at)
Universal Porisms and Yff ConicsThe Yff circumellipse and the Yff inellipse of a triangle allow for a poristic family of triangles (henceforth called Yff porism), since the initial triangle is already an interscribed triangle. Surprisingly, the Yff porism can be parametrized by means of rational functions, and thus, it delivers a porism in Universal Geometry. This also allows us to give explicit examples of poristic triangle families over finite fields. Considering the Yff inellipse and Yff circumellipse as the basis of an exponential pencil of conics, we can iterate the construction of the porism and find an infinite sequence (and thus infinitely many) nested rational triangle porisms over the real (and complex) number field or a finite closed chain of porisms in the case of a finite field. Key words: porism, inellipse, circumellipse, triangle, rational
porism, rational parametrization, finite field, finite
projective plane |
|
| Dominique Laurain, Peter Moses, Dan Reznik
(dominique.laurain31@orange.fr, moparmatic@gmail.com, dreznik@gmail.com)
Cramer-Castillon on a Triangle’s Incircle and ExcirclesThe Cramer-Castillon problem (CCP) consists in finding
one or more polygons inscribed in a circle such that their
sides pass cyclically through a list of N points. We study
this problem where the points are the vertices of a triangle
and the circle is either the incircle or one of the excircles.
We find that (i) in each case there is always a pair of solutions (total of 8 new triangles and 24 vertices); (ii) each
pair shares all Brocard geometry objects, (iii) barycentric
coordinates are laden with the golden ratio; and (iv) simple
operations on the barycentrics of a single vertex out of the
24 yield all other 23. |
|
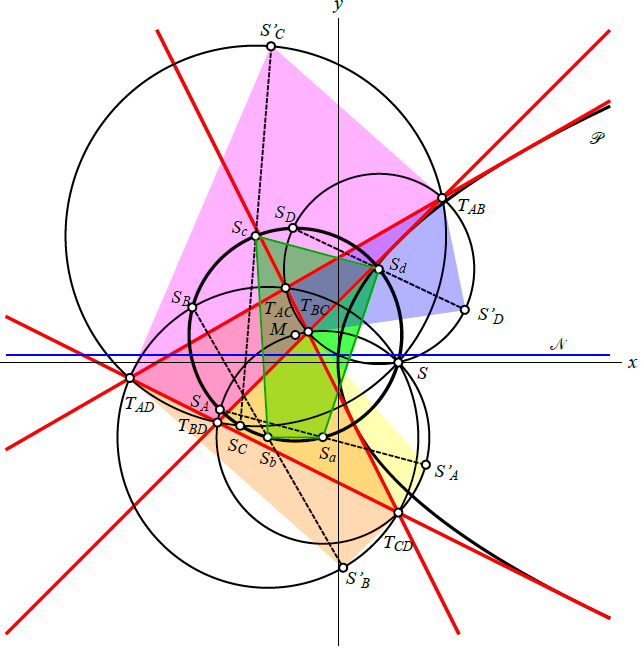
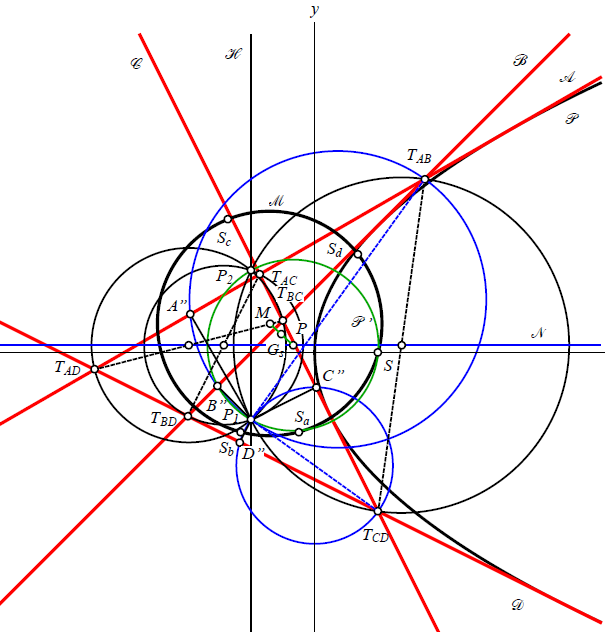
| Vladimir Volenec, Ema Jurkin, Marija Šimić Horvath (volenec@math.hr, ema.jurkin@rgn.unizg.hr, marija.simic@arhitekt.hr)
A Complete Quadrilateral in Rectangular Coordinates IIThis paper is a continuation of research on a geometry of a complete quadrilateral in the Euclidean plane. We present the well-known facts on the complete quadrilateral but all proved in the same way by using rectangular coordinates, symmetrically on all four sides of the quadrilateral with four parameters a, b, c, d. The properties related to the central circle, orthopolar circle, Hervey's circle, Kantor's point and Plücker's points are observed. During this study, some new results come up. Key words:
complete quadrilateral, central circle, orthopolar
circle, Hervey's circle, Kantor's point, Plücker's points |
|
| Andrej Novak, Martina Armanda (andrej.novak@phy.hr, marty4arm@gmail.com)
The Application of the Cahn-Hilliard Equation for Digital Image InpaintingeWe investigate the application of the Cahn-Hilliard (CH) equation for digital image inpainting, focusing on various choices of nonlinear potential, including the double well potential and classifiers based on shock filters. These potentials are crucial in shaping the inpainting results, and their selection depends on the characteristics of specific images and the desired properties of reconstruction. Additionally, we present a numerical scheme based on the principle of convexity splitting, and we demonstrate the results of inpainting simple binary shapes. Throughout the text, we emphasize the fundamental features of the Cahn-Hilliard equation to enable a better understanding of the role of partial differential equations in image processing. Key words:
Cahn-Hilliard equation, digital image inpainting, numerical methods, image processing |