Gaussov postupak eliminacije je metoda rješavanja sustava linearnih algebarskih jednadžbi. Ideja je sljedeća. Operacijama, koje smo gore naveli, zadani sustav svesti na njemu ekvivalentan, tako da iz dobivenog sustava lako nađemo skup svih rješenja.
Neka je zadan sustav 1.4. Premjestimo jednadžbe u
sustavu, ako je potrebno, tako da koeficijent uz ![]() u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz
u prvoj
jednadžbi bude različit od nule. Zatim prvu jednadžbu podijelimo s
koeficijentom uz ![]() pomnožimo brojem koji je suprotan
koeficijentu uz
pomnožimo brojem koji je suprotan
koeficijentu uz ![]() u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz
u drugoj jednadžbi, i dodamo je drugoj
jednadžbi, zatim prvu jednadžbu podijelimo s koeficijentom uz ![]() pomnožimo brojem koji je suprotan koeficijentu uz
pomnožimo brojem koji je suprotan koeficijentu uz ![]() u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz
u trećoj
jednadžbi, i dodamo je trećoj jednadžbi, zatim prvu jednadžbu
podijelimo s koeficijentom uz ![]() pomnožimo brojem koji je
suprotan koeficijentu uz
pomnožimo brojem koji je
suprotan koeficijentu uz ![]() u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili
u četvrtoj jednadžbi, i dodamo je
četvrtoj jednadžbi, i t.d. Na taj način smo izbacili ![]() iz
druge, treće,
iz
druge, treće, ![]()
![]() -te jednadžbe i došli do ekvivalentnog
sustava oblika
-te jednadžbe i došli do ekvivalentnog
sustava oblika
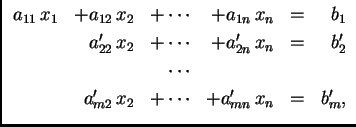
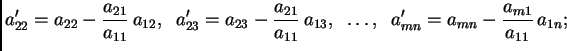
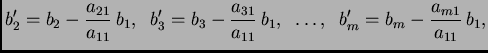
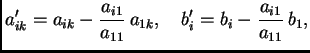 za
za Dakle ideja Gaussove metode eliminacije se sastoji u tome da se pomoću operacija 1.2.1 izbace nepoznanice koje se nalaze ispod ``glavne dijagonale''.
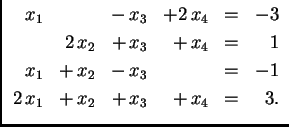
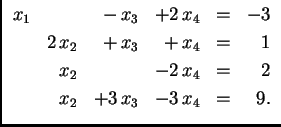
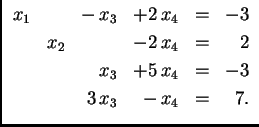
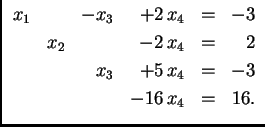
Metodu eliminacije možemo upotrebiti i nakon svođenja na ``trokutasti'' oblik da bismo izbacili nepoznanice iznad ``glavne dijagonale'' i došli tako do ``dijagonalnog'' oblika. Ta metoda se zove Gauss-Jordanova metoda. Na sljedećem primjeru pokažimo kako funkcionira ta metoda.
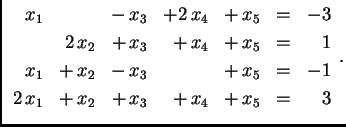
![% latex2html id marker 31176
$\displaystyle \begin{array}{rrrrrrr}
x_1 & & -\,x...
... +\,x_5 & = & -3 \\ [2mm]
& & & x_4 &+\frac{1}{4}\,x_5 & = & -1
\end{array}.$](img385.png)
![% latex2html id marker 31180
$\displaystyle \begin{array}{rrrrrrr}
x_1 & & -\,x...
...{4}\,x_5 & = & 2 \\ [2mm]
& & & x_4 &+\frac{1}{4}\,x_5 & = & -1
\end{array}.$](img387.png)
![% latex2html id marker 31182
$\displaystyle \begin{array}{rrrrrrr}
x_1 & & & &+...
...{4}\,x_5 & = & 2 \\ [2mm]
& & & x_4 &+\frac{1}{4}\,x_5 & = & -1
\end{array}.$](img388.png)
U ovom primjeru se pojavljuje ![]() kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za
kao neodređeni parametar. Tako
smo dobili mnogo rješenja, jer uzimajući za ![]() pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja.
pojedine brojeve,
nakon uvrštavanja dobivamo konkretna rješenja. ![]() može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.
može biti bilo
koji realan broj, pa tako imamo beskonačno mnogo rješenja. Zbog toga
što se u rješenju pojavljuje jedan neodređeni parametar, kažemo da
sustav ima jednoparametarski skup
rješenja.