Cijeli brojevi

Za zapisivanje brojeva općenito, pa i u kompjuteru, koristi se niz znamenaka u nekom brojevnom sustavu. U tu svrhu treba odrediti bazu $\beta.$ Na pr. u dekadskom sustavu je $\beta=10,$ a u binarnom $\beta=2.$ Računati ne možemo s beskonačno mnogo znamenaka. To ne može niti kompjuter. Dapače, on je ograničen svojim fizičkim mogućnostima, hardwareom. Ograničenje se odnosi na broj znamenaka $p$ koje može upotrebiti za zapis jednog broja. Broj $p$ se zove preciznost. Uređeni par $(\beta,p)$ zove se format.

Cijeli brojevi se u kompjuteru zapisuju u formatu $(2,16)$ ili $(2,32).$ Dakle radi se o brojevima koji se zapisuju pomoću znamenki 0 i $1$ razmještenih na $16$ ili $32$ mjesta. Pri tom se prvo mjesto koristi za predznak. Broj 0 označava pozitivan broj, $1$ negativan. Pojedino mjesto na koje možemo upisati jednu znamenku zove se bit.

Imamo sljedeći algoritam za pretvaranje broja zapisanog u dekadskom sustavu u binarni.

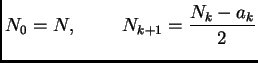Algoritam 11   Neka je $N$ dekadski zapis broja. Računamo

$$N_0 = N,\hspace{1cm}N_{k+1} = \frac{N_k-a_k}{2}$$    za $$k=0,1,2,\ldots{},$$

gdje je

$$a_k = \left\{ \begin{array}{ll} 1,... ...ako je $N_k$ neparan}, \\ 0, & \text{ako je $N_k$ paran}. \end{array}\right.$$

Račun provodimo sve dok ne dobijemo $N_k=0.$

Primjer 3.23   Treba za broj koji ima dekadski zapis $1998$ naći binarni zapis.

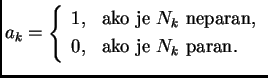
Rješenje.

$k$	0	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$	$10$
$N_k$	$1998$	$999$	$499$	$249$	$124$	$62$	$31$	$15$	$7$	$3$	$1$
$a_k$	0	$1$	$1$	$1$	0	0	$1$	$1$	$1$	$1$	$1$

Dakle binarni zapis je $11111001110.$

Tako se u formatu $(2,16)$ dekadski broj $1998$ zapisuje kao

$$0000011111001110.$$

Segment određen donjom i gornjom granicom zapisa zove se rang. Budući da u formatu $(2,16)$ imamo $15$ bitova za upis znamenaka (jedan bit je rezerviran za predznak), i budući da se mogu koristiti samo znamenke 0 i $1,$ najveći broj koji tako možemo zapisati je

$$111111111111111 = 2^{14} + 2^{13} + \cdots + 2^1 + 2^0 = \frac{2^{15}-1}{2-1} = 2^{15}-1 = 32767.$$

Najmanji cijeli broj koji se tako može zapisati je $-32768.$ Tako je rang u ovom slučaju

$$[-32768,32767].$$

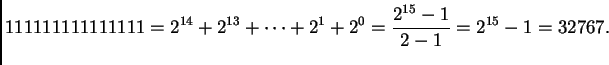
Ovakav zapis brojeva se zove zapis pomoću fiksnog zareza (fixed-point). U aritmetici fiksnog zareza postoje greške, no mi ćemo se ovdje ograničiti samo na neke aspekte pojave grešaka kod zapisa i računanja s realnim brojevima.