




Next: Metoda konačnih elemenata
Up: Varijacijske metode
Previous: Varijacijske metode
Sadržaj
Indeks
Ritzova metoda
Pogledajmo kako ona funkcionira kad se radi o rubnom
problemu
Kao u jednodimenzionalnom slučaju izaberemo 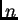 linearno nezavisnih
funkcija
linearno nezavisnih
funkcija
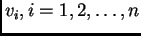 koje zadovoljavaju rubni
uvjet. Rješenje se pretpostavi u obliku
i neodređeni koeficijenti se odrede
iz uvjeta da
koje zadovoljavaju rubni
uvjet. Rješenje se pretpostavi u obliku
i neodređeni koeficijenti se odrede
iz uvjeta da 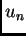 minimizira pripadni funkcional energije
Tako dobiveni
minimizira pripadni funkcional energije
Tako dobiveni 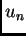 leži u vektorskom prostoru razapetom s
funkcijama
leži u vektorskom prostoru razapetom s
funkcijama 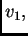
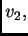
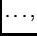
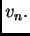 Rješenje ne mora ležati u tom
prostoru, pa u tom slučaju
Rješenje ne mora ležati u tom
prostoru, pa u tom slučaju 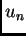 nije točno već samo približno
rješenje. No, što veći
nije točno već samo približno
rješenje. No, što veći 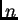 uzmemo, to je manja greška koju činimo
prihvaćajući
uzmemo, to je manja greška koju činimo
prihvaćajući 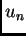 kao rješenje problema.
kao rješenje problema.
Prvi problem s kojim se susrećemo kod Ritzove metode je određivanje
funkcija 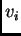 koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije
koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije 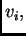 pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
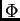 je derivabilna funkcija od
je derivabilna funkcija od 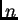 varijabli
varijabli
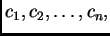 pa jednadžbe
za
pa jednadžbe
za
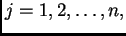 predstavljaju nužan uvjet za ekstrem funkcije
predstavljaju nužan uvjet za ekstrem funkcije
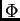 u točki
u točki
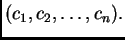 Ovo je sustav od
Ovo je sustav od 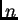 linearnih algebarskih
jednadžbi od
linearnih algebarskih
jednadžbi od 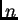 nepoznanica. Stavimo
Sada se sustav može kratko zapisati
gdje je
nepoznanica. Stavimo
Sada se sustav može kratko zapisati
gdje je
![$ K=[K_{ij}],\boldsymbol{c}=[c_j],\boldsymbol{b}=[b_i].$](img3531.png)
Nedostaci ove metode su u tome što je za proizvoljno područje teško
naći funkcije 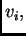 i u tome što je matrica
i u tome što je matrica 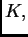 koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.





Next: Metoda konačnih elemenata
Up: Varijacijske metode
Previous: Varijacijske metode
Sadržaj
Indeks
2001-10-26


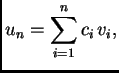
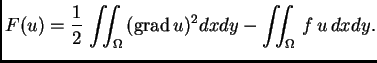
![]() koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije
koje moraju zadovoljavati rubni uvjet. Ako područje
nije dovoljno lijepo, mogu nastati problemi. Nakon što smo izabrali
funkcije ![]() pretpostavljeno rješenje uvrstimo u funkcional
pretpostavljeno rješenje uvrstimo u funkcional
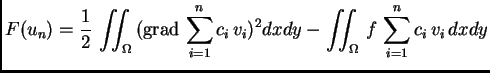
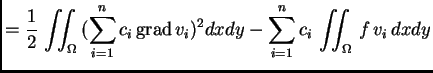
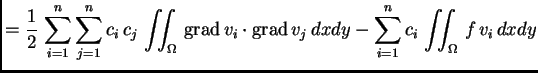
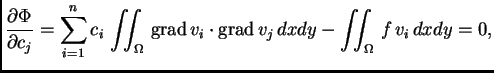
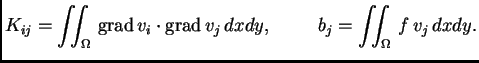
![]() i u tome što je matrica
i u tome što je matrica ![]() koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.
koja
se inače zove matrica krutosti, puna matrica, tj. općenito
je svaki njezin element različit od nule.