




Next: Jacobijeva metoda
Up: Iterativne metode
Previous: Iterativne metode
Sadržaj
Indeks
Želimo riješiti sustav linearnih algebarskih jednadžbi
Primijetite da je broj jednadžbi jednak broju nepoznanica.
Matrično
zapisan on glasi
gdje je
To je matrična jednadžba, i mi ćemo često o sustavu jednadžbi
govoriti kao o jednadžbi, misleći na ovu matričnu
jednadžbu. Pretpostavimo da je 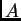 regularna matrica. Tada jednadžba ima
rješenje, i označimo to rješenje sa
regularna matrica. Tada jednadžba ima
rješenje, i označimo to rješenje sa
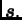
Osnovna ideja iterativnih metoda se sastoji u sljedećem. Stavimo
gdje su 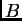 i
i 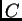 također kvadratne matrice
također kvadratne matrice 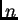 -tog reda. Jednadžbu
tada možemo prepisati kao
Ako s
-tog reda. Jednadžbu
tada možemo prepisati kao
Ako s
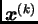 označimo
označimo 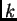 -tu aproksimaciju rješenja,
onda pomoću formule
možemo naći
-tu aproksimaciju rješenja,
onda pomoću formule
možemo naći 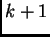 -vu aproksimaciju
rješenja.
-vu aproksimaciju
rješenja.
Naravno, da bi postupak uopće krenuo, treba biti zadana početna
aproksimacija
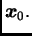 Nadalje, matrica
Nadalje, matrica 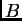 mora biti
regularna i relativno jednostavna, da bismo
mora biti
regularna i relativno jednostavna, da bismo
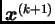 mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
Opišimo sada neke od iterativnih metoda.





Next: Jacobijeva metoda
Up: Iterativne metode
Previous: Iterativne metode
Sadržaj
Indeks
2001-10-26
![\begin{displaymath}
% latex2html id marker 38553
A = \left[
\begin{array}{cccc}...
...ray}{c}
x_1 \\ x_2 \\ \vdots \\ x_n
\end{array}
\right].\end{displaymath}](img2682.png)
![]() Nadalje, matrica
Nadalje, matrica ![]() mora biti
regularna i relativno jednostavna, da bismo
mora biti
regularna i relativno jednostavna, da bismo
![]() mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da
mogli relativno jednostavno izračunati. Također postupak nas mora
približavati k rješenju, tj. postupak mora biti takav da